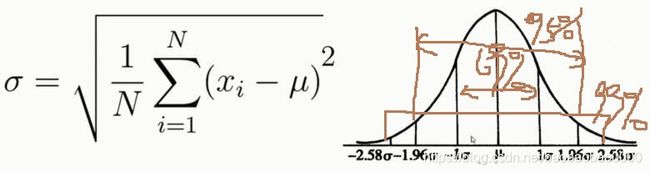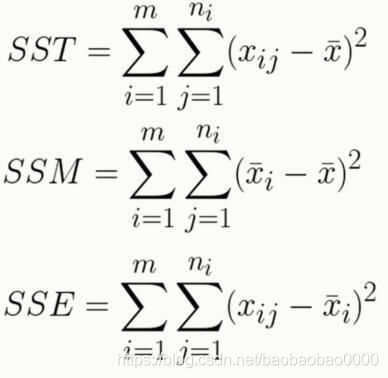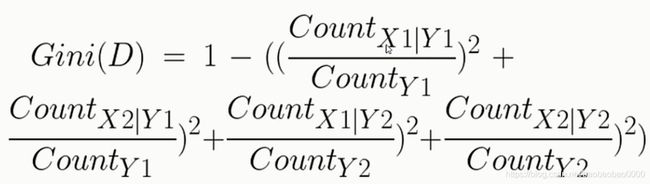Python数据分析理论与实战完整版本

一、Python数据分析初探

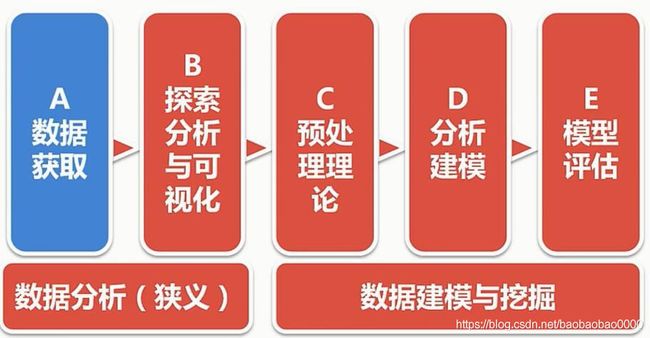
本次我们将从以上路线学习数据分析，本次课程使用python 3 编码学习。另外本章节学习所用的数据集可以kaggle上搜索HR.csv即可获得。

Python这门语言是Guido van Rossum在1989圣诞暑假研究出来的一门语言。特点是：简洁，开发效率高，运算速度慢，胶水特性。

二、数据获取

2.1 数据获取的手段

1.数据仓库
2.监测和抓取
3.填写、日志、埋点
4.计算

2.2 数据仓库

什么是数据仓库？
比如我们建立一个买书的网站，我们要建一个数据库存储各个用户信息，书籍信息，根据用户注册购买等行为，整个网站就运行起来了。网站发展很好，规模不断扩大，网站发展的方向就是一个问题。比如接下来该买什么数，给相应的用户推荐他需要的书。这就需要进行分析，数据分析仅仅依靠我们的数据库是不够的。我们需要一个东西把用户交互数据的变动信息记录下来，如记录某用户在几时几分几秒浏览的哪个页面，购买了什么书之类的。文件和日志也能完成这个记录但是不方面查找、比较和抽取特征等操作。所以我们需要一个载体记录业务流程中的每个细节，这就是数据仓库了。

将所有业务数据经汇总处理，构成数据仓库（DW）
1.全部实施的纪录
2.部分维度与数据的整理（数据集市-DM）
数据库 VS 仓库
1.数据库面向业务存储，仓库面向主题存储（主题：较高层次上对分析对象数据的一个完整并且一致的描述）
2.数据库针对应用（OLTP），仓库针对分析（OLAP）
3.数据库组织规范，仓库可能冗余，相对变化大，数据量大

2.3 检测与抓取

常用工具：
urllib、requests、scrapy
PhantomJS、beautifulSoup、Xpath

2.4 填写、埋点、日志

1.用户填写信息
2.APP或网页埋点（特点流程的信息记录点）
3.操作日志

2.5 计算

通过已有数据计算生成衍生数据

2.6 数据学习网站

数据竞赛网站（Kaggle&天池）
数据集网站（ImageNet/Open Images）
统计数据（统计局、政府机关、公司财报等）

三、单因子探索分析与可视化

3.1 理论铺垫

（1）集中趋势：均值、中位数与分位数、众数
四分位数计算方法：
Q1的位置= (n+1) × 0.25
Q2的位置= (n+1) × 0.5
Q3的位置= (n+1) × 0.75
实例1：
数据总量: 6, 47, 49, 15, 42, 41, 7, 39, 43, 40, 36
由小到大排列的结果: 6, 7, 15, 36, 39, 40, 41, 42, 43, 47, 49，一共11项
Q1 的位置=（11+1） × 0.25=3， Q2 的位置=（11+1）× 0.5=6， Q3的位置=（11+1） × 0.75=9，故
Q1 = 15，
Q2 = 40，
Q3 = 43
实例2：
数据总量: 7, 15, 36, 39, 40, 41，一共6项
数列项为偶数项时，四分位数Q2为该组数列的中数，
（n+1）/4= 7/4 =1.75，Q1在第一与第二个数字之间，
3（n+1）/4= 21/4 =5.25, Q3在第五与第六个数字之间，
Q1 = 0.7515+0.257 = 13，
Q2 = （36+39）/2= 37.5，
Q3 = 0.2541+0.7540 = 40.25.
（2）离中趋势：标准差、方差

注意：正太分布离中趋势，在-σ到σ概率未69%，在-1.96σ到1.96σ概率为95%，在-2.58σ到2.58σ概率为99%

（3）数据分布：偏态与峰态
偏态系数：数据平均值偏离状态的衡量
偏态系数 =0表示其数据分布形态与正态分布的偏斜程度相同；
偏态系数 >0表示其数据分布形态与正态分布相比为正偏（右偏），即有一条长尾巴拖在右边，数据右端有较多的极端值，数据均值右侧的离散程度强；均值相对较大。
偏态 <0表示其数据分布形态与正态分布相比为负偏（左偏），即有一条长尾拖在左边，数据左端有较多的极端值，数据均值左侧的离散程度强，均值相对较小。
举个例子，一组数，1 2 3 4 （6） 20，中位数是3，平均数是6。6比大多数数据都要大。偏态系数公式S如下：

峰态系数：数据分布集中强度的衡量,系数公式K如上。峰度又称峰态系数，表征概率密度分布曲线在平均值处峰值高低的特征数，即是描述总体中所有取值分布形态陡缓程度的统计量。直观看来，峰度反映了峰部的尖度。这个统计量需要与正态分布相比较。他的一个重要作用就是判断该分布是否是正态分布。
峰度 =0表示该总体数据分布与正态分布的陡缓程度相同；
峰度 >0表示该总体数据分布与正态分布相比较为陡峭，为尖顶峰；
峰度 <0表示该总体数据分布与正态分布相比较为平坦，为平顶峰。
峰度的绝对值数值越大表示其分布形态的陡缓程度与正态分布的差异程度越大。
（4）正态分布与三大分布

三大分布公式如下：

（5）抽样定理：抽样误差、抽样精度

δ²是总体方差，Zα 表示多少概率需要多少倍的σ，Δ²是我们要控制的方差，δ²是总体方差

下面看看实例1：

下面看看实例2：

原教程视频中计算有错误，我计算的是4条。

（6）编码实践上述理论

import pandas as pd
df = pd.read_csv('HR.csv')
df

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	sales	salary
0	0.38	0.53	2	157	3	0	1	0	sales	low
1	0.80	0.86	5	262	6	0	1	0	sales	medium
2	0.11	0.88	7	272	4	0	1	0	sales	medium
3	0.72	0.87	5	223	5	0	1	0	sales	low
4	0.37	0.52	2	159	3	0	1	0	sales	low
5	0.41	0.50	2	153	3	0	1	0	sales	low
6	0.10	0.77	6	247	4	0	1	0	sales	low
7	0.92	0.85	5	259	5	0	1	0	sales	low
8	0.89	1.00	5	224	5	0	1	0	sales	low
9	0.42	0.53	2	142	3	0	1	0	sales	low
10	0.45	0.54	2	135	3	0	1	0	sales	low
11	0.11	0.81	6	305	4	0	1	0	sales	low
12	0.84	0.92	4	234	5	0	1	0	sales	low
13	0.41	0.55	2	148	3	0	1	0	sales	low
14	0.36	0.56	2	137	3	0	1	0	sales	low
15	0.38	0.54	2	143	3	0	1	0	sales	low
16	0.45	0.47	2	160	3	0	1	0	sales	low
17	0.78	0.99	4	255	6	0	1	0	sales	low
18	0.45	0.51	2	160	3	1	1	1	sales	low
19	0.76	0.89	5	262	5	0	1	0	sales	low
20	0.11	0.83	6	282	4	0	1	0	sales	low
21	0.38	0.55	2	147	3	0	1	0	sales	low
22	0.09	0.95	6	304	4	0	1	0	sales	low
23	0.46	0.57	2	139	3	0	1	0	sales	low
24	0.40	0.53	2	158	3	0	1	0	sales	low
25	0.89	0.92	5	242	5	0	1	0	sales	low
26	0.82	0.87	4	239	5	0	1	0	sales	low
27	0.40	0.49	2	135	3	0	1	0	sales	low
28	0.41	0.46	2	128	3	0	1	0	accounting	low
29	0.38	0.50	2	132	3	0	1	0	accounting	low
...	...	...	...	...	...	...	...	...	...	...
14971	0.39	0.45	2	140	3	0	1	0	sales	medium
14972	0.11	0.97	6	310	4	0	1	0	accounting	medium
14973	0.36	0.52	2	143	3	0	1	0	accounting	medium
14974	0.36	0.54	2	153	3	0	1	0	accounting	medium
14975	0.10	0.79	7	310	4	0	1	0	hr	medium
14976	0.40	0.47	2	136	3	0	1	0	hr	medium
14977	0.81	0.85	4	251	6	0	1	0	hr	medium
14978	0.40	0.47	2	144	3	0	1	0	hr	medium
14979	0.09	0.93	6	296	4	0	1	0	technical	medium
14980	0.76	0.89	5	238	5	0	1	0	technical	high
14981	0.73	0.93	5	162	4	0	1	0	technical	low
14982	0.38	0.49	2	137	3	0	1	0	technical	medium
14983	0.72	0.84	5	257	5	0	1	0	technical	medium
14984	0.40	0.56	2	148	3	0	1	0	technical	medium
14985	0.91	0.99	5	254	5	0	1	0	technical	medium
14986	0.85	0.85	4	247	6	0	1	0	technical	low
14987	0.90	0.70	5	206	4	0	1	0	technical	low
14988	0.46	0.55	2	145	3	0	1	0	technical	low
14989	0.43	0.57	2	159	3	1	1	0	technical	low
14990	0.89	0.88	5	228	5	1	1	0	support	low
14991	0.09	0.81	6	257	4	0	1	0	support	low
14992	0.40	0.48	2	155	3	0	1	0	support	low
14993	0.76	0.83	6	293	6	0	1	0	support	low
14994	0.40	0.57	2	151	3	0	1	0	support	low
14995	0.37	0.48	2	160	3	0	1	0	support	low
14996	0.37	0.53	2	143	3	0	1	0	support	low
14997	0.11	0.96	6	280	4	0	1	0	support	low
14998	0.37	0.52	2	158	3	0	1	0	support	low
14999	NaN	0.52	2	223	5	0	1	0	support	low
15000	NaN	999999.00	2	159	3	0	1	0	support	nme

15001 rows × 10 columns

type(df)

pandas.core.frame.DataFrame

type(df["satisfaction_level"])

pandas.core.series.Series

df.mean()

satisfaction_level         0.612834
last_evaluation           67.378197
number_project             3.802813
average_montly_hours     201.048997
time_spend_company         3.498300
Work_accident              0.144590
left                       0.238184
promotion_last_5years      0.021265
dtype: float64

type(df.mean())

pandas.core.series.Series

df["satisfaction_level"].mean()

0.6128335222348166

df.median()

satisfaction_level         0.64
last_evaluation            0.72
number_project             4.00
average_montly_hours     200.00
time_spend_company         3.00
Work_accident              0.00
left                       0.00
promotion_last_5years      0.00
dtype: float64

df["satisfaction_level"].median()

0.64

df.quantile(q=0.25)

satisfaction_level         0.44
last_evaluation            0.56
number_project             3.00
average_montly_hours     156.00
time_spend_company         3.00
Work_accident              0.00
left                       0.00
promotion_last_5years      0.00
Name: 0.25, dtype: float64

df["satisfaction_level"].quantile(q=0.25)

0.44

df.mode()

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	sales	salary
0	0.1	0.55	4.0	135	3.0	0.0	0.0	0.0	sales	low
1	NaN	NaN	NaN	156	NaN	NaN	NaN	NaN	NaN	NaN

df["satisfaction_level"].mode()

0    0.1
dtype: float64

df["sales"].mode()

0    sales
dtype: object

df.std()

satisfaction_level          0.248631
last_evaluation          8164.679648
number_project              1.232686
average_montly_hours       49.941272
time_spend_company          1.460096
Work_accident               0.351699
left                        0.425987
promotion_last_5years       0.144272
dtype: float64

df["satisfaction_level"].std()

0.2486306510611418

df.var()

satisfaction_level       6.181720e-02
last_evaluation          6.666199e+07
number_project           1.519515e+00
average_montly_hours     2.494131e+03
time_spend_company       2.131880e+00
Work_accident            1.236922e-01
left                     1.814645e-01
promotion_last_5years    2.081443e-02
dtype: float64

df["satisfaction_level"].var()

0.061817200647087255

df.sum()

satisfaction_level                                                 9191.89
last_evaluation                                                1.01074e+06
number_project                                                       57046
average_montly_hours                                               3015936
time_spend_company                                                   52478
Work_accident                                                         2169
left                                                                  3573
promotion_last_5years                                                  319
sales                    salessalessalessalessalessalessalessalessaless...
salary                   lowmediummediumlowlowlowlowlowlowlowlowlowlowl...
dtype: object

df["satisfaction_level"].sum()

9191.89

df.skew()

satisfaction_level        -0.476360
last_evaluation          122.478569
number_project             0.337751
average_montly_hours       0.052887
time_spend_company         1.853157
Work_accident              2.021370
left                       1.229385
promotion_last_5years      6.637440
dtype: float64

df["satisfaction_level"].skew()  # 偏态系数

-0.4763603412839644

df.kurt()  # 峰态系数

satisfaction_level          -0.670859
last_evaluation          15000.999987
number_project              -0.495699
average_montly_hours        -1.134916
time_spend_company           4.772766
Work_accident                2.086216
left                        -0.488677
promotion_last_5years       42.061224
dtype: float64

df["satisfaction_level"].kurt()

-0.6708586220574557

import scipy.stats as ss

ss.norm   # 生成一个正态分布

ss.norm.stats(moments='mvsk')
# mvsk 
# m mean
# v  var
# s skew
# k kurt
# 下面输出的是标准正太分布的相关参数

(array(0.), array(1.), array(0.), array(0.))

ss.norm.pdf(0.0)  # 0.39894228....   pdf 是输入横坐标，输出纵坐标，分布函数在0处的值

0.3989422804014327

ss.norm.ppf(0.9)  # 输入参数必须0-1之间。
# 1.28155...   ppf 是一个累积值，从负无穷大到某点积分是0.9，这个点是多少。
# 负无穷到正无穷是1，当时0.9的时候，是多少

1.2815515655446004

ss.norm.cdf(2)  # 从负无穷到2,它的累积概率是多少

0.9772498680518208

ss.norm.cdf(2) - ss.norm.cdf(-2) # 0.95

0.9544997361036416

ss.norm.rvs(size=10)  # 得到10个符合正太分布的数字

array([-0.57057331, -0.7166785 ,  0.87394188,  0.24162614, -0.55360322,
        2.09826541,  0.40785991, -0.02672143, -0.73308176, -1.1403666 ])

ss.chi2  # 卡方分布，操作和正态分布一样。pdf,ppf等

ss.t  # t分布，操作和正态分布一样。pdf,ppf等

ss.f  # F分布，操作和正态分布一样。pdf,ppf等

df.sample(n=10)  # 抽样10个

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	sales	salary
12129	0.37	0.45	2	151	3	0	1	0	support	low
959	0.10	0.94	7	281	4	0	1	0	technical	medium
13851	0.51	0.52	3	188	3	0	0	0	technical	high
3398	0.64	0.50	3	238	4	0	0	0	technical	low
7820	0.12	0.84	4	218	6	0	0	0	technical	medium
9174	0.62	0.75	4	183	4	1	0	0	sales	low
14469	0.88	0.88	5	232	5	1	1	0	accounting	medium
2096	0.86	1.00	4	256	3	0	0	0	technical	medium
12619	0.43	0.51	2	141	3	0	1	0	sales	low
1406	0.15	0.62	4	257	3	0	1	0	hr	low

df.sample(frac=0.01)  # 按百分比抽样

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	sales	salary
13585	0.98	0.89	4	218	2	0	0	0	sales	medium
14226	0.38	0.54	2	143	3	0	1	0	sales	low
8034	0.90	0.53	3	270	3	0	0	0	sales	medium
2327	0.38	0.64	3	111	3	0	0	0	technical	medium
4455	0.68	1.00	6	258	5	0	0	0	sales	low
10915	0.98	0.67	4	209	6	0	0	0	marketing	low
14868	0.43	0.55	2	130	3	0	1	0	support	high
256	0.11	0.81	6	266	4	1	1	0	sales	medium
7548	0.96	0.78	3	209	2	0	0	0	product_mng	high
11487	0.75	0.53	4	224	4	1	0	0	support	medium
11448	0.57	0.46	3	186	3	1	0	0	IT	medium
7752	0.13	0.74	6	132	4	1	0	0	technical	medium
859	0.10	0.93	6	270	4	0	1	0	sales	low
2908	0.73	0.75	3	259	4	0	0	0	marketing	medium
8519	0.50	0.59	4	157	2	0	0	0	technical	low
6031	0.23	0.88	5	156	4	0	0	0	sales	low
13139	0.98	0.58	3	183	3	0	0	0	sales	low
5357	0.53	0.82	5	184	3	0	0	0	sales	medium
13446	0.65	0.62	4	258	2	0	0	0	support	high
13858	0.31	0.63	4	104	7	1	0	0	sales	medium
7008	0.56	0.68	3	109	3	0	0	0	IT	low
14682	0.44	0.53	2	149	3	0	1	0	sales	low
7519	0.18	0.86	6	264	3	0	0	0	technical	high
5014	0.92	1.00	3	212	2	0	0	0	support	low
2526	0.62	0.49	4	218	4	0	0	0	sales	medium
12563	0.10	0.77	7	291	4	0	1	0	accounting	low
11022	0.96	0.89	3	142	4	0	0	0	sales	medium
3440	0.96	0.61	3	140	3	0	0	0	marketing	low
11761	0.88	0.83	4	273	10	0	0	0	sales	medium
42	0.40	0.46	2	127	3	0	1	0	technical	low
...	...	...	...	...	...	...	...	...	...	...
3556	0.75	0.66	4	202	2	0	0	0	support	low
12170	0.81	0.99	4	259	5	0	1	0	sales	low
1724	0.92	0.89	4	241	5	0	1	0	technical	low
1867	0.44	0.48	2	158	3	0	1	0	technical	low
2117	0.78	0.72	5	270	3	1	0	0	technical	low
12660	0.44	0.50	2	130	3	0	1	0	support	medium
10126	0.93	0.71	4	272	2	0	0	0	support	medium
12949	0.68	0.84	3	270	3	0	0	0	support	high
14244	0.45	0.55	2	140	3	0	1	0	hr	low
14276	0.81	0.70	6	161	4	0	1	0	IT	medium
11376	0.95	0.52	3	183	2	1	0	0	sales	low
13005	0.66	0.80	4	192	3	0	0	0	hr	medium
709	0.42	0.48	2	140	3	0	1	0	sales	low
4094	0.30	0.80	6	250	3	0	0	0	support	low
4843	0.70	0.98	4	176	5	0	0	0	technical	low
268	0.38	0.56	2	156	3	0	1	0	technical	low
13334	0.99	0.86	3	167	2	0	0	0	sales	low
1154	0.39	0.53	2	131	3	0	1	0	sales	medium
5528	0.79	0.71	4	222	3	0	0	1	hr	high
2005	0.36	0.95	3	206	4	0	0	0	sales	low
2603	0.99	0.78	4	140	3	0	0	0	sales	medium
7789	0.77	0.78	2	271	3	0	0	0	management	low
11862	0.92	1.00	4	261	4	0	0	0	sales	medium
11388	0.52	0.80	3	252	4	0	0	0	product_mng	low
12168	0.32	0.50	2	135	5	0	1	0	sales	low
8909	0.68	0.85	3	250	3	0	0	0	support	low
12594	0.10	0.77	6	255	4	0	1	0	management	low
5498	0.97	1.00	5	251	2	0	0	0	accounting	medium
10947	0.94	0.73	3	196	3	0	0	0	hr	medium
2593	0.57	0.90	3	256	4	0	0	0	RandD	low

150 rows × 10 columns

df["satisfaction_level"].sample(10)

2512     0.22
3650     0.72
2121     0.75
8606     0.91
11965    0.84
13601    0.49
4951     0.50
12429    0.41
8820     0.23
2712     0.92
Name: satisfaction_level, dtype: float64

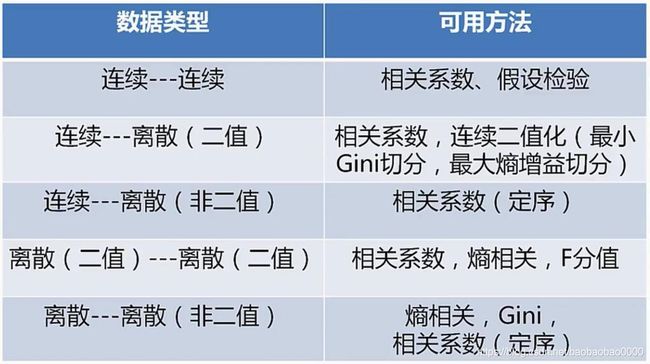
3.2 数据分类

定类（类别）：根据事物离散、无差别属性进行的分类，如：民族
定序（顺序）：可以界定数据的大小，但不能测定差值：如：收入的低、中、高
定距（间隔）：可以界定数据大小的同时，可测定差值，但无绝对零点（乘除法之类的无意义），如：温度
定比（比率）：可以界定数据大小，可测定差值，有绝对零点

3.3 单属性分析

（1）异常值分析

异常值有：离散异常值，连续异常值，知识异常值。

离散异常值：离散属性定义范围外的所有值均为异常值。比如空值；收入的中高低（如果出现其他结果就是异常值），可以标记出来单独处理。

知识异常值：在限定知识与常识范围外的所有值均为异常值。如身高10米的人。

连续异常值：通过四分位数确定。上界Q3 + k(Q3-Q1)> 正常值 >下界Q1 - k(Q3-Q1)，k取1.5-3。连续异常值可以舍弃或用边界值代替，具体业务具体分析。

（2）对比分析

通过比较的方式达到认识事实与了解数据的方法。
比什么：比较的对象是数，绝对数与相对数比较。绝对数就是绝对的数字，比如比较收入，比较身高等。相对数是把几个有联系的指标构成一个数，这个数就是相对数，相对数种类较多，常见的有：
结构相对数，创建的各种率，考试通过率，产品合格率等
比例相对数，总体内用不同部分的数值进行比较。比如传统三大产业的比例
比较相对数，同一时空下的相似或同质的指标进行对比，比如不同时期下同一商品的价格。
动态相对数：一般是有时间概念在里面，物理上的速度等
强度相对数：性质不同但有相互联系的属性进行联合，比如人均概念，我们GDP世界第二，人均就十几名了。
怎么比：
时间维度：同比是和去年同时期比较，环比就是和本年度上个月进行比较。
空间维度：现实方位空间（不同国家，城市等），逻辑空间（同公司不同部门）
经验与计划：经验比较，比如失业率达到多少就会社会大乱，我们需要警戒这个数据。
（3）结构分析
可以看成对比分析中比例相对数的分析，主要有两类，静态结构分析和动态结构分析。
静态结构分析就是直接分析总体的组成，比如我国三大产业的比例，即可了解我国产业结构。
动态结构分析就是以时间为轴，分析结构变化趋势。比如三大产业结构从一个五年计划到下一个五年计划占比变化。
（4）分布分析
1.直接获得概率分布：得到的数排列一下，得到一个分布。
2.判断是不是正态分布，如果是可以用正态分布结论分析该问题。可以通过偏态和峰态判断。
3.极大似然：顾名思义极大相似的样子，相似程度的衡量。给出一串数字，如果我们知道它属于正态分布，那一定可以确定一个均值一个方差。在该均值和方差确定的正态分布下，这串数字的这几个点在这个分布的取值也就是他们的概率，这些值的和或积是最大的，这个和或者积（要取对数）就叫做极大似然。确定是正态分布还是T分布或者F分布，那就比较他们在各自分布下的极大似然，哪个极大似然越大就更接近哪个分布。

3.4 单因子分析实战

这里我们对HR.csv进行分析实战

（1）satisfaction_level 的分析

import numpy as np
import pandas as pd

df = pd.read_csv("HR.csv")
df

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	sales	salary
0	0.38	0.53	2	157	3	0	1	0	sales	low
1	0.80	0.86	5	262	6	0	1	0	sales	medium
2	0.11	0.88	7	272	4	0	1	0	sales	medium
3	0.72	0.87	5	223	5	0	1	0	sales	low
4	0.37	0.52	2	159	3	0	1	0	sales	low
5	0.41	0.50	2	153	3	0	1	0	sales	low
6	0.10	0.77	6	247	4	0	1	0	sales	low
7	0.92	0.85	5	259	5	0	1	0	sales	low
8	0.89	1.00	5	224	5	0	1	0	sales	low
9	0.42	0.53	2	142	3	0	1	0	sales	low
10	0.45	0.54	2	135	3	0	1	0	sales	low
11	0.11	0.81	6	305	4	0	1	0	sales	low
12	0.84	0.92	4	234	5	0	1	0	sales	low
13	0.41	0.55	2	148	3	0	1	0	sales	low
14	0.36	0.56	2	137	3	0	1	0	sales	low
15	0.38	0.54	2	143	3	0	1	0	sales	low
16	0.45	0.47	2	160	3	0	1	0	sales	low
17	0.78	0.99	4	255	6	0	1	0	sales	low
18	0.45	0.51	2	160	3	1	1	1	sales	low
19	0.76	0.89	5	262	5	0	1	0	sales	low
20	0.11	0.83	6	282	4	0	1	0	sales	low
21	0.38	0.55	2	147	3	0	1	0	sales	low
22	0.09	0.95	6	304	4	0	1	0	sales	low
23	0.46	0.57	2	139	3	0	1	0	sales	low
24	0.40	0.53	2	158	3	0	1	0	sales	low
25	0.89	0.92	5	242	5	0	1	0	sales	low
26	0.82	0.87	4	239	5	0	1	0	sales	low
27	0.40	0.49	2	135	3	0	1	0	sales	low
28	0.41	0.46	2	128	3	0	1	0	accounting	low
29	0.38	0.50	2	132	3	0	1	0	accounting	low
...	...	...	...	...	...	...	...	...	...	...
14971	0.39	0.45	2	140	3	0	1	0	sales	medium
14972	0.11	0.97	6	310	4	0	1	0	accounting	medium
14973	0.36	0.52	2	143	3	0	1	0	accounting	medium
14974	0.36	0.54	2	153	3	0	1	0	accounting	medium
14975	0.10	0.79	7	310	4	0	1	0	hr	medium
14976	0.40	0.47	2	136	3	0	1	0	hr	medium
14977	0.81	0.85	4	251	6	0	1	0	hr	medium
14978	0.40	0.47	2	144	3	0	1	0	hr	medium
14979	0.09	0.93	6	296	4	0	1	0	technical	medium
14980	0.76	0.89	5	238	5	0	1	0	technical	high
14981	0.73	0.93	5	162	4	0	1	0	technical	low
14982	0.38	0.49	2	137	3	0	1	0	technical	medium
14983	0.72	0.84	5	257	5	0	1	0	technical	medium
14984	0.40	0.56	2	148	3	0	1	0	technical	medium
14985	0.91	0.99	5	254	5	0	1	0	technical	medium
14986	0.85	0.85	4	247	6	0	1	0	technical	low
14987	0.90	0.70	5	206	4	0	1	0	technical	low
14988	0.46	0.55	2	145	3	0	1	0	technical	low
14989	0.43	0.57	2	159	3	1	1	0	technical	low
14990	0.89	0.88	5	228	5	1	1	0	support	low
14991	0.09	0.81	6	257	4	0	1	0	support	low
14992	0.40	0.48	2	155	3	0	1	0	support	low
14993	0.76	0.83	6	293	6	0	1	0	support	low
14994	0.40	0.57	2	151	3	0	1	0	support	low
14995	0.37	0.48	2	160	3	0	1	0	support	low
14996	0.37	0.53	2	143	3	0	1	0	support	low
14997	0.11	0.96	6	280	4	0	1	0	support	low
14998	0.37	0.52	2	158	3	0	1	0	support	low
14999	NaN	0.52	2	223	5	0	1	0	support	low
15000	NaN	999999.00	2	159	3	0	1	0	support	nme

15001 rows × 10 columns

# 提取出列satisfaction_level数据
sl_s = df["satisfaction_level"]
sl_s

0        0.38
1        0.80
2        0.11
3        0.72
4        0.37
5        0.41
6        0.10
7        0.92
8        0.89
9        0.42
10       0.45
11       0.11
12       0.84
13       0.41
14       0.36
15       0.38
16       0.45
17       0.78
18       0.45
19       0.76
20       0.11
21       0.38
22       0.09
23       0.46
24       0.40
25       0.89
26       0.82
27       0.40
28       0.41
29       0.38
         ... 
14971    0.39
14972    0.11
14973    0.36
14974    0.36
14975    0.10
14976    0.40
14977    0.81
14978    0.40
14979    0.09
14980    0.76
14981    0.73
14982    0.38
14983    0.72
14984    0.40
14985    0.91
14986    0.85
14987    0.90
14988    0.46
14989    0.43
14990    0.89
14991    0.09
14992    0.40
14993    0.76
14994    0.40
14995    0.37
14996    0.37
14997    0.11
14998    0.37
14999     NaN
15000     NaN
Name: satisfaction_level, Length: 15001, dtype: float64

# 看看有没有异常值
sl_s[sl_s.isnull()]

14999   NaN
15000   NaN
Name: satisfaction_level, dtype: float64

# 看一下该行所有数据
df[df["satisfaction_level"].isnull()]

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	sales	salary
14999	NaN	0.52	2	223	5	0	1	0	support	low
15000	NaN	999999.00	2	159	3	0	1	0	support	nme

sl_s = sl_s.dropna()  # 丢弃异常值
sl_s

0        0.38
1        0.80
2        0.11
3        0.72
4        0.37
5        0.41
6        0.10
7        0.92
8        0.89
9        0.42
10       0.45
11       0.11
12       0.84
13       0.41
14       0.36
15       0.38
16       0.45
17       0.78
18       0.45
19       0.76
20       0.11
21       0.38
22       0.09
23       0.46
24       0.40
25       0.89
26       0.82
27       0.40
28       0.41
29       0.38
         ... 
14969    0.43
14970    0.78
14971    0.39
14972    0.11
14973    0.36
14974    0.36
14975    0.10
14976    0.40
14977    0.81
14978    0.40
14979    0.09
14980    0.76
14981    0.73
14982    0.38
14983    0.72
14984    0.40
14985    0.91
14986    0.85
14987    0.90
14988    0.46
14989    0.43
14990    0.89
14991    0.09
14992    0.40
14993    0.76
14994    0.40
14995    0.37
14996    0.37
14997    0.11
14998    0.37
Name: satisfaction_level, Length: 14999, dtype: float64

sl_s.mean()  # 均值

0.6128335222348166

sl_s.std()   # 标准差

0.2486306510611418

sl_s.quantile(q=0.25)  # 四分位数

0.44

sl_s.skew()  # 偏度

-0.4763603412839644

sl_s.kurt()  # 峰度

-0.6708586220574557

np.histogram(sl_s.values, bins=np.arange(0.0, 1.1, 0.1))
# 第一个参数为要切分的值，bins为分割点，输出结果表示
# 在0-0.1的数有195个，0.1-0.2有1214个以此类推

(array([ 195, 1214,  532,  974, 1668, 2146, 1972, 2074, 2220, 2004],
       dtype=int64),
 array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]))

（2）last_evaluation 的分析

le_s = df["last_evaluation"]
le_s

0             0.53
1             0.86
2             0.88
3             0.87
4             0.52
5             0.50
6             0.77
7             0.85
8             1.00
9             0.53
10            0.54
11            0.81
12            0.92
13            0.55
14            0.56
15            0.54
16            0.47
17            0.99
18            0.51
19            0.89
20            0.83
21            0.55
22            0.95
23            0.57
24            0.53
25            0.92
26            0.87
27            0.49
28            0.46
29            0.50
           ...    
14971         0.45
14972         0.97
14973         0.52
14974         0.54
14975         0.79
14976         0.47
14977         0.85
14978         0.47
14979         0.93
14980         0.89
14981         0.93
14982         0.49
14983         0.84
14984         0.56
14985         0.99
14986         0.85
14987         0.70
14988         0.55
14989         0.57
14990         0.88
14991         0.81
14992         0.48
14993         0.83
14994         0.57
14995         0.48
14996         0.53
14997         0.96
14998         0.52
14999         0.52
15000    999999.00
Name: last_evaluation, Length: 15001, dtype: float64

le_s[le_s.isnull()]

Series([], Name: last_evaluation, dtype: float64)

le_s.mean()

67.37819678688086

le_s.std()

8164.679647813715

le_s.median()

0.72

le_s.max()

999999.0

le_s.min()

0.36

le_s.skew()

122.47856947327085

le_s.kurt()

15000.999986811674

le_s[le_s>1]

15000    999999.0
Name: last_evaluation, dtype: float64

le_s = le_s[le_s < 1]
le_s

0        0.53
1        0.86
2        0.88
3        0.87
4        0.52
5        0.50
6        0.77
7        0.85
9        0.53
10       0.54
11       0.81
12       0.92
13       0.55
14       0.56
15       0.54
16       0.47
17       0.99
18       0.51
19       0.89
20       0.83
21       0.55
22       0.95
23       0.57
24       0.53
25       0.92
26       0.87
27       0.49
28       0.46
29       0.50
30       0.62
         ... 
14970    0.93
14971    0.45
14972    0.97
14973    0.52
14974    0.54
14975    0.79
14976    0.47
14977    0.85
14978    0.47
14979    0.93
14980    0.89
14981    0.93
14982    0.49
14983    0.84
14984    0.56
14985    0.99
14986    0.85
14987    0.70
14988    0.55
14989    0.57
14990    0.88
14991    0.81
14992    0.48
14993    0.83
14994    0.57
14995    0.48
14996    0.53
14997    0.96
14998    0.52
14999    0.52
Name: last_evaluation, Length: 14717, dtype: float64

q_low = le_s.quantile(q=0.25)
q_high = le_s.quantile(q=0.75)
q_interval = q_high - q_low
k = 1.5
le_s = le_s[le_s < q_high + k*q_interval][le_s > q_low - k*q_interval]
le_s

0        0.53
1        0.86
2        0.88
3        0.87
4        0.52
5        0.50
6        0.77
7        0.85
9        0.53
10       0.54
11       0.81
12       0.92
13       0.55
14       0.56
15       0.54
16       0.47
17       0.99
18       0.51
19       0.89
20       0.83
21       0.55
22       0.95
23       0.57
24       0.53
25       0.92
26       0.87
27       0.49
28       0.46
29       0.50
30       0.62
         ... 
14970    0.93
14971    0.45
14972    0.97
14973    0.52
14974    0.54
14975    0.79
14976    0.47
14977    0.85
14978    0.47
14979    0.93
14980    0.89
14981    0.93
14982    0.49
14983    0.84
14984    0.56
14985    0.99
14986    0.85
14987    0.70
14988    0.55
14989    0.57
14990    0.88
14991    0.81
14992    0.48
14993    0.83
14994    0.57
14995    0.48
14996    0.53
14997    0.96
14998    0.52
14999    0.52
Name: last_evaluation, Length: 14717, dtype: float64

np.histogram(le_s.values, bins=np.arange(0.0, 1.1, 0.1))

(array([   0,    0,    0,  179, 1389, 3396, 2234, 2062, 2752, 2705],
       dtype=int64),
 array([0. , 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1. ]))

le_s.mean()

0.7106292043215237

le_s.std()

0.1681755329761668

le_s.median()

0.71

le_s.max()

0.99

le_s.skew()

-0.02356916850081574

le_s.kurt()

-1.2395312667084741

（3）number_project 的分析

# 静态结构分析
np_s = df["number_project"]
np_s

0        2
1        5
2        7
3        5
4        2
5        2
6        6
7        5
8        5
9        2
10       2
11       6
12       4
13       2
14       2
15       2
16       2
17       4
18       2
19       5
20       6
21       2
22       6
23       2
24       2
25       5
26       4
27       2
28       2
29       2
        ..
14971    2
14972    6
14973    2
14974    2
14975    7
14976    2
14977    4
14978    2
14979    6
14980    5
14981    5
14982    2
14983    5
14984    2
14985    5
14986    4
14987    5
14988    2
14989    2
14990    5
14991    6
14992    2
14993    6
14994    2
14995    2
14996    2
14997    6
14998    2
14999    2
15000    2
Name: number_project, Length: 15001, dtype: int64

np_s[np_s.isnull()]

Series([], Name: number_project, dtype: int64)

np_s.mean()

3.8028131457902807

np_s.std()

1.232685990976685

np_s.median()

4.0

np_s.max()

7

np_s.min()

2

np_s.skew()

0.3377514421511209

np_s.kurt()

-0.4956991171815397

np_s.value_counts()

4    4365
3    4055
5    2761
2    2390
6    1174
7     256
Name: number_project, dtype: int64

np_s.value_counts(normalize=True)

4    0.290981
3    0.270315
5    0.184054
2    0.159323
6    0.078261
7    0.017066
Name: number_project, dtype: float64

np_s.value_counts(normalize=True).sort_index()

2    0.159323
3    0.270315
4    0.290981
5    0.184054
6    0.078261
7    0.017066
Name: number_project, dtype: float64

（4）average_montly_hours 的分析

amh = df["average_montly_hours"]
amh

0        157
1        262
2        272
3        223
4        159
5        153
6        247
7        259
8        224
9        142
10       135
11       305
12       234
13       148
14       137
15       143
16       160
17       255
18       160
19       262
20       282
21       147
22       304
23       139
24       158
25       242
26       239
27       135
28       128
29       132
        ... 
14971    140
14972    310
14973    143
14974    153
14975    310
14976    136
14977    251
14978    144
14979    296
14980    238
14981    162
14982    137
14983    257
14984    148
14985    254
14986    247
14987    206
14988    145
14989    159
14990    228
14991    257
14992    155
14993    293
14994    151
14995    160
14996    143
14997    280
14998    158
14999    223
15000    159
Name: average_montly_hours, Length: 15001, dtype: int64

amh.mean()

201.0489967335511

amh.std()

49.94127150123472

amh.max()

310

amh.min()

96

amh.skew()

0.05288710654474867

amh.kurt()

-1.1349155456035123

amh = amh[amh < amh.quantile(0.75) + 1.5*(amh.quantile(0.75) - amh.quantile(0.25))][amh > amh.quantile(0.25) - 1.5*(amh.quantile(0.75) - amh.quantile(0.25))]
amh

0        157
1        262
2        272
3        223
4        159
5        153
6        247
7        259
8        224
9        142
10       135
11       305
12       234
13       148
14       137
15       143
16       160
17       255
18       160
19       262
20       282
21       147
22       304
23       139
24       158
25       242
26       239
27       135
28       128
29       132
        ... 
14971    140
14972    310
14973    143
14974    153
14975    310
14976    136
14977    251
14978    144
14979    296
14980    238
14981    162
14982    137
14983    257
14984    148
14985    254
14986    247
14987    206
14988    145
14989    159
14990    228
14991    257
14992    155
14993    293
14994    151
14995    160
14996    143
14997    280
14998    158
14999    223
15000    159
Name: average_montly_hours, Length: 15001, dtype: int64

np.histogram(amh.values, bins=10)

(array([ 367, 1240, 2734, 1722, 1628, 1713, 1906, 2240, 1127,  324],
       dtype=int64),
 array([ 96. , 117.4, 138.8, 160.2, 181.6, 203. , 224.4, 245.8, 267.2,
        288.6, 310. ]))

np.histogram(amh.values, bins=np.arange(amh.min(), amh.max()+10, 10))
# bins左闭右开

(array([ 168,  171,  147,  807, 1153, 1234, 1073,  824,  818,  758,  751,
         738,  857,  824,  987, 1002, 1045,  935,  299,  193,  131,   86],
       dtype=int64),
 array([ 96, 106, 116, 126, 136, 146, 156, 166, 176, 186, 196, 206, 216,
        226, 236, 246, 256, 266, 276, 286, 296, 306, 316], dtype=int64))

amh.value_counts(bins=np.arange(amh.min(), amh.max()+10, 10))
# bins左开右闭

(146.0, 156.0]     1277
(136.0, 146.0]     1159
(256.0, 266.0]     1063
(236.0, 246.0]     1006
(156.0, 166.0]      993
(246.0, 256.0]      987
(126.0, 136.0]      886
(216.0, 226.0]      874
(266.0, 276.0]      860
(166.0, 176.0]      832
(226.0, 236.0]      814
(176.0, 186.0]      813
(186.0, 196.0]      761
(196.0, 206.0]      755
(206.0, 216.0]      731
(276.0, 286.0]      319
(95.999, 106.0]     187
(286.0, 296.0]      164
(116.0, 126.0]      162
(106.0, 116.0]      162
(296.0, 306.0]      128
(306.0, 316.0]       68
Name: average_montly_hours, dtype: int64

（5）time_spend_company 的分析

tsc_s = df["time_spend_company"]
tsc_s.value_counts()

3     6444
2     3244
4     2557
5     1474
6      718
10     214
7      188
8      162
Name: time_spend_company, dtype: int64

tsc_s.value_counts().sort_index()

2     3244
3     6444
4     2557
5     1474
6      718
7      188
8      162
10     214
Name: time_spend_company, dtype: int64

tsc_s.mean()

3.498300113325778

（6）Work_accident 的分析

wa_s = df["Work_accident"]
wa_s.value_counts()

0    12832
1     2169
Name: Work_accident, dtype: int64

wa_s.mean()

0.14459036064262382

（7）left 的分析

l_s = df["left"]
l_s.value_counts()

0    11428
1     3573
Name: left, dtype: int64

（8）promotion_last_5years 的分析

pl5_s = df["promotion_last_5years"]
pl5_s.value_counts()

0    14682
1      319
Name: promotion_last_5years, dtype: int64

（9）salary 的分析

s_s = df["salary"]
s_s.value_counts()

low       7317
medium    6446
high      1237
nme          1
Name: salary, dtype: int64

s_s.where(s_s == 'nme')

0        NaN
1        NaN
2        NaN
3        NaN
4        NaN
5        NaN
6        NaN
7        NaN
8        NaN
9        NaN
10       NaN
11       NaN
12       NaN
13       NaN
14       NaN
15       NaN
16       NaN
17       NaN
18       NaN
19       NaN
20       NaN
21       NaN
22       NaN
23       NaN
24       NaN
25       NaN
26       NaN
27       NaN
28       NaN
29       NaN
        ... 
14971    NaN
14972    NaN
14973    NaN
14974    NaN
14975    NaN
14976    NaN
14977    NaN
14978    NaN
14979    NaN
14980    NaN
14981    NaN
14982    NaN
14983    NaN
14984    NaN
14985    NaN
14986    NaN
14987    NaN
14988    NaN
14989    NaN
14990    NaN
14991    NaN
14992    NaN
14993    NaN
14994    NaN
14995    NaN
14996    NaN
14997    NaN
14998    NaN
14999    NaN
15000    nme
Name: salary, Length: 15001, dtype: object

s_s.where(s_s != 'nme')

0           low
1        medium
2        medium
3           low
4           low
5           low
6           low
7           low
8           low
9           low
10          low
11          low
12          low
13          low
14          low
15          low
16          low
17          low
18          low
19          low
20          low
21          low
22          low
23          low
24          low
25          low
26          low
27          low
28          low
29          low
          ...  
14971    medium
14972    medium
14973    medium
14974    medium
14975    medium
14976    medium
14977    medium
14978    medium
14979    medium
14980      high
14981       low
14982    medium
14983    medium
14984    medium
14985    medium
14986       low
14987       low
14988       low
14989       low
14990       low
14991       low
14992       low
14993       low
14994       low
14995       low
14996       low
14997       low
14998       low
14999       low
15000       NaN
Name: salary, Length: 15001, dtype: object

s_s.where(s_s != 'nme').dropna()

0           low
1        medium
2        medium
3           low
4           low
5           low
6           low
7           low
8           low
9           low
10          low
11          low
12          low
13          low
14          low
15          low
16          low
17          low
18          low
19          low
20          low
21          low
22          low
23          low
24          low
25          low
26          low
27          low
28          low
29          low
          ...  
14970    medium
14971    medium
14972    medium
14973    medium
14974    medium
14975    medium
14976    medium
14977    medium
14978    medium
14979    medium
14980      high
14981       low
14982    medium
14983    medium
14984    medium
14985    medium
14986       low
14987       low
14988       low
14989       low
14990       low
14991       low
14992       low
14993       low
14994       low
14995       low
14996       low
14997       low
14998       low
14999       low
Name: salary, Length: 15000, dtype: object

（9）sales 的分析

df.rename(columns={'sales': 'department'}, inplace=True)
d_s = df['department']
d_s.head()

0    sales
1    sales
2    sales
3    sales
4    sales
Name: department, dtype: object

d_s.value_counts(normalize=True)

sales          0.275982
technical      0.181321
support        0.148723
IT             0.081795
product_mng    0.060129
marketing      0.057196
RandD          0.052463
accounting     0.051130
hr             0.049263
management     0.041997
Name: department, dtype: float64

3.5 可视化

python可视化工具：matplotlib、seaborn、plotly

import seaborn as sns
import matplotlib.pyplot as plt

sns.set_style(style='whitegrid')  # 设置背景网格
sns.set_context(context='poster', font_scale=0.8)  # 图变为原图0.8倍
sns.set_palette(sns.color_palette("RdBu", n_colors=7))  # 设置图填充颜色
plt.title("ASLARY")   # 标题
plt.xlabel("salary")  # 横轴说明
plt.ylabel("Number")  # 纵轴说明
plt.xticks(np.arange(len(df['salary'].value_counts())), df["salary"].value_counts().index)
# 横轴标记

plt.axis([0, 4, 0, 10000])  # 界定横轴纵轴最大值最小值
# 给出横纵坐标画出图
plt.bar(np.arange(len(df['salary'].value_counts()))+0.5, df['salary'].value_counts(), width=0.5)
# 遍历标注数字
for x,y in zip(np.arange(len(df["salary"].value_counts()))+0.5, df["salary"].value_counts()):
    plt.text(x, y, y, ha="center", va="bottom")

# 运用seaborn画图
sns.countplot(x="salary", hue="department", data=df)

# 先把表格中的异常值处理了
df = df.dropna(axis=0, how='any')
df

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	department	salary
0	0.38	0.53	2	157	3	0	1	0	sales	low
1	0.80	0.86	5	262	6	0	1	0	sales	medium
2	0.11	0.88	7	272	4	0	1	0	sales	medium
3	0.72	0.87	5	223	5	0	1	0	sales	low
4	0.37	0.52	2	159	3	0	1	0	sales	low
5	0.41	0.50	2	153	3	0	1	0	sales	low
6	0.10	0.77	6	247	4	0	1	0	sales	low
7	0.92	0.85	5	259	5	0	1	0	sales	low
8	0.89	1.00	5	224	5	0	1	0	sales	low
9	0.42	0.53	2	142	3	0	1	0	sales	low
10	0.45	0.54	2	135	3	0	1	0	sales	low
11	0.11	0.81	6	305	4	0	1	0	sales	low
12	0.84	0.92	4	234	5	0	1	0	sales	low
13	0.41	0.55	2	148	3	0	1	0	sales	low
14	0.36	0.56	2	137	3	0	1	0	sales	low
15	0.38	0.54	2	143	3	0	1	0	sales	low
16	0.45	0.47	2	160	3	0	1	0	sales	low
17	0.78	0.99	4	255	6	0	1	0	sales	low
18	0.45	0.51	2	160	3	1	1	1	sales	low
19	0.76	0.89	5	262	5	0	1	0	sales	low
20	0.11	0.83	6	282	4	0	1	0	sales	low
21	0.38	0.55	2	147	3	0	1	0	sales	low
22	0.09	0.95	6	304	4	0	1	0	sales	low
23	0.46	0.57	2	139	3	0	1	0	sales	low
24	0.40	0.53	2	158	3	0	1	0	sales	low
25	0.89	0.92	5	242	5	0	1	0	sales	low
26	0.82	0.87	4	239	5	0	1	0	sales	low
27	0.40	0.49	2	135	3	0	1	0	sales	low
28	0.41	0.46	2	128	3	0	1	0	accounting	low
29	0.38	0.50	2	132	3	0	1	0	accounting	low
...	...	...	...	...	...	...	...	...	...	...
14969	0.43	0.46	2	157	3	0	1	0	sales	medium
14970	0.78	0.93	4	225	5	0	1	0	sales	medium
14971	0.39	0.45	2	140	3	0	1	0	sales	medium
14972	0.11	0.97	6	310	4	0	1	0	accounting	medium
14973	0.36	0.52	2	143	3	0	1	0	accounting	medium
14974	0.36	0.54	2	153	3	0	1	0	accounting	medium
14975	0.10	0.79	7	310	4	0	1	0	hr	medium
14976	0.40	0.47	2	136	3	0	1	0	hr	medium
14977	0.81	0.85	4	251	6	0	1	0	hr	medium
14978	0.40	0.47	2	144	3	0	1	0	hr	medium
14979	0.09	0.93	6	296	4	0	1	0	technical	medium
14980	0.76	0.89	5	238	5	0	1	0	technical	high
14981	0.73	0.93	5	162	4	0	1	0	technical	low
14982	0.38	0.49	2	137	3	0	1	0	technical	medium
14983	0.72	0.84	5	257	5	0	1	0	technical	medium
14984	0.40	0.56	2	148	3	0	1	0	technical	medium
14985	0.91	0.99	5	254	5	0	1	0	technical	medium
14986	0.85	0.85	4	247	6	0	1	0	technical	low
14987	0.90	0.70	5	206	4	0	1	0	technical	low
14988	0.46	0.55	2	145	3	0	1	0	technical	low
14989	0.43	0.57	2	159	3	1	1	0	technical	low
14990	0.89	0.88	5	228	5	1	1	0	support	low
14991	0.09	0.81	6	257	4	0	1	0	support	low
14992	0.40	0.48	2	155	3	0	1	0	support	low
14993	0.76	0.83	6	293	6	0	1	0	support	low
14994	0.40	0.57	2	151	3	0	1	0	support	low
14995	0.37	0.48	2	160	3	0	1	0	support	low
14996	0.37	0.53	2	143	3	0	1	0	support	low
14997	0.11	0.96	6	280	4	0	1	0	support	low
14998	0.37	0.52	2	158	3	0	1	0	support	low

14999 rows × 10 columns

df = df[df["last_evaluation"] <= 1][df["salary"] != 'nme']
df

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	department	salary
0	0.38	0.53	2	157	3	0	1	0	sales	low
1	0.80	0.86	5	262	6	0	1	0	sales	medium
2	0.11	0.88	7	272	4	0	1	0	sales	medium
3	0.72	0.87	5	223	5	0	1	0	sales	low
4	0.37	0.52	2	159	3	0	1	0	sales	low
5	0.41	0.50	2	153	3	0	1	0	sales	low
6	0.10	0.77	6	247	4	0	1	0	sales	low
7	0.92	0.85	5	259	5	0	1	0	sales	low
8	0.89	1.00	5	224	5	0	1	0	sales	low
9	0.42	0.53	2	142	3	0	1	0	sales	low
10	0.45	0.54	2	135	3	0	1	0	sales	low
11	0.11	0.81	6	305	4	0	1	0	sales	low
12	0.84	0.92	4	234	5	0	1	0	sales	low
13	0.41	0.55	2	148	3	0	1	0	sales	low
14	0.36	0.56	2	137	3	0	1	0	sales	low
15	0.38	0.54	2	143	3	0	1	0	sales	low
16	0.45	0.47	2	160	3	0	1	0	sales	low
17	0.78	0.99	4	255	6	0	1	0	sales	low
18	0.45	0.51	2	160	3	1	1	1	sales	low
19	0.76	0.89	5	262	5	0	1	0	sales	low
20	0.11	0.83	6	282	4	0	1	0	sales	low
21	0.38	0.55	2	147	3	0	1	0	sales	low
22	0.09	0.95	6	304	4	0	1	0	sales	low
23	0.46	0.57	2	139	3	0	1	0	sales	low
24	0.40	0.53	2	158	3	0	1	0	sales	low
25	0.89	0.92	5	242	5	0	1	0	sales	low
26	0.82	0.87	4	239	5	0	1	0	sales	low
27	0.40	0.49	2	135	3	0	1	0	sales	low
28	0.41	0.46	2	128	3	0	1	0	accounting	low
29	0.38	0.50	2	132	3	0	1	0	accounting	low
...	...	...	...	...	...	...	...	...	...	...
14969	0.43	0.46	2	157	3	0	1	0	sales	medium
14970	0.78	0.93	4	225	5	0	1	0	sales	medium
14971	0.39	0.45	2	140	3	0	1	0	sales	medium
14972	0.11	0.97	6	310	4	0	1	0	accounting	medium
14973	0.36	0.52	2	143	3	0	1	0	accounting	medium
14974	0.36	0.54	2	153	3	0	1	0	accounting	medium
14975	0.10	0.79	7	310	4	0	1	0	hr	medium
14976	0.40	0.47	2	136	3	0	1	0	hr	medium
14977	0.81	0.85	4	251	6	0	1	0	hr	medium
14978	0.40	0.47	2	144	3	0	1	0	hr	medium
14979	0.09	0.93	6	296	4	0	1	0	technical	medium
14980	0.76	0.89	5	238	5	0	1	0	technical	high
14981	0.73	0.93	5	162	4	0	1	0	technical	low
14982	0.38	0.49	2	137	3	0	1	0	technical	medium
14983	0.72	0.84	5	257	5	0	1	0	technical	medium
14984	0.40	0.56	2	148	3	0	1	0	technical	medium
14985	0.91	0.99	5	254	5	0	1	0	technical	medium
14986	0.85	0.85	4	247	6	0	1	0	technical	low
14987	0.90	0.70	5	206	4	0	1	0	technical	low
14988	0.46	0.55	2	145	3	0	1	0	technical	low
14989	0.43	0.57	2	159	3	1	1	0	technical	low
14990	0.89	0.88	5	228	5	1	1	0	support	low
14991	0.09	0.81	6	257	4	0	1	0	support	low
14992	0.40	0.48	2	155	3	0	1	0	support	low
14993	0.76	0.83	6	293	6	0	1	0	support	low
14994	0.40	0.57	2	151	3	0	1	0	support	low
14995	0.37	0.48	2	160	3	0	1	0	support	low
14996	0.37	0.53	2	143	3	0	1	0	support	low
14997	0.11	0.96	6	280	4	0	1	0	support	low
14998	0.37	0.52	2	158	3	0	1	0	support	low

14999 rows × 10 columns

（1）简单对比分析操作

# 以部门为单位对比
df.groupby("department").mean()

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years
department
IT	0.618142	0.716830	3.816626	202.215974	3.468623	0.133659	0.222494	0.002445
RandD	0.619822	0.712122	3.853875	200.800508	3.367217	0.170267	0.153748	0.034307
accounting	0.582151	0.717718	3.825293	201.162973	3.522816	0.125163	0.265971	0.018253
hr	0.598809	0.708850	3.654939	198.684709	3.355886	0.120433	0.290934	0.020298
management	0.621349	0.724000	3.860317	201.249206	4.303175	0.163492	0.144444	0.109524
marketing	0.618601	0.715886	3.687646	199.385781	3.569930	0.160839	0.236597	0.050117
product_mng	0.619634	0.714756	3.807095	199.965632	3.475610	0.146341	0.219512	0.000000
sales	0.614447	0.709717	3.776329	200.911353	3.534058	0.141787	0.244928	0.024155
support	0.618300	0.723109	3.803948	200.758188	3.393001	0.154778	0.248991	0.008973
technical	0.607897	0.721099	3.877941	202.497426	3.411397	0.140074	0.256250	0.010294

df.loc[:, ["last_evaluation", "department"]].groupby("department")

df.loc[:, ["last_evaluation", "department"]].groupby("department").mean()

	last_evaluation
department
IT	0.716830
RandD	0.712122
accounting	0.717718
hr	0.708850
management	0.724000
marketing	0.715886
product_mng	0.714756
sales	0.709717
support	0.723109
technical	0.721099

df.loc[:, ["average_montly_hours", "department"]].groupby("department")["average_montly_hours"].apply(lambda x: x.max()-x.min())

department
IT             212
RandD          210
accounting     213
hr             212
management     210
marketing      214
product_mng    212
sales          214
support        214
technical      213
Name: average_montly_hours, dtype: int64

（2）可视化—直方图

f = plt.figure()
f.add_subplot(1, 3, 1)
# ked分布图是否显示，hist直方图是否显示
sns.distplot(df["satisfaction_level"], bins=10)
f.add_subplot(1, 3, 2)
sns.distplot(df["last_evaluation"], bins=10)
f.add_subplot(1, 3, 3)
sns.distplot(df["average_montly_hours"], bins=10)

（3）可视化—箱线图

sns.boxplot(y=df["time_spend_company"])
# saturation分位数，whis是前面说的k

sns.boxplot(x=df["time_spend_company"], saturation=0.75, whis=3)
# saturation分位数，whis是前面说的k

（4）可视化—折线图

sub_df = df.groupby("time_spend_company").mean()
sns.pointplot(sub_df.index, sub_df["left"])
# 在公司呆的时间和离职率关系

sns.pointplot(x=“time_spend_company”, y=“left”, data=df)

（4）可视化—饼图

lbs = df["department"].value_counts().index  # 标签
# autopct添加数据
# colors指定颜色
plt.pie(df["department"].value_counts(normalize=True), labels=lbs, autopct="%1.1f%%", colors=sns.color_palette("Reds")) 
#seaborn没有饼图 

([,
  ,
  ,
  ,
  ,
  ,
  ,
  ,
  ,
  ],
 [Text(0.7117131257442415, 0.8387278620883902, 'sales'),
  Text(-0.7361690652250792, 0.8173463815333333, 'technical'),
  Text(-1.078295473144608, -0.21743705433031926, 'support'),
  Text(-0.6639038295740627, -0.8770585528212437, 'IT'),
  Text(-0.220711694218203, -1.0776299680480914, 'product_mng'),
  Text(0.1824348726672272, -1.0847661117655236, 'marketing'),
  Text(0.5381184913305728, -0.9593896441426228, 'RandD'),
  Text(0.8166516060190341, -0.7369397223562675, 'accounting'),
  Text(1.004980939261518, -0.4472284782088872, 'hr'),
  Text(1.090437030943069, -0.1447310662852455, 'management')],
 [Text(0.38820715949685897, 0.4574879247754855, '27.6%'),
  Text(-0.40154676285004315, 0.44582529901818174, '18.1%'),
  Text(-0.5881611671697861, -0.11860202963471958, '14.9%'),
  Text(-0.36212936158585235, -0.4783955742661329, '8.2%'),
  Text(-0.12038819684629253, -0.587798164389868, '6.0%'),
  Text(0.09950993054576027, -0.5916906064175583, '5.7%'),
  Text(0.2935191770894033, -0.5233034422596123, '5.2%'),
  Text(0.4454463305558367, -0.40196712128523676, '5.1%'),
  Text(0.5481714214153734, -0.24394280629575665, '4.9%'),
  Text(0.5947838350598559, -0.07894421797377027, '4.2%')])

# 凸显出sales部门
explodes = [0.1 if i=="sales" else 0 for i in lbs]
plt.pie(df["department"].value_counts(normalize=True), explode=explodes, labels=lbs, autopct="%1.1f%%", colors=sns.color_palette("Reds"))  

([,
  ,
  ,
  ,
  ,
  ,
  ,
  ,
  ,
  ],
 [Text(0.776414318993718, 0.9149758495509712, 'sales'),
  Text(-0.7361690652250792, 0.8173463815333333, 'technical'),
  Text(-1.078295473144608, -0.21743705433031926, 'support'),
  Text(-0.6639038295740627, -0.8770585528212437, 'IT'),
  Text(-0.220711694218203, -1.0776299680480914, 'product_mng'),
  Text(0.1824348726672272, -1.0847661117655236, 'marketing'),
  Text(0.5381184913305728, -0.9593896441426228, 'RandD'),
  Text(0.8166516060190341, -0.7369397223562675, 'accounting'),
  Text(1.004980939261518, -0.4472284782088872, 'hr'),
  Text(1.090437030943069, -0.1447310662852455, 'management')],
 [Text(0.45290835274633545, 0.5337359122380665, '27.6%'),
  Text(-0.40154676285004315, 0.44582529901818174, '18.1%'),
  Text(-0.5881611671697861, -0.11860202963471958, '14.9%'),
  Text(-0.36212936158585235, -0.4783955742661329, '8.2%'),
  Text(-0.12038819684629253, -0.587798164389868, '6.0%'),
  Text(0.09950993054576027, -0.5916906064175583, '5.7%'),
  Text(0.2935191770894033, -0.5233034422596123, '5.2%'),
  Text(0.4454463305558367, -0.40196712128523676, '5.1%'),
  Text(0.5481714214153734, -0.24394280629575665, '4.9%'),
  Text(0.5947838350598559, -0.07894421797377027, '4.2%')])

# salary分布
lbs = df["salary"].value_counts().index  # 标签
explodes = [0.1 if i=="low" else 0 for i in lbs]  # 强调low单独分隔出来
plt.pie(df["salary"].value_counts(normalize=True), explode=explodes, labels=lbs, autopct="%1.1f%%", colors=sns.color_palette("Reds")) 

([,
  ,
  ],
 [Text(0.04611030952732935, 1.1991137724816998, 'low'),
  Text(-0.32247422223497674, -1.051670279124568, 'medium'),
  Text(1.06328474507822, -0.28182539077227425, 'high')],
 [Text(0.026897680557608782, 0.6994830339476582, '48.8%'),
  Text(-0.1758950303099873, -0.5736383340679462, '43.0%'),
  Text(0.5799734973153926, -0.1537229404212405, '8.2%')])

小节

可视化还有很多图，散点图，雷达图等，可通过官网查阅学习。此外我们数据分析不应当只考虑某一个属性，而应该考虑多属性之间的联系，以及个体数据和总体数据联系。如某个员工满意度和他对公司评价两者之间有没有联系？某个人的工资和总体平均工资关系等。

四、多因子探索分析

上一章节我们介绍了探索性数据分析中的单因子分析和简单的对比分析概念与实践。我们一定要明白探索性数据分析最重要的作用是把数据的全貌进行展现，让数据分析者能根据数据进行决策。每个属性的数据除了自己本身所具有的性质外，属性与属性之间或者属性与某个已知成熟规律之间也可能会有联系。本章节就让我们着重分析属性与属性之间的常见联系的以及相关的分析方法。下面我们主要介绍这几个方面内容：假设检验与方差检验、相关系数与回归分析以及主成分分析和奇异值分解。

4.1 假设检验

假设检验就是根据一定的假设条件，从样本推断总体或者样本与样本之间的一种方法。换言之，假设检验就是提出一个假设，然后根据数据或者已知的分布性质来推断假设成立的概率有多大。具体步骤如下：

[

1.在假设检验中，我们常把假设和一个已知的分布关联起来，所以一般情况下，原假设的设定为符合该分布，而备择假设设定不符合该分布。

2.选择检验统计量，这个检验统计量是我们根据数据（如均值，方差等性质）构造的一个转换函数。构造这个函数的目的是让这个数据符合一个已知的分布，这样就可以利用相关的结论。比如，我们可以把一些数据减去它的均值再除以标准差。这样判断转换后的统计量也就是我们所说的检验统计量。其是否符合标准正态分布，即可以判断数据的分布是否是正态分布的概率了。

3.根据显著性水平确定拒绝域，显著性水平一般用希腊字母α表示，就是我们可以接受的失真程度的最大限度。显著性水平和相似度的相加和为1。比如我们确定了某数据属性有95%的可能性是某个分布，那么它的显著性水平就是5%。显著性水平一般是人为定的一个值，这个值定的越低那么就相当于对数据和分布的契合程度要求就越高。这个值我们一般取0.05也就是说要求数据有95%的可能与某分布一致。一旦确定了显著性水平，那么这个已知的分布上就可以画出一段与分布相似性较高的区域，我们叫做接受域。如果上一步说的检验统计量落入了拒绝域，那么H0就可以认为是假的，也就是可以被拒绝掉的。

4.计算p值或者样本统计值做出判断。根据计算的统计量和我们要比较的分布进行判断的过程。判断思路有两种，一个是区间估计的方法，计算一个检验统计量的分布区间，看这个区间是否包含了我们要比较的分布的特征。另一个方法就是计算一个p值，直接和显著性水平进行比较。p值可以理解成比我们计算出来的检验统计量结果更差的概率。如果p值小于α，那么这个假设就可以认为是假的。

下面我们来看一个例子：

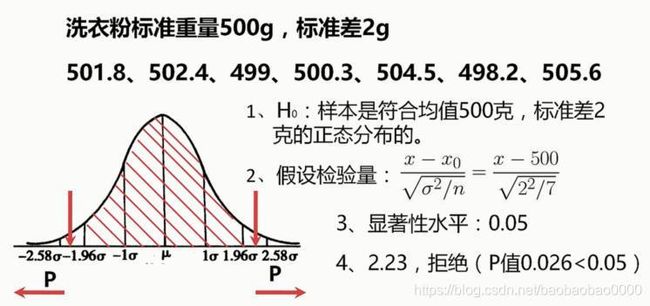
案例如上，一个洗衣粉制造厂，产出如下重量洗衣粉。历史经验告诉我们，洗衣粉标准质量为500g，标准差为2g。那么我们开始进行假设检验。

第一步，我们先确定原假设应尽可能接近于某分布，所以这里我们假设这些样本是符合均值500g标准差2g的正态分布。这就是原假设H0。备择假设就是不符合该正态分布。

第二步，我们就用上述假设构造它的统计量，如上图。它的分子是样本的均值减去我们假设的均值，它的分母则是每袋洗衣粉的误差。那么这个统计量应该是符合标准正态分布的。

第三步，确定显著性水平，我们选择0.05。一旦显著性水平确定了，就可以确定它的接受域，那么接受域以外就是它的拒绝域。拿正态分布图来说，±1.96倍标准差之间的范围，就是95%保证的范围，也就是我们所说的接受域。

第四步，计算检验统计量 计算p值。检验统计量我们可以得到2.23。2.23是通过将上面7组数据代入假设检验量的式子得到后的值的均值。因为得到了2.23.可以看出其已经超过了 0.05所在的1.96σ的范围，从2.23这个点到正无穷，其概率为 0.013，所有就是0.026，0.026小于0.05，它在拒绝域中，所以上面的假设是不能被接受的。计算步骤如下：

（501.8+502.4+499+500.3+504.5+498.2+505.6）/7 = 501.69
（501.69-500）/√（4/7） = 2.23

4.2 卡方检验

假设检验的方法有很多，这些方法的差别一般取决于检验统计量的选取上，比如上面我们使用的是μ检验法，还有卡方检验，p分布检验，F检验等流程上是一样的。知识检验时使用的统计量不同，应用的场景也可能有些差异。比如t分布检验常用来比较两组样本分布是否一致，像临床医疗上药物有没有效果就可以用t分布检验。F检验常用在方差分析，后面会介绍。

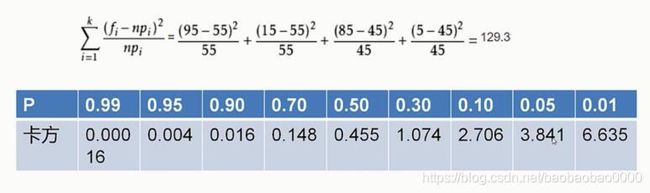
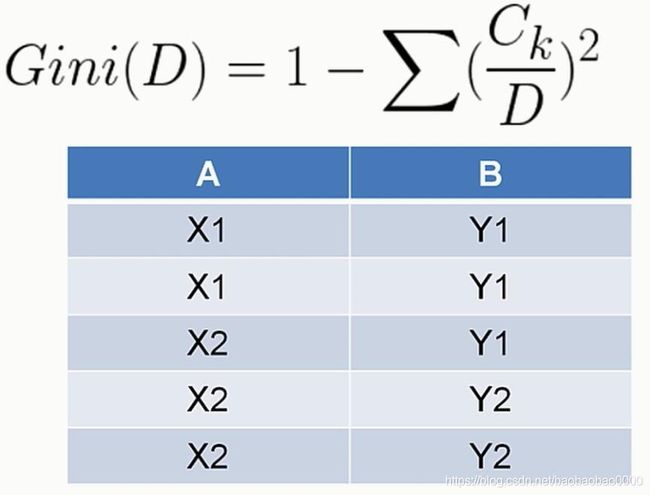
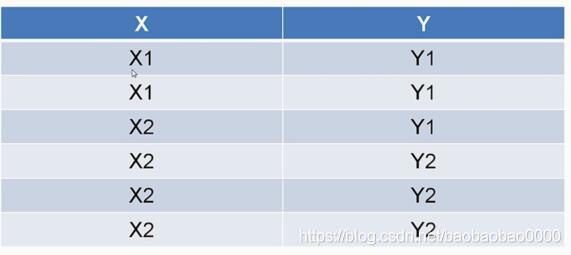
我们来看一下卡方检验的例子。如我们想看一下化妆这个行为和性别有没有关系。经过调查得到了这个图如下：

首先我们确定原假设，化妆与性别无关，以及所有的人群中化妆与不化妆的人群中男女分布都是一致的。然后假设检验量就是卡方分布的假设检验量，如上图中的公式，这个fi表示的是实际值，npi表示理论分布，如这张表中男士化妆，实际值是15，理论值是55。因为一共110人男女假设是一致的都是55，男士有100 女士也有100。我们把这些值都计算出来得到129.3，如下所示：

上图的的表示卡方值和p值的对应表，观察一下，发现如果p值取0.05的话，那么卡方值应该是不大于3.841。卡方值129.3明显大于3.841，所以我们可以拒绝原假设，得到的结论是性别与化妆与否是有比较强的关系的。即原假设性别与化妆与否没有关系，就可以被拒绝掉了。使用卡方检验进行这样的分析的方法，也叫做四格表检验法，常用来检验两个因素之间有没有比较强的联系。

4.3 方差检验

前面的例子中我们只研究了一个样本或者两个样本的研究方法。如果有多个样本，检验样本两两之间是不是有差异。一个思路就是用我们之前提到的方法进行两两分析。但这样对比次数可能就会比较大，如果数据样本数量比较多，就比较耗时耗力。还有一种方法就是我们要介绍的方差检验方法。因为它用到了F分布，所以也叫F检验。我们先来看个例子：

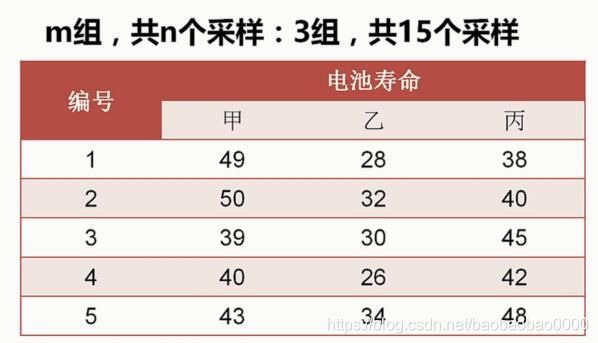
比如有三种电池，我们想看一下它们的寿命的均值是不是有差别。我们就可以使用方差检验方法。这里有两个参数大家需要重点关注一下，如图m，n。下面介绍三个公式。

1.第一个SST是用每个数据的数据值减去也就是刚才所说的那15个数据的均值，也就是每个数据减去均值它的平方和；

2.第二个SSM是指每一组的均值减去总体的均值的平方和；

3.最后一个SSE是每一个数减去它所属的组的平均值的平方和。

4.一般情况下带有SS指的都是平方和。SST就叫做总变差平方和；SSM叫做平均平方和，因为它指的是每个组与整体均值的平方和，所以也叫组间平方和；SSE就是残差平方和，因为它是指每个组内部的平方和，所以也叫组内平方和。

那么方差检验的检验统计量是什么呢？如下图：

知道了检验统计量，下面我们就可以开始我们的方差检验了。

第一步，我们还是确定它的原假设，也就是它们三个的均值是一定的，它们是没有差别的；

第二步，检验统计量我们也可以确定了是F值；

第三步，显著性水平还是设成0.05

第四步，计算
我们可以计算每个组的均值，分别是44.2，30和42.6，总体均值是38.93，然后求得SSM、SSE以及F的值，并且查表得到p的值如下：

p的值为0.00027小于0.05，所以可以拒绝原假设。即他们三者的均值是有差异的，而并不是没有差异的。

4.4 相关系数

1.相关系数是衡量两组数据或者说两组样本的分布趋势，变化趋势一致性程度的因子。相关系数有正相关负相关不相关之分。

2.相关系数越大越接近于1，二者变化趋势越正向同步。也就是说一个变大另一个也变大；一个变小另一个也跟着变小。

3.那么相关系数越小越接近于-1，二者的变化趋势越反向同步，也就是说一个数据变大，另外一个数据就会变小。

4.那么相关系数趋近于0，这二者可以认为是没有相关关系的。

常用的相关系数有两种：皮尔逊相关系数和斯皮尔曼相关系数。

（1）我们先来介绍一下皮尔逊相关系数，皮尔逊相关系数的形式如下：

皮尔逊相关系数它的分子是两组数的斜方差，而分母是两组数据的标准差的积。标准差的级相当于一个归一化因子。那么斜方差的定义展开就像右边的展开式一样。两组数据各减去它的均值，再进行相乘，取它的期望值。再看看上面两组小例子。

我们先计算第一个例子，E(X)=2/3,E(Y)=4/3,求出X-E(x)=(1/3, -2/3, 1/3),Y-E(Y)=(2/3, -4/3, 2/3)，再求出他们的期望为:

(1/3 * 2/3 + (-2/3) * (-4/3) + 1/3 * 2/3)/3 = 4/9，分子部分计算完毕

分母部分直接求出他们的方差再开方即可，结果也为4/9。故最后的结果r = 1。下面例子同理可求。

（2）我们再来介绍一下皮尔逊相关系数，皮尔逊相关系数的形式如下：

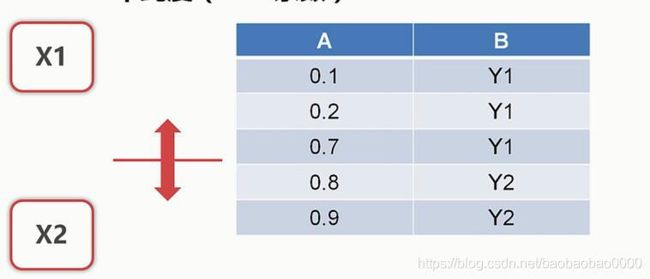
这里的n指的是每组数据的数量，这里的d指的是两组数据排名后的名次差。下面来看上述图片中的例子。

X值如上，X排名后，从小到大排列6排第一，11排第三，8排第二。同理Y也是如此。然后把排名后的名次做差值得到d。然后带入公式得到ρs = -0.5，那么斯皮尔曼相关系数就是负的0.5。

斯皮尔曼相关系数只跟它的名次差有关。它跟具体的数值关系不是那么大，这点和皮尔逊相关系数是不一样的。比如说我们把x的6换成一个更小的数，那么它的斯皮尔曼相关系数也不变，还是-0.5。同理Y也是如此。所以斯皮尔曼相关系数应用于相对比较的情况下比较适合。

4.5 线性回归

什么是回归？
回归是指确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
那么如果所谓的因变量与自变量的这种依赖关系是线性的关系，那么就是线性回归。线性回归最常见的解法就是最小二乘法。最小二乘法的本质就是最小化误差的平方的方法。公式如下：

这个方程相信大家都很熟悉，最小二乘法。那么通过这样的公式，求出它的因子b再求出它的结局a，就可以得到它的回归方程，这个公式高中大学都学过，具体原理可以网上查阅，这里不再赘述。具体可以参考链接：https://blog.csdn.net/weixin_38278993/article/details/100556051。

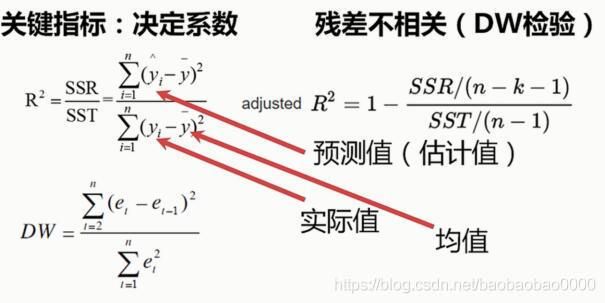
线性回归的效果的判定，主要有以下两种度量：一个是决定系数；另外一个是残差不相关。相关参数如下：

左边的决定系数R²代表一元线性回归的决定系数的定义。那么右边是多元决定系数的定义。这里也有SSR和SST的概念。

注意看y上面带个箭头代表是预测值也叫估计值，这里的yi直接指的就是实际值。你这里的y_8指的就是整体的均值。

那么通过这样的公式就可以得到我们所谓的决定系数。那么决定这个决定系数越接近于1，说明它的回归效果是越好；越接近于0，它的回归效果就越差。那么对于多元线性回归的情况来说，采用了一种叫做校正式的决定系数，就如上图右侧所示，这里的k指的就是参数的个数。

此外，还有一个检验指标就是DW检验，定义如上图。这里的e指的是它的残差，残差就是预测值与实际值的差。比如说有10个回归预测值，就可以得到10组残差，将这些残差值以自变量从小到大的顺序排序，然后代入这个公式得到DW的值。那么这个值的范围是从0~4的。值为2代表残差不相关；接近于4代表残差正相关；接近于零代表残差负相关。

那么好的回归它的残差应该是不相关的，也就是说它的DW值是接近于二的。

4.6 主成分分析

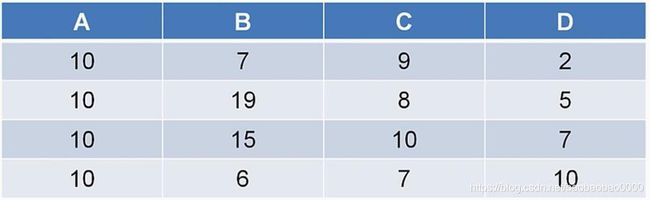
（1）我们在学习矩阵理论的时候，常把一个数据表看做一个空间，看做一个矩阵。那么这个矩阵的行对应每个数据对象的各个属性，矩阵的列就代表一个属性的不同内容。我们也常把每个属性当作由整个这张表构成空间的一个维度，每行所代表的实体代表的就是一个向量，这个表的内容代表的就是一个巨大的空间。下面来看个例子：

（2）这张表里有4个属性，每个属性都是一个维度。每一行的数据都包含4个维度，构成1个向量。虽然每1个向量有4个维度，但维度也是有主要次要之分的，比如维度A或者说是属性A。它就是一个比较次要的维度，因为通过它我们不能把几个对象区分开来，而维度b它的区分度就比较大，就可以认为是个明显的维度，是个主要的成分。更为灵活的可以通过正交变换将一组可能存在相关性的变量转化为一组线性不相关的变量。这一点相信学过线性代数的同学一定非常了解，在转化后的新的维度上，有的尺度被拉伸，有的尺度被收缩，我们取最能代表转化后维度的成分及尺度比较大的维度，就是主成分。

（3）那么相应的分析就是我们这里讲的主成分分析。那么这个变换过程就是PCA变换。PCA变换的一般过程为：

第一步求特征的斜方差矩阵；

第二步求斜方差矩阵的特征值和特征向量；

第三步将特征值按照从大到小的顺序排序，选择其中最大的k个；

第四步将样本点投影到选取的特征向量上

（4）下面让我们来看个例子

那么这张表里就有两个属性，而每条数据所对应的就有两个维度，那么它们构成的空间也就是一个我们所谓的二维空间，下面演示一下PCA变换的一般方法：
第一步求它的斜方差矩阵，即：
COV(X,X) COV(X,Y)
COV(Y,X) COV(Y,Y)
第二步，求它的特征值和特征向量，如上；
第三步，我们可以发现由于第二个特征值1.28，它远大于第一个特征值0.049，所以我们就可以用第二个特征值所代表的特征向量进行转换；
第四步，然后我们用它转换转换成了右边表的这么一个形式，注意这里矩阵相乘的形式是：x减去它的平均值，同时y再减去它的平均值，再和1.28对应特征向量进行相乘，最后得到最右边的矩阵。
这样就得到了它的主成分。再次提醒这不是两个矩阵直接相乘！！！

（5）主成分分析最重要的一个作用就是降维，有的时候我们会得到一个数据量，它的维度特别多，比如说它可能有几百个维度或者几千个维度，那么有些维度就是没有必要的，所以我们这个时候就需要把它最主要的成分提出来。通过主成分分析，我们已尽可能减少了失真，减少了比较大的工作量，使得后续的分析更加的快速简单。

（6）除了基本的PCA方法以外，奇异值分解也是一种常用的线性降维与成分提取的思路。那么奇异值分解也可以认为是一种PCA的方法。下面我们简单介绍一下：

奇异值分解它是将矩阵分解成如下形式：

中间是一个半正定矩阵，奇异值矩阵前后两个是两个酉阵，酉阵在实数域其实就是单位矩阵的意思。如果纠的更深的话，我们可以知道前面这个U代表在当前空间下的一组正交基，而后面V是指在进行变换后的空间下的一组正交基。通过奇异值矩阵的奇异值维度，比如取最大的一些奇异值，去掉一些较小的奇异值，同时缩小U和V的规模，就可以尽可能保留最主要的信息的情况下，减少数据的维度。

奇异值分解的方法涉及到矩阵理论的一些知识，涉及到的理论还是比较深的，比如说它是怎么推导的。这里我们就不多介绍了，感兴趣的可以翻开线性代数自行学习。我们这里先记住这个思路和方法，留着以后需要的时候用。

4.7 代码实现

import numpy as np
import scipy.stats as ss

norm_dist = ss.norm.rvs(size=20)  # 得到10个符合正态分布的数字
norm_dist

array([-0.33982896, -0.88293333,  1.13265041,  0.69182951, -1.61654312,
       -0.02629395,  0.84198628, -0.02742766,  0.7281102 , -0.66801634,
        1.14688624, -1.69580756, -1.67286388,  0.04195395, -0.24226755,
        0.86773833, -1.47738387, -3.11796742,  0.07911875,  0.03645439])

ss.normaltest(norm_dist) # p>0.05处于接受域，基于偏度与峰度检验。

NormaltestResult(statistic=2.6216280351175265, pvalue=0.2696005074915336)

# 检验前面男女化妆例子例子，卡方检验
ss.chi2_contingency([[15, 95], [85, 5]])
# 第一个为检验统计量，第二个为p值，第三个为自由度，最后是理论分布

(126.08080808080808, 2.9521414005078985e-29, 1, array([[55., 55.],
        [45., 45.]]))

# 独立t分布检验，检验两组值的均值有没有比较大的差异。遗忘的看看看前面内容
ss.ttest_ind(ss.norm.rvs(size=10), ss.norm.rvs(size=20))

Ttest_indResult(statistic=-1.8019008653997095, pvalue=0.08233819563557086)

# 放大值在看看结果。数据量越大，越能看出两个均值没差别
ss.ttest_ind(ss.norm.rvs(size=100), ss.norm.rvs(size=200))

Ttest_indResult(statistic=1.7615634824839101, pvalue=0.07916848366958461)

# 方差检验，继续参考前面例子
ss.f_oneway([49, 50, 39, 40, 43], [28, 32, 30, 26, 34], [38, 40, 45, 42, 48])

F_onewayResult(statistic=17.619417475728156, pvalue=0.0002687153079821641)

# qq图来对比一个分布是否符合一个已知分布。我们得到一个分布，
# 可以找到它的分位数，然后对应的分位数找到正态分布的分位数。横轴是正态分布的分位数的值，
# 纵轴是已知分布的值，这样就可以得到一个曲线。这个图如果正对xy轴角平分线，
# 与角平分线重合，那就是符合分布
from statsmodels.graphics.api import qqplot
from matplotlib import pyplot as plt

plt.show(qqplot(ss.norm.rvs(size=100)))  
# qq图默认检验一个分布是否是正态分布，所以输入一个分布也可
# 下图基本处于角平分线上

# 相关系数
import pandas as pd
s1 = pd.Series([0.1, 0.2, 1.1, 2.4, 1.3, 0.3, 0.5])
s2 = pd.Series([0.5, 0.4, 1.2, 2.5, 1.1, 0.7, 0.1])
s1.corr(s2)  '
# 求s1 s2相关系数

0.9333729600465923

s1.corr(s2, method="spearman")  # 指定斯皮尔曼相关系数

0.7142857142857144

df = pd.DataFrame([s1, s2])
print(df)
df.corr()  # 针对列进行计算的

     0    1    2    3    4    5    6
0  0.1  0.2  1.1  2.4  1.3  0.3  0.5
1  0.5  0.4  1.2  2.5  1.1  0.7  0.1

	0	1	2	3	4	5	6
0	1.0	1.0	1.0	1.0	-1.0	1.0	-1.0
1	1.0	1.0	1.0	1.0	-1.0	1.0	-1.0
2	1.0	1.0	1.0	1.0	-1.0	1.0	-1.0
3	1.0	1.0	1.0	1.0	-1.0	1.0	-1.0
4	-1.0	-1.0	-1.0	-1.0	1.0	-1.0	1.0
5	1.0	1.0	1.0	1.0	-1.0	1.0	-1.0
6	-1.0	-1.0	-1.0	-1.0	1.0	-1.0	1.0

df = pd.DataFrame(np.array([s1, s2]).T) # 转换成array再转置
df.corr()

	0	1
0	1.000000	0.933373
1	0.933373	1.000000

df.corr(method="spearman")  # 指定方法斯皮尔曼

	0	1
0	1.000000	0.714286
1	0.714286	1.000000

# 回归实例
x = np.arange(10).astype(np.float).reshape((10, 1))
y = x*3+4 + np.random.random((10, 1))
x

array([[0.],
       [1.],
       [2.],
       [3.],
       [4.],
       [5.],
       [6.],
       [7.],
       [8.],
       [9.]])

y

array([[ 4.29083244],
       [ 7.68188036],
       [10.0819889 ],
       [13.79384548],
       [16.69582671],
       [19.9952564 ],
       [22.96593519],
       [25.90420949],
       [28.65785762],
       [31.68954354]])

from sklearn.linear_model import LinearRegression

reg = LinearRegression()

res = reg.fit(x, y)  # 拟合

y_pred = reg.predict(x)
y_pred

array([[ 4.448071  ],
       [ 7.49865914],
       [10.54924727],
       [13.59983541],
       [16.65042354],
       [19.70101168],
       [22.75159982],
       [25.80218795],
       [28.85277609],
       [31.90336423]])

reg.coef_

array([[3.05058814]])

reg.intercept_

array([4.448071])

# PCA变换，还是前面那个例子，忘记的可以向前翻阅，就是data x   y那个表格例子
data = np.array([np.array([2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]),
                 np.array([2.4, 0.7, 2.9, 2.2, 3, 2.7, 1.6, 1.1, 1.6, 0.9])]).T

data

array([[2.5, 2.4],
       [0.5, 0.7],
       [2.2, 2.9],
       [1.9, 2.2],
       [3.1, 3. ],
       [2.3, 2.7],
       [2. , 1.6],
       [1. , 1.1],
       [1.5, 1.6],
       [1.1, 0.9]])

from sklearn.decomposition import PCA

'''
n_components: 
意义：PCA算法中所要保留的主成分个数n，也即保留下来的特征个数n
类型：int 或者 string，缺省时默认为None，所有成分被保留。
          赋值为int，比如n_components=1，将把原始数据降到一个维度。
          赋值为string，比如n_components='mle'，将自动选取特征个数n，使得满足所要求的方差百分比。
'''
lower_dim = PCA(n_components=1)  # 降维
lower_dim.fit(data)  # 修改data维度

PCA(copy=True, iterated_power='auto', n_components=1, random_state=None,
  svd_solver='auto', tol=0.0, whiten=False)

lower_dim.explained_variance_ratio_   # 维度的重要性，降维后得到了96%的信息量

array([0.96318131])

lower_dim.fit_transform(data)  # 得到转化后的数值

array([[-0.82797019],
       [ 1.77758033],
       [-0.99219749],
       [-0.27421042],
       [-1.67580142],
       [-0.9129491 ],
       [ 0.09910944],
       [ 1.14457216],
       [ 0.43804614],
       [ 1.22382056]])

注意：sklearn的PCA算法是基于奇异值矩阵的

# 下面开始动手写一个具体说明的PCA方法
from scipy import linalg
def myPCA(data, n_components = 10000000):
    mean_vals = np.mean(data, axis=0)  # 对列求均值
    mid = data - mean_vals
    cov_mat = np.cov(mid, rowvar=False)   # 求协方差矩阵
    eig_vals, eig_vects = linalg.eig(np.mat(cov_mat))  # 求出协方差矩阵的特征值特征向量
    eig_val_index = np.argsort(eig_vals)  # 按照升序（从小到大）进行快速排序，返回的是原数组的下标
    eig_val_index = eig_val_index[:-(n_components+1):-1]
    eig_vects = eig_vects[:, eig_val_index]
    low_dim_mat = np.dot(mid, eig_vects)
    return low_dim_mat, eig_vals
data = np.array([np.array([2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]),
                 np.array([2.4, 0.7, 2.9, 2.2, 3, 2.7, 1.6, 1.1, 1.6, 0.9])]).T

myPCA(data, n_components=1)  # 显示结果如下，和我们计算的结果基本一致

(array([[-0.82797019],
        [ 1.77758033],
        [-0.99219749],
        [-0.27421042],
        [-1.67580142],
        [-0.9129491 ],
        [ 0.09910944],
        [ 1.14457216],
        [ 0.43804614],
        [ 1.22382056]]), array([0.0490834 +0.j, 1.28402771+0.j]))

4.8 交叉分析方法与实现

接下来我们基于之前学习到的理论知识来进行属性间的数据分析。我们主要接触以下几种分析方法：

1.交叉分析

2.分组和钻取

3.相关分析

4.因子分析

5.回归分析

6.聚类分析

后面两个分析本章节不讲，后面细说。

（1）交叉分析

我们得到了一张数据表，需要进行分析的时候，最直观的我们有两个分析的切入点。一个是从列的角度进行分析，分析每个属性的特点并进行归纳和总结。另一个从行的角度进行分析，从case即案例的角度进行分析，尤其当数据有了标注的时候，以标注为关注点。案例分析越多，也就越接近于数据整体的质量。这两种分析方法也是最为浅层次的分析，如果仅仅进行这两方面的分析，有时并不能得到最为真实最为客观的结论。这是因为直接使用这种纵向分析和横向分析，忽略了数据间属性间的关联性，也就是说很可能有信息的失真。所以我们需要分析属性和属性之间的关系，得到更多的能反映数据内涵的信息。交叉分析就是一种重要的分析属性和属性之间关系的方法，交叉分析的含义比较广，所涉及到的分析方法也比较多。比如我们可以任意取两列，也就是两个属性，根据我们所学到的假设检验的方法来判断他们之间是否有联系。

也可以直接以一个或几个属性为行，令一个或几个属性为列做成一张交叉表也叫透视表。通过关注这张新生成的表的性质，可以更直观的分析两个属性或者几个属性之间的关系。

（2）下面我们进行代码演示

import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns

df = pd.read_csv("HR.csv")
df.tail()

	satisfaction_level	last_evaluation	number_project	average_montly_hours	time_spend_company	Work_accident	left	promotion_last_5years	department	salary
14994	0.40	0.57	2	151	3	0	1	0	support	low
14995	0.37	0.48	2	160	3	0	1	0	support	low
14996	0.37	0.53	2	143	3	0	1	0	support	low
14997	0.11	0.96	6	280	4	0	1	0	support	low
14998	0.37	0.52	2	158	3	0	1	0	support	low

# 得到各个部门离职率之间是否有差异，先得到各个部门的离职分布，
# 然后两两间求他们的t检验统计量并求出p值
dp_indices = df.groupby(by = "department").indices
dp_indices

{'IT': array([   61,    62,    63, ..., 14932, 14933, 14938], dtype=int64),
 'RandD': array([  301,   302,   303,   304,   305,   453,   454,   455,   456,
          457,   605,   606,   607,   608,   609,   833,   834,   835,
          836,   837,   985,   986,   987,   988,   989,  1061,  1062,
         1063,  1064,  1065,  1217,  1218,  1219,  1291,  1292,  1293,
         1294,  1295,  1296,  1368,  1369,  1370,  1371,  1372,  1373,
         1445,  1446,  1447,  1448,  1449,  1450,  1522,  1523,  1524,
         1525,  1526,  1598,  1599,  1600,  1601,  1602,  1675,  1676,
         1677,  1678,  1679,  1751,  1752,  1753,  1754,  1755,  1827,
         1828,  1829,  1830,  1831,  1903,  1904,  1905,  1906,  1907,
         1979,  1980,  1981,  1982,  1983,  2055,  2056,  2057,  2058,
         2059,  2131,  2132,  2133,  2134,  2135,  2207,  2208,  2209,
         2210,  2211,  2283,  2284,  2285,  2286,  2287,  2359,  2360,
         2361,  2362,  2363,  2435,  2436,  2437,  2438,  2439,  2511,
         2512,  2513,  2514,  2515,  2588,  2589,  2590,  2591,  2592,
         2593,  2665,  2666,  2667,  2668,  2669,  2670,  2742,  2743,
         2744,  2745,  2746,  2747,  2819,  2820,  2821,  2822,  2823,
         2824,  2896,  2897,  2898,  2899,  2900,  2972,  2973,  2974,
         2975,  2976,  3049,  3050,  3051,  3052,  3053,  3125,  3126,
         3127,  3128,  3129,  3201,  3202,  3203,  3204,  3205,  3277,
         3278,  3279,  3280,  3281,  3353,  3354,  3355,  3356,  3357,
         3429,  3430,  3431,  3432,  3433,  3505,  3506,  3507,  3508,
         3509,  3581,  3582,  3583,  3584,  3585,  3657,  3658,  3659,
         3660,  3661,  3733,  3734,  3735,  3736,  3737,  3809,  3810,
         3811,  3812,  3813,  3885,  3886,  3887,  3888,  3889,  3962,
         3963,  3964,  3965,  3966,  3967,  4039,  4040,  4041,  4042,
         4043,  4044,  4116,  4117,  4118,  4119,  4120,  4121,  4193,
         4194,  4195,  4196,  4197,  4198,  4270,  4271,  4272,  4273,
         4274,  4346,  4347,  4348,  4349,  4350,  4423,  4424,  4425,
         4426,  4427,  4499,  4500,  4501,  4502,  4503,  4575,  4576,
         4577,  4578,  4579,  4651,  4652,  4653,  4654,  4655,  4727,
         4728,  4729,  4730,  4731,  4803,  4804,  4805,  4806,  4807,
         4879,  4880,  4881,  4882,  4883,  4955,  4956,  4957,  4958,
         4959,  5031,  5032,  5033,  5034,  5035,  5107,  5108,  5109,
         5110,  5111,  5183,  5184,  5185,  5186,  5187,  5259,  5260,
         5261,  5262,  5263,  5336,  5337,  5338,  5339,  5340,  5341,
         5413,  5414,  5415,  5416,  5417,  5418,  5490,  5491,  5492,
         5493,  5494,  5495,  5567,  5568,  5569,  5570,  5571,  5572,
         5644,  5645,  5646,  5647,  5648,  5720,  5721,  5722,  5723,
         5724,  5797,  5798,  5799,  5800,  5801,  5873,  5874,  5875,
         5876,  5877,  5949,  5950,  5951,  5952,  5953,  6025,  6026,
         6027,  6028,  6029,  6101,  6102,  6103,  6104,  6105,  6177,
         6178,  6179,  6180,  6181,  6253,  6254,  6255,  6256,  6257,
         6329,  6330,  6331,  6332,  6333,  6405,  6406,  6407,  6408,
         6409,  6481,  6482,  6483,  6484,  6485,  6557,  6558,  6559,
         6560,  6561,  6633,  6634,  6635,  6636,  6637,  6710,  6711,
         6712,  6713,  6714,  6715,  6787,  6788,  6789,  6790,  6791,
         6792,  6864,  6865,  6866,  6867,  6868,  6869,  6941,  6942,
         6943,  6944,  6945,  6946,  7018,  7019,  7020,  7021,  7022,
         7094,  7095,  7096,  7097,  7098,  7171,  7172,  7173,  7174,
         7175,  7247,  7248,  7249,  7250,  7251,  7323,  7324,  7325,
         7326,  7327,  7399,  7400,  7401,  7402,  7403,  7475,  7476,
         7477,  7478,  7479,  7551,  7552,  7553,  7554,  7555,  7627,
         7628,  7629,  7630,  7631,  7703,  7704,  7705,  7706,  7707,
         7779,  7780,  7781,  7782,  7783,  7855,  7856,  7857,  7858,
         7859,  7931,  7932,  7933,  7934,  7935,  8007,  8008,  8009,
         8010,  8011,  8084,  8085,  8086,  8087,  8088,  8089,  8161,
         8162,  8163,  8164,  8165,  8166,  8238,  8239,  8240,  8241,
         8242,  8243,  8315,  8316,  8317,  8318,  8319,  8320,  8392,
         8393,  8394,  8395,  8396,  8468,  8469,  8470,  8471,  8472,
         8545,  8546,  8547,  8548,  8549,  8621,  8622,  8623,  8624,
         8625,  8697,  8698,  8699,  8700,  8701,  8773,  8774,  8775,
         8776,  8777,  8849,  8850,  8851,  8852,  8853,  8925,  8926,
         8927,  8928,  8929,  9001,  9002,  9003,  9004,  9005,  9077,
         9078,  9079,  9080,  9081,  9153,  9154,  9155,  9156,  9157,
         9229,  9230,  9231,  9232,  9233,  9305,  9306,  9307,  9308,
         9309,  9381,  9382,  9383,  9384,  9385,  9535,  9536,  9537,
         9538,  9539,  9540,  9689,  9690,  9691,  9692,  9693,  9694,
         9766,  9767,  9768,  9769,  9770, 10147, 10148, 10149, 10150,
        10151, 10223, 10224, 10225, 10226, 10227, 10299, 10300, 10301,
        10302, 10303, 10375, 10376, 10377, 10378, 10379, 10451, 10452,
        10453, 10454, 10455, 10527, 10528, 10529, 10530, 10531, 10603,
        10604, 10605, 10606, 10607, 10679, 10680, 10681, 10682, 10683,
        10755, 10756, 10757, 10758, 10759, 10832, 10833, 10834, 10835,
        10836, 10837, 10909, 10910, 10911, 10912, 10913, 10914, 10986,
        10987, 10988, 10989, 10990, 10991, 11001, 11002, 11003, 11004,
        11005, 11006, 11179, 11180, 11181, 11182, 11183, 11184, 11478,
        11479, 11480, 11481, 11482, 11483, 11659, 11660, 11661, 11662,
        11663, 11664, 12301, 12302, 12303, 12304, 12305, 12453, 12454,
        12455, 12456, 12457, 12605, 12606, 12607, 12608, 12609, 12814,
        12815, 12816, 12817, 12818, 12890, 12891, 12892, 12893, 12894,
        12966, 12967, 12968, 12969, 12970, 13043, 13044, 13045, 13046,
        13047, 13048, 13120, 13121, 13122, 13123, 13124, 13125, 13197,
        13198, 13199, 13200, 13201, 13202, 13212, 13213, 13214, 13215,
        13216, 13217, 13390, 13391, 13392, 13393, 13394, 13395, 13689,
        13690, 13691, 13692, 13693, 13694, 13870, 13871, 13872, 13873,
        13874, 13875, 14512, 14513, 14514, 14515, 14516, 14664, 14665,
        14666, 14667, 14668, 14816, 14817, 14818, 14819, 14820, 14939,
        14940, 14941, 14942, 14943], dtype=int64),
 'accounting': array([   28,    29,    30,    79,   105,   106,   107,   155,   181,
          182,   183,   224,   225,   232,   258,   259,   260,   308,
          334,   335,   336,   377,   378,   384,   410,   411,   412,
          460,   486,   487,   488,   529,   530,   536,   562,   563,
          564,   612,   638,   639,   640,   688,   714,   715,   716,
          764,   790,   791,   792,   840,   866,   867,   868,   916,
          942,   943,   944,   992,  1018,  1019,  1020,  1068,  1094,
         1095,  1096,  1145,  1171,  1172,  1173,  1222,  1248,  1249,
         1250,  1299,  1325,  1326,  1327,  1376,  1402,  1403,  1404,
         1453,  1479,  1480,  1481,  1529,  1555,  1556,  1557,  1606,
         1632,  1633,  1634,  1682,  1708,  1709,  1710,  1758,  1784,
         1785,  1786,  1834,  1860,  1861,  1862,  1910,  1936,  1937,
         1938,  1986,  2012,  2013,  2014,  2062,  2088,  2089,  2090,
         2138,  2164,  2165,  2166,  2214,  2240,  2241,  2242,  2290,
         2316,  2317,  2318,  2366,  2392,  2393,  2394,  2442,  2468,
         2469,  2470,  2519,  2545,  2546,  2547,  2596,  2622,  2623,
         2624,  2673,  2699,  2700,  2701,  2750,  2776,  2777,  2778,
         2827,  2853,  2854,  2855,  2903,  2929,  2930,  2931,  2980,
         3006,  3007,  3008,  3056,  3082,  3083,  3084,  3132,  3158,
         3159,  3160,  3208,  3234,  3235,  3236,  3284,  3310,  3311,
         3312,  3360,  3386,  3387,  3388,  3436,  3462,  3463,  3464,
         3512,  3538,  3539,  3540,  3588,  3614,  3615,  3616,  3664,
         3690,  3691,  3692,  3740,  3766,  3767,  3768,  3816,  3842,
         3843,  3844,  3893,  3919,  3920,  3921,  3970,  3996,  3997,
         3998,  4047,  4073,  4074,  4075,  4124,  4150,  4151,  4152,
         4201,  4227,  4228,  4229,  4277,  4303,  4304,  4305,  4354,
         4380,  4381,  4382,  4430,  4456,  4457,  4458,  4506,  4532,
         4533,  4534,  4582,  4608,  4609,  4610,  4658,  4684,  4685,
         4686,  4734,  4760,  4761,  4762,  4810,  4836,  4837,  4838,
         4886,  4912,  4913,  4914,  4962,  4988,  4989,  4990,  5038,
         5064,  5065,  5066,  5114,  5140,  5141,  5142,  5190,  5216,
         5217,  5218,  5267,  5293,  5294,  5295,  5344,  5370,  5371,
         5372,  5421,  5447,  5448,  5449,  5498,  5524,  5525,  5526,
         5575,  5601,  5602,  5603,  5651,  5677,  5678,  5679,  5728,
         5754,  5755,  5756,  5804,  5830,  5831,  5832,  5880,  5906,
         5907,  5908,  5956,  5982,  5983,  5984,  6032,  6058,  6059,
         6060,  6108,  6134,  6135,  6136,  6184,  6210,  6211,  6212,
         6260,  6286,  6287,  6288,  6336,  6362,  6363,  6364,  6412,
         6438,  6439,  6440,  6488,  6514,  6515,  6516,  6564,  6590,
         6591,  6592,  6641,  6667,  6668,  6669,  6718,  6744,  6745,
         6746,  6795,  6821,  6822,  6823,  6872,  6898,  6899,  6900,
         6949,  6975,  6976,  6977,  7025,  7051,  7052,  7053,  7102,
         7128,  7129,  7130,  7178,  7204,  7205,  7206,  7254,  7280,
         7281,  7282,  7330,  7356,  7357,  7358,  7406,  7432,  7433,
         7434,  7482,  7508,  7509,  7510,  7558,  7584,  7585,  7586,
         7634,  7660,  7661,  7662,  7710,  7736,  7737,  7738,  7786,
         7812,  7813,  7814,  7862,  7888,  7889,  7890,  7938,  7964,
         7965,  7966,  8015,  8041,  8042,  8043,  8092,  8118,  8119,
         8120,  8169,  8195,  8196,  8197,  8246,  8272,  8273,  8274,
         8323,  8349,  8350,  8351,  8399,  8425,  8426,  8427,  8476,
         8502,  8503,  8504,  8552,  8578,  8579,  8580,  8628,  8654,
         8655,  8656,  8704,  8730,  8731,  8732,  8780,  8806,  8807,
         8808,  8856,  8882,  8883,  8884,  8932,  8958,  8959,  8960,
         9008,  9034,  9035,  9036,  9084,  9110,  9111,  9112,  9160,
         9186,  9187,  9188,  9236,  9262,  9263,  9264,  9312,  9338,
         9339,  9340,  9389,  9415,  9416,  9417,  9466,  9492,  9493,
         9494,  9543,  9569,  9570,  9571,  9613,  9614,  9620,  9646,
         9647,  9648,  9697,  9723,  9724,  9725,  9773,  9799,  9800,
         9801,  9843,  9844,  9850,  9876,  9877,  9878,  9920,  9921,
         9926,  9952,  9953,  9954,  9996,  9997, 10002, 10028, 10029,
        10030, 10072, 10073, 10078, 10104, 10105, 10106, 10154, 10180,
        10181, 10182, 10230, 10256, 10257, 10258, 10306, 10332, 10333,
        10334, 10382, 10408, 10409, 10410, 10458, 10484, 10485, 10486,
        10534, 10560, 10561, 10562, 10610, 10636, 10637, 10638, 10686,
        10712, 10713, 10714, 10763, 10789, 10790, 10791, 10840, 10866,
        10867, 10868, 10917, 10943, 10944, 10945, 11009, 11035, 11036,
        11037, 11101, 11127, 11128, 11129, 11187, 11213, 11214, 11215,
        11277, 11303, 11304, 11305, 11400, 11429, 11457, 11486, 11581,
        11610, 11638, 11667, 11762, 11791, 11819, 11848, 11943, 11971,
        11972, 12028, 12029, 12030, 12079, 12105, 12106, 12107, 12155,
        12181, 12182, 12183, 12224, 12225, 12232, 12258, 12259, 12260,
        12308, 12334, 12335, 12336, 12377, 12378, 12384, 12410, 12411,
        12412, 12460, 12486, 12487, 12488, 12529, 12530, 12536, 12562,
        12563, 12564, 12612, 12638, 12639, 12640, 12688, 12714, 12715,
        12716, 12764, 12821, 12847, 12848, 12849, 12897, 12923, 12924,
        12925, 12974, 13000, 13001, 13002, 13051, 13077, 13078, 13079,
        13128, 13154, 13155, 13156, 13220, 13246, 13247, 13248, 13312,
        13338, 13339, 13340, 13398, 13424, 13425, 13426, 13488, 13514,
        13515, 13516, 13611, 13640, 13668, 13697, 13792, 13821, 13849,
        13878, 13973, 14002, 14030, 14059, 14154, 14182, 14183, 14239,
        14240, 14241, 14290, 14316, 14317, 14318, 14366, 14392, 14393,
        14394, 14435, 14436, 14443, 14469, 14470, 14471, 14519, 14545,
        14546, 14547, 14588, 14589, 14595, 14621, 14622, 14623, 14671,
        14697, 14698, 14699, 14740, 14741, 14747, 14773, 14774, 14775,
        14823, 14849, 14850, 14851, 14896, 14897, 14898, 14946, 14972,
        14973, 14974], dtype=int64),
 'hr': array([   31,    32,    33,    34,   108,   109,   110,   111,   184,
          185,   186,   187,   226,   227,   228,   261,   262,   263,
          264,   337,   338,   339,   340,   379,   380,   381,   413,
          414,   415,   416,   489,   490,   491,   492,   531,   532,
          533,   565,   566,   567,   568,   641,   642,   643,   644,
          717,   718,   719,   720,   793,   794,   795,   796,   869,
          870,   871,   872,   945,   946,   947,   948,  1021,  1022,
         1023,  1024,  1097,  1098,  1099,  1100,  1174,  1175,  1176,
         1177,  1251,  1252,  1253,  1254,  1328,  1329,  1330,  1331,
         1405,  1406,  1407,  1408,  1482,  1483,  1484,  1485,  1558,
         1559,  1560,  1561,  1635,  1636,  1637,  1638,  1711,  1712,
         1713,  1714,  1787,  1788,  1789,  1790,  1863,  1864,  1865,
         1866,  1939,  1940,  1941,  1942,  2015,  2016,  2017,  2018,
         2091,  2092,  2093,  2094,  2167,  2168,  2169,  2170,  2243,
         2244,  2245,  2246,  2319,  2320,  2321,  2322,  2395,  2396,
         2397,  2398,  2471,  2472,  2473,  2474,  2548,  2549,  2550,
         2551,  2625,  2626,  2627,  2628,  2702,  2703,  2704,  2705,
         2779,  2780,  2781,  2782,  2856,  2857,  2858,  2859,  2932,
         2933,  2934,  2935,  3009,  3010,  3011,  3012,  3085,  3086,
         3087,  3088,  3161,  3162,  3163,  3164,  3237,  3238,  3239,
         3240,  3313,  3314,  3315,  3316,  3389,  3390,  3391,  3392,
         3465,  3466,  3467,  3468,  3541,  3542,  3543,  3544,  3617,
         3618,  3619,  3620,  3693,  3694,  3695,  3696,  3769,  3770,
         3771,  3772,  3845,  3846,  3847,  3848,  3922,  3923,  3924,
         3925,  3999,  4000,  4001,  4002,  4076,  4077,  4078,  4079,
         4153,  4154,  4155,  4156,  4230,  4231,  4232,  4233,  4306,
         4307,  4308,  4309,  4383,  4384,  4385,  4386,  4459,  4460,
         4461,  4462,  4535,  4536,  4537,  4538,  4611,  4612,  4613,
         4614,  4687,  4688,  4689,  4690,  4763,  4764,  4765,  4766,
         4839,  4840,  4841,  4842,  4915,  4916,  4917,  4918,  4991,
         4992,  4993,  4994,  5067,  5068,  5069,  5070,  5143,  5144,
         5145,  5146,  5219,  5220,  5221,  5222,  5296,  5297,  5298,
         5299,  5373,  5374,  5375,  5376,  5450,  5451,  5452,  5453,
         5527,  5528,  5529,  5530,  5604,  5605,  5606,  5607,  5680,
         5681,  5682,  5683,  5757,  5758,  5759,  5760,  5833,  5834,
         5835,  5836,  5909,  5910,  5911,  5912,  5985,  5986,  5987,
         5988,  6061,  6062,  6063,  6064,  6137,  6138,  6139,  6140,
         6213,  6214,  6215,  6216,  6289,  6290,  6291,  6292,  6365,
         6366,  6367,  6368,  6441,  6442,  6443,  6444,  6517,  6518,
         6519,  6520,  6593,  6594,  6595,  6596,  6670,  6671,  6672,
         6673,  6747,  6748,  6749,  6750,  6824,  6825,  6826,  6827,
         6901,  6902,  6903,  6904,  6978,  6979,  6980,  6981,  7054,
         7055,  7056,  7057,  7131,  7132,  7133,  7134,  7207,  7208,
         7209,  7210,  7283,  7284,  7285,  7286,  7359,  7360,  7361,
         7362,  7435,  7436,  7437,  7438,  7511,  7512,  7513,  7514,
         7587,  7588,  7589,  7590,  7663,  7664,  7665,  7666,  7739,
         7740,  7741,  7742,  7815,  7816,  7817,  7818,  7891,  7892,
         7893,  7894,  7967,  7968,  7969,  7970,  8044,  8045,  8046,
         8047,  8121,  8122,  8123,  8124,  8198,  8199,  8200,  8201,
         8275,  8276,  8277,  8278,  8352,  8353,  8354,  8355,  8428,
         8429,  8430,  8431,  8505,  8506,  8507,  8508,  8581,  8582,
         8583,  8584,  8657,  8658,  8659,  8660,  8733,  8734,  8735,
         8736,  8809,  8810,  8811,  8812,  8885,  8886,  8887,  8888,
         8961,  8962,  8963,  8964,  9037,  9038,  9039,  9040,  9113,
         9114,  9115,  9116,  9189,  9190,  9191,  9192,  9265,  9266,
         9267,  9268,  9341,  9342,  9343,  9344,  9418,  9419,  9420,
         9421,  9495,  9496,  9497,  9498,  9572,  9573,  9574,  9575,
         9649,  9650,  9651,  9652,  9726,  9727,  9728,  9729,  9802,
         9803,  9804,  9805,  9879,  9880,  9881,  9882,  9955,  9956,
         9957,  9958, 10031, 10032, 10033, 10034, 10107, 10108, 10109,
        10110, 10183, 10184, 10185, 10186, 10259, 10260, 10261, 10262,
        10335, 10336, 10337, 10338, 10411, 10412, 10413, 10414, 10487,
        10488, 10489, 10490, 10563, 10564, 10565, 10566, 10639, 10640,
        10641, 10642, 10715, 10716, 10717, 10718, 10792, 10793, 10794,
        10795, 10869, 10870, 10871, 10872, 10946, 10947, 10948, 10949,
        11038, 11039, 11040, 11041, 11130, 11131, 11132, 11133, 11216,
        11217, 11218, 11219, 11306, 11307, 11308, 11309, 12031, 12032,
        12033, 12034, 12108, 12109, 12110, 12111, 12184, 12185, 12186,
        12187, 12226, 12227, 12228, 12261, 12262, 12263, 12264, 12337,
        12338, 12339, 12340, 12379, 12380, 12381, 12413, 12414, 12415,
        12416, 12489, 12490, 12491, 12492, 12531, 12532, 12533, 12565,
        12566, 12567, 12568, 12641, 12642, 12643, 12644, 12717, 12718,
        12719, 12720, 12850, 12851, 12852, 12853, 12926, 12927, 12928,
        12929, 13003, 13004, 13005, 13006, 13080, 13081, 13082, 13083,
        13157, 13158, 13159, 13160, 13249, 13250, 13251, 13252, 13341,
        13342, 13343, 13344, 13427, 13428, 13429, 13430, 13517, 13518,
        13519, 13520, 14242, 14243, 14244, 14245, 14319, 14320, 14321,
        14322, 14395, 14396, 14397, 14398, 14437, 14438, 14439, 14472,
        14473, 14474, 14475, 14548, 14549, 14550, 14551, 14590, 14591,
        14592, 14624, 14625, 14626, 14627, 14700, 14701, 14702, 14703,
        14742, 14743, 14744, 14776, 14777, 14778, 14779, 14852, 14853,
        14854, 14855, 14899, 14900, 14901, 14902, 14975, 14976, 14977,
        14978], dtype=int64),
 'management': array([   60,    82,   137,   158,   213,   235,   290,   311,   366,
          387,   442,   463,   518,   539,   594,   615,   670,   691,
          746,   767,   822,   843,   898,   919,   974,   995,  1050,
         1071,  1126,  1148,  1203,  1225,  1280,  1302,  1357,  1379,
         1434,  1456,  1511,  1532,  1587,  1609,  1664,  1685,  1740,
         1761,  1816,  1837,  1892,  1913,  1968,  1989,  2044,  2065,
         2120,  2141,  2196,  2217,  2272,  2293,  2348,  2369,  2424,
         2445,  2500,  2522,  2577,  2599,  2654,  2676,  2731,  2753,
         2808,  2830,  2885,  2906,  2961,  2983,  3038,  3059,  3114,
         3135,  3190,  3211,  3266,  3287,  3342,  3363,  3418,  3439,
         3494,  3515,  3570,  3591,  3646,  3667,  3722,  3743,  3798,
         3819,  3874,  3896,  3951,  3973,  4028,  4050,  4105,  4127,
         4182,  4204,  4259,  4280,  4335,  4357,  4412,  4433,  4488,
         4509,  4564,  4585,  4640,  4661,  4716,  4737,  4792,  4813,
         4868,  4889,  4944,  4965,  5020,  5041,  5096,  5117,  5172,
         5193,  5248,  5270,  5325,  5347,  5402,  5424,  5479,  5501,
         5556,  5578,  5633,  5654,  5709,  5731,  5786,  5807,  5862,
         5883,  5938,  5959,  6014,  6035,  6090,  6111,  6166,  6187,
         6242,  6263,  6318,  6339,  6394,  6415,  6470,  6491,  6546,
         6567,  6622,  6644,  6699,  6721,  6776,  6798,  6853,  6875,
         6930,  6952,  7007,  7028,  7083,  7105,  7160,  7181,  7236,
         7257,  7312,  7333,  7388,  7409,  7464,  7485,  7540,  7561,
         7616,  7637,  7692,  7713,  7768,  7789,  7844,  7865,  7920,
         7941,  7996,  8018,  8073,  8095,  8150,  8172,  8227,  8249,
         8304,  8326,  8381,  8402,  8457,  8479,  8534,  8555,  8610,
         8631,  8686,  8707,  8762,  8783,  8838,  8859,  8914,  8935,
         8990,  9011,  9066,  9087,  9142,  9163,  9218,  9239,  9294,
         9315,  9370,  9392,  9447,  9469,  9524,  9546,  9601,  9617,
         9623,  9678,  9700,  9755,  9776,  9831,  9847,  9853,  9908,
         9924,  9929,  9984, 10000, 10005, 10060, 10076, 10081, 10136,
        10157, 10212, 10233, 10288, 10309, 10364, 10385, 10440, 10461,
        10516, 10537, 10592, 10613, 10668, 10689, 10744, 10766, 10821,
        10843, 10898, 10920, 10975, 11012, 11067, 11078, 11079, 11080,
        11081, 11082, 11083, 11093, 11094, 11095, 11096, 11097, 11098,
        11104, 11159, 11190, 11245, 11256, 11257, 11258, 11259, 11260,
        11261, 11269, 11270, 11271, 11272, 11273, 11274, 11280, 11335,
        11346, 11347, 11348, 11349, 11350, 11351, 11392, 11393, 11394,
        11395, 11396, 11397, 11403, 11421, 11422, 11423, 11424, 11425,
        11426, 11432, 11449, 11450, 11451, 11452, 11453, 11454, 11460,
        11489, 11516, 11527, 11528, 11529, 11530, 11531, 11532, 11573,
        11574, 11575, 11576, 11577, 11578, 11584, 11602, 11603, 11604,
        11605, 11606, 11607, 11613, 11630, 11631, 11632, 11633, 11634,
        11635, 11641, 11670, 11697, 11708, 11709, 11710, 11711, 11712,
        11713, 11754, 11755, 11756, 11757, 11758, 11759, 11765, 11783,
        11784, 11785, 11786, 11787, 11788, 11794, 11811, 11812, 11813,
        11814, 11815, 11816, 11822, 11840, 11841, 11842, 11843, 11844,
        11845, 11851, 11878, 11889, 11890, 11891, 11892, 11893, 11894,
        11935, 11936, 11937, 11938, 11939, 11940, 11946, 11975, 11993,
        11994, 11995, 11996, 11997, 12060, 12082, 12137, 12158, 12213,
        12235, 12290, 12311, 12366, 12387, 12442, 12463, 12518, 12539,
        12594, 12615, 12670, 12691, 12746, 12767, 12803, 12824, 12879,
        12900, 12955, 12977, 13032, 13054, 13109, 13131, 13186, 13223,
        13278, 13289, 13290, 13291, 13292, 13293, 13294, 13304, 13305,
        13306, 13307, 13308, 13309, 13315, 13370, 13401, 13456, 13467,
        13468, 13469, 13470, 13471, 13472, 13480, 13481, 13482, 13483,
        13484, 13485, 13491, 13546, 13557, 13558, 13559, 13560, 13561,
        13562, 13603, 13604, 13605, 13606, 13607, 13608, 13614, 13632,
        13633, 13634, 13635, 13636, 13637, 13643, 13660, 13661, 13662,
        13663, 13664, 13665, 13671, 13700, 13727, 13738, 13739, 13740,
        13741, 13742, 13743, 13784, 13785, 13786, 13787, 13788, 13789,
        13795, 13813, 13814, 13815, 13816, 13817, 13818, 13824, 13841,
        13842, 13843, 13844, 13845, 13846, 13852, 13881, 13908, 13919,
        13920, 13921, 13922, 13923, 13924, 13965, 13966, 13967, 13968,
        13969, 13970, 13976, 13994, 13995, 13996, 13997, 13998, 13999,
        14005, 14022, 14023, 14024, 14025, 14026, 14027, 14033, 14051,
        14052, 14053, 14054, 14055, 14056, 14062, 14089, 14100, 14101,
        14102, 14103, 14104, 14105, 14146, 14147, 14148, 14149, 14150,
        14151, 14157, 14186, 14204, 14205, 14206, 14207, 14208, 14271,
        14293, 14348, 14369, 14424, 14446, 14501, 14522, 14577, 14598,
        14653, 14674, 14729, 14750, 14805, 14826, 14873, 14928, 14949],
       dtype=int64),
 'marketing': array([   77,    83,    84,    85,   148,   149,   150,   151,   152,
          153,   159,   160,   161,   229,   230,   236,   237,   238,
          306,   312,   313,   314,   382,   388,   389,   390,   458,
          464,   465,   466,   534,   540,   541,   542,   610,   616,
          617,   618,   686,   692,   693,   694,   762,   768,   769,
          770,   838,   844,   845,   846,   914,   920,   921,   922,
          990,   996,   997,   998,  1066,  1072,  1073,  1074,  1142,
         1143,  1149,  1150,  1151,  1220,  1226,  1227,  1228,  1297,
         1303,  1304,  1305,  1374,  1380,  1381,  1382,  1451,  1457,
         1458,  1459,  1527,  1533,  1534,  1535,  1603,  1604,  1610,
         1611,  1612,  1680,  1686,  1687,  1688,  1756,  1762,  1763,
         1764,  1832,  1838,  1839,  1840,  1908,  1914,  1915,  1916,
         1984,  1990,  1991,  1992,  2060,  2066,  2067,  2068,  2136,
         2142,  2143,  2144,  2212,  2218,  2219,  2220,  2288,  2294,
         2295,  2296,  2364,  2370,  2371,  2372,  2440,  2446,  2447,
         2448,  2516,  2517,  2523,  2524,  2525,  2594,  2600,  2601,
         2602,  2671,  2677,  2678,  2679,  2748,  2754,  2755,  2756,
         2825,  2831,  2832,  2833,  2901,  2907,  2908,  2909,  2977,
         2978,  2984,  2985,  2986,  3054,  3060,  3061,  3062,  3130,
         3136,  3137,  3138,  3206,  3212,  3213,  3214,  3282,  3288,
         3289,  3290,  3358,  3364,  3365,  3366,  3434,  3440,  3441,
         3442,  3510,  3516,  3517,  3518,  3586,  3592,  3593,  3594,
         3662,  3668,  3669,  3670,  3738,  3744,  3745,  3746,  3814,
         3820,  3821,  3822,  3890,  3891,  3897,  3898,  3899,  3968,
         3974,  3975,  3976,  4045,  4051,  4052,  4053,  4122,  4128,
         4129,  4130,  4199,  4205,  4206,  4207,  4275,  4281,  4282,
         4283,  4351,  4352,  4358,  4359,  4360,  4428,  4434,  4435,
         4436,  4504,  4510,  4511,  4512,  4580,  4586,  4587,  4588,
         4656,  4662,  4663,  4664,  4732,  4738,  4739,  4740,  4808,
         4814,  4815,  4816,  4884,  4890,  4891,  4892,  4960,  4966,
         4967,  4968,  5036,  5042,  5043,  5044,  5112,  5118,  5119,
         5120,  5188,  5194,  5195,  5196,  5264,  5265,  5271,  5272,
         5273,  5342,  5348,  5349,  5350,  5419,  5425,  5426,  5427,
         5496,  5502,  5503,  5504,  5573,  5579,  5580,  5581,  5649,
         5655,  5656,  5657,  5725,  5726,  5732,  5733,  5734,  5802,
         5808,  5809,  5810,  5878,  5884,  5885,  5886,  5954,  5960,
         5961,  5962,  6030,  6036,  6037,  6038,  6106,  6112,  6113,
         6114,  6182,  6188,  6189,  6190,  6258,  6264,  6265,  6266,
         6334,  6340,  6341,  6342,  6410,  6416,  6417,  6418,  6486,
         6492,  6493,  6494,  6562,  6568,  6569,  6570,  6638,  6639,
         6645,  6646,  6647,  6716,  6722,  6723,  6724,  6793,  6799,
         6800,  6801,  6870,  6876,  6877,  6878,  6947,  6953,  6954,
         6955,  7023,  7029,  7030,  7031,  7099,  7100,  7106,  7107,
         7108,  7176,  7182,  7183,  7184,  7252,  7258,  7259,  7260,
         7328,  7334,  7335,  7336,  7404,  7410,  7411,  7412,  7480,
         7486,  7487,  7488,  7556,  7562,  7563,  7564,  7632,  7638,
         7639,  7640,  7708,  7714,  7715,  7716,  7784,  7790,  7791,
         7792,  7860,  7866,  7867,  7868,  7936,  7942,  7943,  7944,
         8012,  8013,  8019,  8020,  8021,  8090,  8096,  8097,  8098,
         8167,  8173,  8174,  8175,  8244,  8250,  8251,  8252,  8321,
         8327,  8328,  8329,  8397,  8403,  8404,  8405,  8473,  8474,
         8480,  8481,  8482,  8550,  8556,  8557,  8558,  8626,  8632,
         8633,  8634,  8702,  8708,  8709,  8710,  8778,  8784,  8785,
         8786,  8854,  8860,  8861,  8862,  8930,  8936,  8937,  8938,
         9006,  9012,  9013,  9014,  9082,  9088,  9089,  9090,  9158,
         9164,  9165,  9166,  9234,  9240,  9241,  9242,  9310,  9316,
         9317,  9318,  9386,  9387,  9393,  9394,  9395,  9458,  9459,
         9460,  9461,  9462,  9463,  9464,  9470,  9471,  9472,  9541,
         9547,  9548,  9549,  9612,  9618,  9624,  9625,  9626,  9695,
         9701,  9702,  9703,  9771,  9777,  9778,  9779,  9842,  9848,
         9854,  9855,  9856,  9919,  9930,  9931,  9932,  9995, 10006,
        10007, 10008, 10071, 10082, 10083, 10084, 10152, 10158, 10159,
        10160, 10228, 10234, 10235, 10236, 10304, 10310, 10311, 10312,
        10380, 10386, 10387, 10388, 10456, 10462, 10463, 10464, 10532,
        10538, 10539, 10540, 10608, 10614, 10615, 10616, 10684, 10690,
        10691, 10692, 10760, 10761, 10767, 10768, 10769, 10838, 10844,
        10845, 10846, 10915, 10921, 10922, 10923, 11007, 11013, 11014,
        11015, 11099, 11105, 11106, 11107, 11185, 11191, 11192, 11193,
        11275, 11281, 11282, 11283, 11398, 11404, 11405, 11406, 11427,
        11433, 11434, 11435, 11455, 11461, 11462, 11463, 11484, 11490,
        11491, 11492, 11579, 11585, 11586, 11587, 11608, 11614, 11615,
        11616, 11636, 11642, 11643, 11644, 11665, 11671, 11672, 11673,
        11760, 11766, 11767, 11768, 11789, 11795, 11796, 11797, 11817,
        11823, 11824, 11825, 11846, 11852, 11853, 11854, 11941, 11947,
        11948, 11949, 11970, 11976, 11977, 11978, 11998, 12077, 12083,
        12084, 12085, 12148, 12149, 12150, 12151, 12152, 12153, 12159,
        12160, 12161, 12229, 12230, 12236, 12237, 12238, 12306, 12312,
        12313, 12314, 12382, 12388, 12389, 12390, 12458, 12464, 12465,
        12466, 12534, 12540, 12541, 12542, 12610, 12616, 12617, 12618,
        12686, 12692, 12693, 12694, 12762, 12768, 12769, 12770, 12819,
        12825, 12826, 12827, 12895, 12901, 12902, 12903, 12971, 12972,
        12978, 12979, 12980, 13049, 13055, 13056, 13057, 13126, 13132,
        13133, 13134, 13218, 13224, 13225, 13226, 13310, 13316, 13317,
        13318, 13396, 13402, 13403, 13404, 13486, 13492, 13493, 13494,
        13609, 13615, 13616, 13617, 13638, 13644, 13645, 13646, 13666,
        13672, 13673, 13674, 13695, 13701, 13702, 13703, 13790, 13796,
        13797, 13798, 13819, 13825, 13826, 13827, 13847, 13853, 13854,
        13855, 13876, 13882, 13883, 13884, 13971, 13977, 13978, 13979,
        14000, 14006, 14007, 14008, 14028, 14034, 14035, 14036, 14057,
        14063, 14064, 14065, 14152, 14158, 14159, 14160, 14181, 14187,
        14188, 14189, 14209, 14288, 14294, 14295, 14296, 14359, 14360,
        14361, 14362, 14363, 14364, 14370, 14371, 14372, 14440, 14441,
        14447, 14448, 14449, 14517, 14523, 14524, 14525, 14593, 14599,
        14600, 14601, 14669, 14675, 14676, 14677, 14745, 14751, 14752,
        14753, 14821, 14827, 14828, 14829, 14874, 14875, 14876, 14944,
        14950, 14951, 14952], dtype=int64),
 'product_mng': array([   66,    67,    68,    69,    71,    72,    73,    74,    75,
           76,   143,   144,   145,   146,   219,   220,   221,   222,
          296,   297,   298,   299,   372,   373,   374,   375,   448,
          449,   450,   451,   524,   525,   526,   527,   600,   601,
          602,   603,   676,   677,   678,   679,   752,   753,   754,
          755,   828,   829,   830,   831,   904,   905,   906,   907,
          980,   981,   982,   983,  1056,  1057,  1058,  1059,  1132,
         1133,  1134,  1135,  1209,  1210,  1211,  1212,  1286,  1287,
         1288,  1289,  1363,  1364,  1365,  1366,  1440,  1441,  1442,
         1443,  1517,  1518,  1519,  1520,  1593,  1594,  1595,  1596,
         1670,  1671,  1672,  1673,  1746,  1747,  1748,  1749,  1822,
         1823,  1824,  1825,  1898,  1899,  1900,  1901,  1974,  1975,
         1976,  1977,  2050,  2051,  2052,  2053,  2126,  2127,  2128,
         2129,  2202,  2203,  2204,  2205,  2278,  2279,  2280,  2281,
         2354,  2355,  2356,  2357,  2430,  2431,  2432,  2433,  2506,
         2507,  2508,  2509,  2583,  2584,  2585,  2586,  2660,  2661,
         2662,  2663,  2737,  2738,  2739,  2740,  2814,  2815,  2816,
         2817,  2891,  2892,  2893,  2894,  2967,  2968,  2969,  2970,
         3044,  3045,  3046,  3047,  3120,  3121,  3122,  3123,  3196,
         3197,  3198,  3199,  3272,  3273,  3274,  3275,  3348,  3349,
         3350,  3351,  3424,  3425,  3426,  3427,  3500,  3501,  3502,
         3503,  3576,  3577,  3578,  3579,  3652,  3653,  3654,  3655,
         3728,  3729,  3730,  3731,  3804,  3805,  3806,  3807,  3880,
         3881,  3882,  3883,  3957,  3958,  3959,  3960,  4034,  4035,
         4036,  4037,  4111,  4112,  4113,  4114,  4188,  4189,  4190,
         4191,  4265,  4266,  4267,  4268,  4341,  4342,  4343,  4344,
         4418,  4419,  4420,  4421,  4494,  4495,  4496,  4497,  4570,
         4571,  4572,  4573,  4646,  4647,  4648,  4649,  4722,  4723,
         4724,  4725,  4798,  4799,  4800,  4801,  4874,  4875,  4876,
         4877,  4950,  4951,  4952,  4953,  5026,  5027,  5028,  5029,
         5102,  5103,  5104,  5105,  5178,  5179,  5180,  5181,  5254,
         5255,  5256,  5257,  5331,  5332,  5333,  5334,  5408,  5409,
         5410,  5411,  5485,  5486,  5487,  5488,  5562,  5563,  5564,
         5565,  5639,  5640,  5641,  5642,  5715,  5716,  5717,  5718,
         5792,  5793,  5794,  5795,  5868,  5869,  5870,  5871,  5944,
         5945,  5946,  5947,  6020,  6021,  6022,  6023,  6096,  6097,
         6098,  6099,  6172,  6173,  6174,  6175,  6248,  6249,  6250,
         6251,  6324,  6325,  6326,  6327,  6400,  6401,  6402,  6403,
         6476,  6477,  6478,  6479,  6552,  6553,  6554,  6555,  6628,
         6629,  6630,  6631,  6705,  6706,  6707,  6708,  6782,  6783,
         6784,  6785,  6859,  6860,  6861,  6862,  6936,  6937,  6938,
         6939,  7013,  7014,  7015,  7016,  7089,  7090,  7091,  7092,
         7166,  7167,  7168,  7169,  7242,  7243,  7244,  7245,  7318,
         7319,  7320,  7321,  7394,  7395,  7396,  7397,  7470,  7471,
         7472,  7473,  7546,  7547,  7548,  7549,  7622,  7623,  7624,
         7625,  7698,  7699,  7700,  7701,  7774,  7775,  7776,  7777,
         7850,  7851,  7852,  7853,  7926,  7927,  7928,  7929,  8002,
         8003,  8004,  8005,  8079,  8080,  8081,  8082,  8156,  8157,
         8158,  8159,  8233,  8234,  8235,  8236,  8310,  8311,  8312,
         8313,  8387,  8388,  8389,  8390,  8463,  8464,  8465,  8466,
         8540,  8541,  8542,  8543,  8616,  8617,  8618,  8619,  8692,
         8693,  8694,  8695,  8768,  8769,  8770,  8771,  8844,  8845,
         8846,  8847,  8920,  8921,  8922,  8923,  8996,  8997,  8998,
         8999,  9072,  9073,  9074,  9075,  9148,  9149,  9150,  9151,
         9224,  9225,  9226,  9227,  9300,  9301,  9302,  9303,  9376,
         9377,  9378,  9379,  9453,  9454,  9455,  9456,  9530,  9531,
         9532,  9533,  9607,  9608,  9609,  9610,  9684,  9685,  9686,
         9687,  9761,  9762,  9763,  9764,  9837,  9838,  9839,  9840,
         9914,  9915,  9916,  9917,  9990,  9991,  9992,  9993, 10066,
        10067, 10068, 10069, 10142, 10143, 10144, 10145, 10218, 10219,
        10220, 10221, 10294, 10295, 10296, 10297, 10370, 10371, 10372,
        10373, 10446, 10447, 10448, 10449, 10522, 10523, 10524, 10525,
        10598, 10599, 10600, 10601, 10674, 10675, 10676, 10677, 10750,
        10751, 10752, 10753, 10827, 10828, 10829, 10830, 10904, 10905,
        10906, 10907, 10981, 10982, 10983, 10984, 10996, 10997, 10998,
        10999, 11073, 11074, 11075, 11076, 11088, 11089, 11090, 11091,
        11165, 11166, 11167, 11168, 11174, 11175, 11176, 11177, 11251,
        11252, 11253, 11254, 11264, 11265, 11266, 11267, 11341, 11342,
        11343, 11344, 11387, 11388, 11389, 11390, 11416, 11417, 11418,
        11419, 11444, 11445, 11446, 11447, 11473, 11474, 11475, 11476,
        11522, 11523, 11524, 11525, 11568, 11569, 11570, 11571, 11597,
        11598, 11599, 11600, 11625, 11626, 11627, 11628, 11654, 11655,
        11656, 11657, 11703, 11704, 11705, 11706, 11749, 11750, 11751,
        11752, 11778, 11779, 11780, 11781, 11806, 11807, 11808, 11809,
        11835, 11836, 11837, 11838, 11884, 11885, 11886, 11887, 11930,
        11931, 11932, 11933, 11959, 11960, 11961, 11962, 11987, 11988,
        11989, 11990, 12066, 12067, 12068, 12069, 12071, 12072, 12073,
        12074, 12075, 12076, 12143, 12144, 12145, 12146, 12219, 12220,
        12221, 12222, 12296, 12297, 12298, 12299, 12372, 12373, 12374,
        12375, 12448, 12449, 12450, 12451, 12524, 12525, 12526, 12527,
        12600, 12601, 12602, 12603, 12676, 12677, 12678, 12679, 12752,
        12753, 12754, 12755, 12809, 12810, 12811, 12812, 12885, 12886,
        12887, 12888, 12961, 12962, 12963, 12964, 13038, 13039, 13040,
        13041, 13115, 13116, 13117, 13118, 13192, 13193, 13194, 13195,
        13207, 13208, 13209, 13210, 13284, 13285, 13286, 13287, 13299,
        13300, 13301, 13302, 13376, 13377, 13378, 13379, 13385, 13386,
        13387, 13388, 13462, 13463, 13464, 13465, 13475, 13476, 13477,
        13478, 13552, 13553, 13554, 13555, 13598, 13599, 13600, 13601,
        13627, 13628, 13629, 13630, 13655, 13656, 13657, 13658, 13684,
        13685, 13686, 13687, 13733, 13734, 13735, 13736, 13779, 13780,
        13781, 13782, 13808, 13809, 13810, 13811, 13836, 13837, 13838,
        13839, 13865, 13866, 13867, 13868, 13914, 13915, 13916, 13917,
        13960, 13961, 13962, 13963, 13989, 13990, 13991, 13992, 14017,
        14018, 14019, 14020, 14046, 14047, 14048, 14049, 14095, 14096,
        14097, 14098, 14141, 14142, 14143, 14144, 14170, 14171, 14172,
        14173, 14198, 14199, 14200, 14201, 14277, 14278, 14279, 14280,
        14282, 14283, 14284, 14285, 14286, 14287, 14354, 14355, 14356,
        14357, 14430, 14431, 14432, 14433, 14507, 14508, 14509, 14510,
        14583, 14584, 14585, 14586, 14659, 14660, 14661, 14662, 14735,
        14736, 14737, 14738, 14811, 14812, 14813, 14814, 14934, 14935,
        14936, 14937], dtype=int64),
 'sales': array([    0,     1,     2, ..., 14969, 14970, 14971], dtype=int64),
 'support': array([   46,    47,    48, ..., 14996, 14997, 14998], dtype=int64),
 'technical': array([   35,    36,    37, ..., 14987, 14988, 14989], dtype=int64)}

sales_values = df["left"].iloc[dp_indices['sales']].values
technical_values = df["left"].iloc[dp_indices["technical"]].values
ss.ttest_ind(sales_values, technical_values)

Ttest_indResult(statistic=-1.0601649378624074, pvalue=0.2891069046174478)

ss.ttest_ind(sales_values, technical_values)[1]  # 只取p值

0.2891069046174478

# 如何两两求p值
dp_keys = list(dp_indices.keys())
dp_t_mat = np.zeros([len(dp_keys), len(dp_keys)])
for i in range(len(dp_keys)):
    for j in range(len(dp_keys)):
        p_value = ss.ttest_ind(df["left"].iloc[dp_indices[dp_keys[i]]].values,\
                              df["left"].iloc[dp_indices[dp_keys[j]]].values)[1]
        if p_value<0.05:
            dp_t_mat[i][j] = -1
        else:
            dp_t_mat[i][j] = p_value
sns.heatmap(dp_t_mat, xticklabels=dp_keys, yticklabels=dp_keys)
# 所有黑色部分都可以认为部门之间的离职率是有显著差异的，
# 其他颜色部分都可以认为部门之间的离职率是没有显著差异的

# 透视表交叉分析法
piv_tb = pd.pivot_table(df, values="left", index=["promotion_last_5years", "salary"],\
                       columns=["Work_accident"], aggfunc=np.mean)
piv_tb

	Work_accident	0	1
promotion_last_5years	salary
0	high	0.082996	0.000000
	low	0.331728	0.090020
	medium	0.230683	0.081655
1	high	0.000000	0.000000
	low	0.229167	0.166667
	medium	0.028986	0.023256

sns.heatmap(piv_tb, vmin=0, vmax=1)  # 颜色越浅离职率越高

# 换个颜色显示
# 颜色越深离职率越高
sns.set_context(font_scale=1.5)
sns.heatmap(piv_tb, vmin=0, vmax=1, cmap=sns.color_palette("Reds", n_colors=256)) 

4.9 分组分析方法与实现

接下来，让我们一起学习分组分析。

1.分组分析有两种不同的含义，第一种含义顾名思义就是将数据进行分组后再进行分析比较。分组分析还有一种含义就是根据数据的特征将数据进行切分，分成不同的组，使得组内成员尽可能靠拢，组间的成员尽可能远离。那么在这种情况下，如果我们指定了每一条数据的分组来计算，当未知分组的数据出现的时候，更精确的判断它是哪个分组，这个过程我们可以叫做分类。

2.那如果我们不知道分组，仅是想让数据尽可能的物以类聚，我们可以把这个过程叫做聚类，分类和聚类都是我们之后要讲到的机器学习或者数据建模的主要内容，所以这块我们以后再讲。我们先讲第一种含义的分组分析，即将数据进行分组后进行分析。分组分析一般要结合其他分析方法进行配合使用，从这个角度来讲分组分析更像是一种辅助手段而不是一种目的性的分析。那么之前我们讲对比分析、交叉分析的时候，都讲到过数据分组，可以更直观的发现数据中属性的差异。分组分析最常用到的具体手段就是钻取。钻取就是改变数据维度的层次，变换分析力度的过程，根据钻取方向的不同，可以分为向下钻取和向上钻取。

3.向下钻取就是展开数据，查看数据细节的过程。比如一门考试，每个班都是一个分组，我们知道每个班的平均成绩，如果我们进一步想知道每个班里，男生和女生分别的平均成绩是多少，这个过程就是向下钻取的过程。
4.那么向上钻取就是汇总分组数据的过程。比如我们知道每个人的分数，汇总成每个班的平均分，就是向上钻取的过程。再比如我们知道一个品牌汽车每天的销售额，然后汇总成每个月的销售额，以月为单位进行分析，也是向上赚取的过程。

5.离散属性的分组是比较容易的，而连续属性的分组在分组前需要进行离散化。当然在进行连续属性的离散化之前，我们需要先看一下数据分布是不是有明显的可以区分的标志。比如将数据从小到大排列后，有没有一个明显的分隔或者明显的拐点，如果有可以直接使用。这里说到的分割，实际上就是相邻两个数据的差，我们可以认为它是一阶差分，刚才说到的拐点就是二阶差分。

6.那么另外一个思路，连续属性的分组要尽可能满足，相同的分组比较聚拢，不同的分组比较分离的特点。所以我们可以用聚类的方法进行连续属性的分组。比如我们可以用k-means方法来进行指定分组数目的连续属性分组，如果考虑标注的话，我们也可以结合不纯度的检验指标Gini系数来进行连续数据的离散化分组。聚类我们在后续的文章中会介绍到，我们先来看衡量不纯度的指标，Gini系数的计算。

基尼系数的定义如上，这里D代表我们目标的标注，比如HR表中我们关注的是员工是否会离职，那么D就代表是否离职属性。C代表的相对对于我们关注的属性来说要比较和对比的属性。比如上图这张表中我们想衡量x相对于y来讲，是不是具有很好的区分度，我们就可以带入这个公式。

然后就可以求得Gini系数，在这里这个值（第一个式子的分子部分）表示目标标注，为Y1时X1有多少个，而分母表示Y1的个数，其他同理。我们来看上图中AB的例子。比如说标注为Y1时X1有两个，那么Count X1 | Y1 = 2,而Y1一共有3个所以Count Y1=3。其他同理可得。把这些数据带入就可以得到它的Gini系数。

那么连续值的Gini系数怎么进行计算？

我们需要先将表按照连续值的大小进行排序，然后相邻两两之间划定界限，分别确定分组值。比如这里我们确定X1和X2，如下：

比如这里我们确定X1和X2，然后分别计算Gini系数，取Gini系数最小的切分媒介。这样我们就可以根据目标标注将连续数值进行分组了。比如我们在图中0.1-0.2之间的位置进行一次切分，求它的GIni系数。然后在0.2-0.7之间再切分一次，以此类推。最后切分完毕再计算一次取最小值。我们可以看到在图中位置进行的切分，它的Gini系数可以得到0，就可以取到最小值了。所以我们就可以以0.75进行切分，将连续数据进行分组。根据不纯度进行分组，使用最多的是分类模型中决策树算法中的curt算法，我们后面细说。下面我们开始实战演示一下：

实战演示：

import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns
df = pd.read_csv("HR.csv")
sns.barplot(x="salary", y="left", hue="department", data=df)
plt.show()

sl_s = df["satisfaction_level"]
sns.barplot(range(len(sl_s)), sl_s.sort_values())
plt.show()

4.10 相关分析方法与实现

理论内容参考前面的4.4，皮尔逊相关系数和斯皮尔曼相关系数内容。

相关分析是衡量两组数据或者说两组样本分布趋势或者变化趋势大小的分析。相关分析最常用的就是我们之前讲过的相关系数进行分析。用相关系数直接衡量相关性的大小，最为直接和方便。相关系数参考前面4.4内容，这里不做说明，下面直接开始代码实现：

# 导包
import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_context(font_scale=1.5)
df = pd.read_csv("HR.csv")
sns.heatmap(df.corr())   # 计算相关系数，它会自动去掉离散的属性
plt.show()

# 来调一下颜色
sns.heatmap(df.corr(), vmin=-1, vmax=1, cmap=sns.color_palette("RdBu", n_colors=128))
plt.show()

我们可以根据图例看到,蓝色代表的是接近于1,红色代表接近于-1。颜色越蓝表明两个值正相关，越红说明负相关。

（1）我们刚才说的相关分析是用相关系数直接衡量连续值的相关性。离散属性的相关性如何衡量，这是一个问题。我们先分析一个特例，比如有个二类离散属性的相关性问题。二类离散属性也就是说它只有两个分类，一个是0，一个是1。比如像什么是与否的判断 有或者没有之类的属性值。这样二类属性就可以编码成0和1。

（2）二类属性是可以用皮尔逊相关系数来直接衡量相关性的大小的，大家可以放心的使用。二类属性和连续值属性的相关性，我们可以借鉴上一节课讲到的不纯度，来进行解决和计算。当然我们也可以直接把二类属性进行相关性的计算，但这样的话可能会有一些失真。

（3）多类离散属性的相关系数有些麻烦，如果多类离散属性都是定序数据的话，比如像什么low、median high之类的。我们就直接可以编码成0、1、2这些值，进行皮尔逊相关系数的计算。注意的是这样也是有失真的。

（4）另外更为一般的我们可以使用熵这个定义，进行离散属性的相关性系数的计算。我们先来介绍一下什么是熵，熵是用来衡量不确定性的一个值。其定义式如下：

它把一个属性，每一个值它出现的概率乘以log这个概率，把所有的这些值的这种转化加起来 得到它的熵。
那么这个值越接近于0，那么意味着它的不确定性越小。那么log值它的底数就决定了熵的单位，如果它的底数为二的话，那么商的单位就是我们比较熟悉的比特。

我们来像个例子，比如说有一个属性，它的分布是0和1，它的分布是0和1，也就是说它有两种备选值，但它只出现了一种值。它的分布是0和1，那么它的商根据这个公式算出来的就是0。
因为，0 * log0 = 0， 1 * log1 = 0。所以它的熵就是0。也就是说属性就已经可以确定了，它没有什么信息量。

我们再来看，比如有一个分布，它有两种备选值，两种备选值各占50%，
那么他的熵就是1/2×log2(1/2) + 1/2×log2(1/2) = -1,再取反得到1。也就是说如果它的分布是0.5，0.5的话那么它的熵就是1比特。

更为一般的 如果样本都属于一个类别，那么它的商就是0。反而如果样本的类别越多，而且它的分布越均匀那么它的信息熵就越大。

还有一个概念，条件熵的定义，如上图。即在X条件下，Y的熵即为X分布下对于Y分别计算商然后进行求和。另一个比较重要的概念是互信息，它是有实际意义的，Y的商代表了Y的不确定性程度。X的条件下Y的条件熵代表了X条件下Y的不确定性程度。因为加了分类的作用，所以就有了条件熵。条件熵相对于原来的熵一定是减少了。那么互信息的含义其实就是这个过程中减少的熵。另外有个性质，X和Y的互信息与Y和X的互信息是一样的。那么这个互信息我们也可以把它叫做信息增益。信息增益有一个比较大的缺点就是对于分类数目多的特征，它有不正确的偏向也就是说它不具有归一化的特点，它的不确定性是上不封顶的。这样对于我们分类的界定，或者是我们相关性的界定也是不方便的。

为了解决这个问题，我们可以定义这么一个值，熵的增益率。

那么X到Y的熵的增益率就是他们的互信息除以Y的熵。因为互信息一定是小于H(Y)的，所以这个值就是小于1的。而又由于商本来就是大于0的，所以这个值是大于0的，所以这个值是大于0的。但是如果直接用熵的增益率去衡量相关性的话，也是不妥的 这是因为熵的增益率它是不对称的，也就是说X对Y的熵的增益率和Y对X商的增益率是不一致的。所以我们需要进行一下转换，转换格式如上图第二个式子。

上面式子把分母换成X和Y熵的乘积再去开方，这个值还是0-1的，同样也满足了X和Y的对称性。下面我们看个例子：

有两个属性一个X，一个Y。怎么计算上面介绍的那些值。接下来，我们开始动手实践一下。

import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_context(font_scale=1.5)
df = pd.read_csv("HR.csv")

s1 = pd.Series(["X1", "X1", "X2", "X2", "X2", "X2"])
s2 = pd.Series(["Y1", "Y1", "Y1", "Y2", "Y2", "Y2"])
# 求熵
def getEntropy(s):
    if not isinstance(s, pd.core.series.Series):
        s = pd.Series(s)
    prt_ary = pd.groupby(s, by=s).count().values/float(len(s))  # 求出各部分概率
    return -(np.log2(prt_ary) * prt_ary).sum()
print("Entropy:", getEntropy(s1))

Entropy: 0.9182958340544896


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:7: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  import sys

print("Entropy:", getEntropy(s2))

Entropy: 1.0


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:7: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  import sys

# 条件熵
'''
这个图来解释是X1一共占了两个，所以它占整个的1/3，而在X1的分布下它的熵只有Y1
所以计算方法就是先计算X1情况下它的熵，然后再乘以1/3，X2同理。
Y1的熵是1/4 * log1/4 + 3/4 * log3/4，求和后结果再乘以2/3（X2所占比例）
上面两个加起来就是最后的条件熵。
'''
def getCondEntropy(s1, s2):
    d = dict()
    for i in list(range(len(s1))):  # s1值下s2分布
        d[s1[i]] = d.get(s1[i], []) + [s2[i]]
    return sum([getEntropy(d[k])*len(d[k])/float(len(s1)) for k in d]) 
    
print("EntropyGain", getCondEntropy(s1, s2))   # 可以交换参数看看结果

EntropyGain 0.5408520829727552


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:7: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  import sys

# 互信息
def getEntropyGain(s1, s2):
    return getEntropy(s2) - getCondEntropy(s1, s2)
print("EntropyGain:", getEntropyGain(s1, s2))  # 可以交换参数看看结果

EntropyGain: 0.4591479170272448


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:7: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  import sys

def getEntropyGainRatio(s1, s2):
    return getEntropyGain(s1, s2)/getEntropy(s2)
print("EntropyGainRatio:", getEntropyGainRatio(s1, s2)) # 可以交换参数看看结果

EntropyGainRatio: 0.4591479170272448


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:7: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  import sys

# 交换s1与s2,结果不对称
print("EntropyGainRatio:", getEntropyGainRatio(s2, s1))

EntropyGainRatio: 0.5


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:7: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  import sys

# 相关性
import math
def getDiscreteCorr(s1, s2):
    return getEntropyGain(s1, s2)/math.sqrt(getEntropy(s1) * getEntropy(s2))
print("DiscreteCorr:", getDiscreteCorr(s1, s2)) # 更换s1，s2结果不变，对称的

DiscreteCorr: 0.4791387674918639


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:7: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  import sys

# Gini系数
def getProbSS(s):
    if not isinstance(s, pd.core.series.Series):
        s = pd.Series(s)
    prt_ary = pd.groupby(s, by=s).count().values/float(len(s))
    return sum(prt_ary**2)
def getGini(s1, s2):
    d = dict()
    for i in list(range(len(s1))):
        d[s1[i]] = d.get(s1[i], []) + [s2[i]]
    return 1 - sum([getProbSS(d[k])*len(d[k])/float(len(s1)) for k in d])
print("Gini:", getGini(s1, s2))

Gini: 0.25


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:5: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  """

print("Gini:", getGini(s2, s1))  # 更换系数后不对称

Gini: 0.2222222222222222


D:\Anaconda3\lib\site-packages\ipykernel_launcher.py:5: FutureWarning: pd.groupby() is deprecated and will be removed; Please use the Series.groupby() or DataFrame.groupby() methods
  """

4.11 因子分析（成分分析）

因子分析就是从多个属性变量中，分析共性相关因子的方法。因子分析是个比较综合的分析方法，他几乎用到了我们这一章理论部分所有的知识点。

因子分析可以分为探索性因子分析和验证性因子分析。

探索性因子分析是指通过协方差矩阵相关性矩阵等指标，分析多元属性变量的本质结构并可以进行转化降维等操作，得到数据空间中或者影响目标属性的最主要因子。我们前面讲到的主成分分析法就是一种比较典型的探索性因子分析方法。

验证性因子分析是验证一个因子与我们关注的属性之间是否有关联，有什么样的关联，是不是符合我们的预期等等。验证性因子分析常用到我们之前说的假设检验、相关分析以及回归分析等等各种理论知识。

举个例子，比如说我们得到一张数据表，或者得到了非常多的属性，有的时候我们也会得到一个我们关注的目标属性或者标注。比如我们通过问卷调查的方式可以得到用户对某产品是否满意，还有像年龄性别等基本信息，还有各种生活习惯等个性的信息。如果我们关注用户对产品的满意情况，我们可以通过主成分分析，把除满意情况外全部的因子进行主成分降维，然后直接分析降维后因子与满意情况进行对比分析，就是探索性因子分析的一种方法。或者我们也可以不转化，直接来看相关矩阵，看哪个其他属性和我们关注的属性有比较强的关系，这也是一种探索性因子分析的思路。

如果我们换个角度，我们想看一下某个具体属性与满意度的关系，我们就会去验证这个属性和满意度是不是有关系，得到像相关性一致性之类的指标。或者我们直观上可以猜测某几个属性和满意度有关系。也可以用回归方法去拟合这几个属性与满意度的关联，根据误差大小来应验我们的假设是否准确。这些都是验证性因子分析的方法。接下来让我们进行一下简单的实践：

import pandas as pd
import numpy as np
import scipy.stats as ss
import matplotlib.pyplot as plt
import seaborn as sns

sns.set_context(font_scale=1.5)
df = pd.read_csv("HR.csv")

from sklearn.decomposition import PCA
my_pca = PCA(n_components=7)
lower_mat = my_pca.fit_transform(df.drop(labels=["salary", "department", "left"], axis=1))
print("Ratio:", my_pca.explained_variance_ratio_)
sns.heatmap(pd.DataFrame(lower_mat).corr(), vmin=-1, vmax=1, cmap=sns.color_palette("RdBu", n_colors=128))
plt.show()

Ratoo: [9.98565340e-01 8.69246970e-04 4.73865973e-04 4.96932182e-05
 2.43172315e-05 9.29496619e-06 8.24128218e-06]

小结

我们把以上知识总结了一个表格，如下：

探索性数据分析的内容，到这里就全部结束了。探索性数据分析就是狭义的数据分析的内容。本章节画图的代码自行运行观察结果，我是在本地记的笔记，上传到csdn就看不到画图的运行结果了。