2022济南大学acm新生赛题解
通过答题情况的难度系数:
签到:ABL
简单:DGKQ
中等:CMN
困难:EFHIJOPRST
A-和
算出n个数的和判断正负性即可!!!
发现很多同学的代码错误:要么sum未赋初值,要么数组大小定义太小导致数组溢出!!!
#include
#define ll long long
#define pb push_back
#define endl '\n'
#define close ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N=2e5+5;
void solve(){
int n;
cin>>n;
int sum=0;
while(n--){
int x;
cin>>x;
sum+=x;
}
if(sum==0) cout<<"zero"<0) cout<<"positive"< B-积
直接计算n个数的积的话,结果会导致爆long long,判断积的正负性只需找到负数的个数,如果出现了0,结果即0;否则如果出现负数的个数为偶数个,结果即为正数,否则即为负数!!
发现很多同学们的代码都直接算出n个数的积,结果会导致爆long long和int,故不能直接乘!
#include
using namespace std;
int main(){
int n,s=1,x;
cin>>n;
while(n--){
scanf("%d",&x);
if(x<0) s*=-1;
if(!x) s*=0;
}
puts(s>0?"positive":s?"negative":"zero");
} C-马
直接DFS或者BFS即可!!!
本来打算放这个基础搜索题目做个简单题,但是发现很多同学不会搜索,导致题目N过的人数也很少!!!
BFS做法:
#include
#define ll long long
#define pb push_back
#define endl '\n'
#define close ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N=2e5+5;
int vis[55][55][55];
struct node{
int x,y,z;
};
void solve(){
int n,m,h,t,stx,sty,stz;
cin>>n>>m>>h>>stx>>sty>>stz>>t;
vectord(t);
for(int i=0;i>d[i].x>>d[i].y>>d[i].z;
}
queueq;
q.push({stx,sty,stz});
int ans=0;
while(!q.empty()){
node u=q.front();
q.pop();
if(vis[u.x][u.y][u.z]) continue;
//cout<=1&&tx<=n)&&(ty>=1&&ty<=m)&&(tz>=1&&tz<=h)){
if(vis[tx][ty][tz]) continue;
q.push({tx,ty,tz});
}
}
}
cout<>_;
while(_--){
solve();
}
return 0;
}
DFS做法:
#include
using namespace std;
int a[31][3],ans,t,n,m,h;
bool f[51][51][51];
void dfs(int x,int y,int z){
f[x][y][z]=1,ans++;
for(int i=1;i<=t;i++){
int X=x+a[i][0],Y=y+a[i][1],Z=z+a[i][2];
if(X>0&&X<=n&&Y>0&&Z>0&&Y<=m&&Z<=h&&!f[X][Y][Z]) dfs(X,Y,Z);
}
}
int main(){
int x,y,z;
cin>>n>>m>>h>>x>>y>>z>>t;
for(int i=1;i<=t;i++) cin>>a[i][0]>>a[i][1]>>a[i][2];
dfs(x,y,z),cout< D-数
由题意可知,当n或m足够大的时候,总有一个值在[1,10]这个区间上,故可直接枚举大小更小的那个 集合作为二元有序对其中的一个数。例如:当集合A中的3时,集合B的大小为m(m>3),要满足此二元有序对,取集合m中大于3的数有m/3-1个,小于等于3的数可直接循环枚举!!!
发现一开始大部分同学都是直接O(n*m)暴力,学校oj判题都是直接把整个程序跑完,才判出TLE,导致oj直接爆了!!!一般的oj,1s钟可以跑4e8次左右,做题之前需先算出时间复杂度合不合适,再考虑实现代码!!!
#include
#define ll long long
#define pb push_back
#define endl '\n'
#define close ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N=2e5+5;
void solve(){
ll n,m;
cin>>n>>m;
if(n>m) swap(n,m);
ll ans=0;
for(int i=1;i<=n;i++){
ans+=m/i-1;
for(int j=1;j<=i;j++){
if(i%j==0) ans++;
}
}
cout< E-X限祖玛
在轮到玩家进行操作的时候,肯定是只要能选上连续X个相同颜色的祖玛球最优,故之间判断整个序列能操作的最大数max,max偶数即后者赢,否则前者赢!
#include
using namespace std;
const int N = 1e5 + 10;
char a[N];
int main() {
int n, x;
scanf("%d%d", &n, &x);
scanf("%s", a + 1);
pair stk[N];
int top = 0;
int cnt = 0;
for (int i = 1; i <= n; ) {
int j = i;
while (j <= n && a[i] == a[j]) j ++;
// [i, j - 1]
int stklen = 0;
if (top && stk[top].first == a[i])
stklen = stk[top].second;
int len = j - i + stklen;
cnt += len / x;
stk[++top] = {a[i], len - len / x * x};
if (top && stk[top].first == a[i]) {
while (top && stk[top].first == a[i]) top --;
}
if (len % x != 0)
stk[++top] = {a[i], len % x};
i = j;
}
if (cnt & 1)
puts("Fang is winner");
else
puts("Liang is winner");
} F-合成大魔棒
可发现所有树枝的价值小于等于1e9,故合并的次数最大是1000次,大于1000次,最后合成得到的值为负数,故不必考虑合成次数大于1000次的情况;
在考虑x次合并的时候,肯定是连续x+1合并得到的最大值最优,比如:1,2,3,4,5;此时合并两次,肯定是将后面连续3个数合并得到最大值12,如果2和3合并,4和5合并,此时最大值9,故无法保证此合并方案最优!
#include
#define ll long long
using namespace std;
const int Max=1e6+5;
int a[Max];
int pre[Max];
int ans=0;
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
// scanf("%d",&a[i]);
pre[i]=pre[i-1]+a[i];
}
int maxa=0;
for(int i=1;i<=min(1000,n);i++){
for(int j=1;j<=n;j++){
int r=j+i-1;
if(r>n) break;
maxa=max(maxa,pre[r]-pre[j-1]-(i-1)*(i-1)*(i-1));
}
}
cout< G-高铁路线规划
结论题:不能有三元环 那图必定是满二分图,所以题目变成求x+y=n 且xy最大,xy=x*(n-x),明显一个二次函数,取x=n/2的时候,x*(n-x)最大!!
#include
using namespace std;
int main(){
int n;
while(scanf("%d",&n)&&~n) printf("%d\n",n/2*(n-n/2));
} H-咕咕酱的饼
方法一:简单思维题,定义总面积为ans,如果向右移动,则加上此时向右移动增加的线段、线段两端向坐标轴做垂线与x轴组成的面积,如果向左移动,则减去此时向左移动增加的线段、线段两端向坐标轴做垂线与x轴组成的面积,向上,向下移动,更新此时的纵坐标y!
#include
#define ll long long
using namespace std;
int main(){
int n,x=0,y=0,z;
ll ans=0;
char s[1];
cin>>n;
while(n--){
scanf("%s%d",s,&z);
if(s[0]=='W') y+=z;
if(s[0]=='S') y-=z;
if(s[0]=='A') x-=z,ans-=1ll*z*y;
if(s[0]=='D') x+=z,ans+=1ll*z*y;
}
cout< 方法二:直接求多边形面积也行,可参考这篇博客了解多边形面积的求法:多边形面积计算_计算多边形面积_GISVertex的博客-CSDN博客
#include
#define ll long long
using namespace std;
const int Max=1e6+5;
struct node{
ll x,y;
};
node W[100];
int w=0,a=0,s=0,d=0;
int main(){
int n;
cin>>n;
ll x=0,y=0;
double ans=0;
W[0]={0,0};
for(int i=1;i<=n;i++){
char ch;ll num;
cin>>ch>>num;
ll nx,ny;
if(ch=='W'){//上
nx=x;ny=y+num;
W[++w]={nx,ny};
}else if(ch=='S'){//下
nx=x;ny=y-num;
W[++w]={nx,ny};
}else if(ch=='A'){//左
nx=x-num;ny=y;
W[++w]={nx,ny};
}else{//右
nx=x+num;ny=y;
W[++w]={nx,ny};
}
x=nx;y=ny;
}
for(int i=0;i I-咕咕酱的密码锁
简单思维题,其中存在某一行或者某一列的按钮不被按下,故这一行(一列)的增加的数字只能是列(行)的按钮所增加的,故根据给出未按下的行(列)就可以直到列(行)增加的次数,剩下的数即是行(列)增加的次数!!
#include
#define ll long long
using namespace std;
const int Max=1e6+5;
int a[Max],b[Max];
int room[105][105];
int main(){
int n,m;
cin>>n>>m;
char ch;int p;
cin>>ch>>p;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>room[i][j];
}
}
if(ch=='R'){
for(int i=1;i<=m;i++){
a[i]=room[p][i];
for(int j=1;j<=n;j++){
room[j][i]-=a[i];
}
}
for(int i=1;i<=n;i++) b[i]=room[i][1];
}else{
for(int i=1;i<=n;i++){
b[i]=room[i][p];
for(int j=1;j<=m;j++){
room[i][j]-=b[i];
}
}
for(int i=1;i<=m;i++) a[i]=room[1][i];
}
for(int i=1;i<=n;i++) cout< J-生徒会主席的竞选
背包dp,定义dp[i][j]为前i个人有效票产生j张的最小原始票数,转移方程:
dp[i][j]=min(dp[i-1][j-a[i]]+a[i]/2+1,dp[i][j]);#include
#define ll long long
using namespace std;
const int Max=1e6+5;
int a[Max];
int dp[1005][1005];
int main(){
int n;
cin>>n;int sum=0;
for(int i=1;i<=n;i++) cin>>a[i],sum+=a[i];
for(int i=0;i<=1000;i++){
for(int j=0;j<=1000;j++) dp[i][j]=1e9;
}
for(int i=0;i<=n;i++)
dp[i][0]=0;
for(int i=1;i<=n;i++){
for(int j=0;j<=1000;j++){
dp[i][j]=dp[i-1][j];
if(j-a[i]>=0) dp[i][j]=min(dp[i-1][j-a[i]]+a[i]/2+1,dp[i][j]);
// cout< K-Syan的最大值
容易知道将全部数字进行或操作最优!
这题过的人数很少,出乎我们意料,可能大部分同学没有接触过位运算,学过计组之后可能会更清楚一些,但是后面我们加上了样例解释,还是很多同学不敢做,其实第一位同学提交的代码思路完全正确,只是数组开太小导致溢出,不知为何放弃做这题了 !一般看到评测结果运行错误,大概率原因就是数组开小导致溢出!
#include
using namespace std;
const int N=1e5+5;
int a[N];
int main() {
int n;cin>>n;
int ans=0;
for(int i=1;i<=n;i++){
cin>>a[i];
ans|=a[i];
}
cout< L-Syan的无限循环小数(easy)
如题意可知,给出的a,b都在[1,5]这个区间,可直接手动枚举知道1/3,2/3,4/3,5/3是无线循环小数!
#include
using namespace std;
int main() {
int a,b;
cin>>a>>b;
if(a==1&&b==3) printf("YES\n");
else if(a==2&&b==3) printf("YES\n");
else if(a==4&&b==3) printf("YES\n");
else if(a==5&&b==3) printf("YES\n");
else printf("NO\n");
} M-Syan的无限循环小数(hard)
这题不同于L,给出的a,b都在[1,1000000000]这个区间,不可直接手动枚举,这时就需要知道这结论:将分数化为最简分数后,分母的全部因数(除去1和其自身)没有为2或5以外的数,则该分数就不是无限循环小数;否则为无限循环小数。
#include
using namespace std;
int main() {
int a, b;
cin >> a >> b;
int g = __gcd(a, b);
a /= g, b /= g;
if (a % b == 0)
puts("NO");
else {
while (b % 2 == 0)
b /= 2;
while (b % 5 == 0)
b /= 5;
puts(b == 1 ? "NO" : "YES");
}
} N-Syan的最大金币数
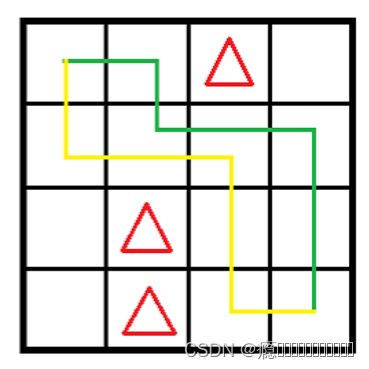
由题意可知,玩家可以从起点无数次到达终点,直到迷宫中可取的金币全部获得。从起点到达一个方格,如若想到获得迷宫中的金币,就必须再从此处到达终点,走出迷宫,例如样例
当走到(3,1)处时,此时只能往(4,1)和(3,2)走,但是(3,2)有障碍不能到达,走到(4,1)也是死路,故(3,1)处的金币无法获得!!!
故只需判断从起点(1,1)往终点(n,m)走,从终点(n,m)往起点(1,1)走,如果这两个方向都能到达一个方格,则此时的金币即可获得,做两次BFS即可!!!
#include
using namespace std;
#define sc(x) scanf("%d",&x)
#define sl(x) scanf("%lld",&x)
#define ll long long
#define pb push_back
const int Max=1e6+5;
const int Mod=998244353;
const int mod=998244353;
bool vis[1005][1005];
struct node{
int x,y;
};
int dir[2][2]={1,0,0,1};
bool flag[1005][1005];
int n;int m;
bool check(int x,int y){
if(x>=1&&x<=n&&y>=1&&y<=n) return true;
return false;
}
void bfs(int start_x,int start_y){
node start,next;
queueq;
q.push({start_x,start_y});
flag[start_x][start_y]=true;
while(!q.empty()){
start=q.front();
q.pop();
for(int i=0;i<2;i++){
next.x=start.x+dir[i][0];
next.y=start.y+dir[i][1];
if(check(next.x,next.y)&&!vis[next.x][next.y]&&!flag[next.x][next.y]){
q.push(next);
flag[next.x][next.y]=true;
}
}
}
}
bool flag1[1005][1005];
int dir1[2][2]={-1,0,0,-1};
void bfs1(int start_x,int start_y){
node start,next;
queueq;
q.push({start_x,start_y});
flag1[start_x][start_y]=true;
while(!q.empty()){
start=q.front();
q.pop();
for(int i=0;i<2;i++){
next.x=start.x+dir1[i][0];
next.y=start.y+dir1[i][1];
if(check(next.x,next.y)&&!vis[next.x][next.y]&&!flag1[next.x][next.y]){
q.push(next);
flag1[next.x][next.y]=true;
}
}
}
}
int main(){
cin>>n>>m;
for(int i=1;i<=m;i++){
int x,y;
cin>>x>>y;
vis[x][y]=true;
}
bfs(1,1);
bfs1(n,n);
int ans=0;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(i==1&&j==1) continue;
if(flag[i][j]&&flag1[i][j]) ans++;
}
}
cout< O-Syan的三元组
这题提交的人也有很多直接O(n*n*n)直接暴力,没有实现算明白时间复杂度!!!
方法一: 由D=|a-b|+|b-c|+|a-c|可知,当a=b=c的时候,距离最小,其余情况:
可知
L1=|a-b|; L1=|b-c|; L3=|a-c|;
D=|a-b|+|b-c|+|a-c|=L1+L2+L3=2L3;
由D的表达式可知,事实上决定D大小的关键时a和c的距离,于是问题就可以简化为每次固定c找一个a,使得L3=|c-a|最小;
#include
using namespace std;
const int N=1e5+5;
int a[N],b[N],c[N];
int main() {
int n;cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
cin>>b[i];
}
for(int i=1;i<=n;i++){
cin>>c[i];
}
sort(a+1,a+1+n);
sort(b+1,b+1+n);
sort(c+1,c+1+n);
int i=1,j=1,k=1;
long long ans=1e18;
while(i<=n&&j<=n&&k<=n){
long long D=abs(a[i]-b[j])+abs(b[j]-c[k])+abs(a[i]-c[k]);
ans=min(ans,D);
if(a[i]<=b[j]&&a[i]<=c[k]) i++;
else if(b[j]<=a[i]&&b[j]<=c[k]) j++;
else k++;
}
printf("%lld\n",ans);
} 方法二:也可以固定中间b的值,然后在a,c数组中二分找到距离b最近的一个值!!!
(附上王逸鸣学长的代码)
#include
#define ll long long
#define pb push_back
#define endl '\n'
#define close ios::sync_with_stdio(false),cin.tie(0)
using namespace std;
const int N=2e5+5;
void solve(){
int n;
cin>>n;
sets1,s2,s3;
for(int i=0;i>x;
s1.insert(x);
}
for(int i=0;i>x;
s2.insert(x);
}
for(int i=0;i>x;
s3.insert(x);
}
ll ans=3e10;
for(auto i:s1){
auto j=s2.lower_bound(i),k=s3.lower_bound(i);
if(j==s2.end()||k==s3.end()) continue;
ans=min(ans,abs(i-*j)+abs(i-*k)+abs(*j-*k));
}
for(auto j:s2){
auto i=s1.lower_bound(j),k=s3.lower_bound(j);
if(i==s1.end()||k==s3.end()) continue;
ans=min(ans,abs(*i-j)+abs(*i-*k)+abs(j-*k));
}
for(auto k:s3){
auto j=s2.lower_bound(k),i=s1.lower_bound(k);
if(j==s2.end()||i==s1.end()) continue;
ans=min(ans,abs(*i-*j)+abs(*i-k)+abs(*j-k));
}
cout< P-Shiki的二元组
二分找第k个小的数,check判断二分此时的mid前面有几个比其小的数!
这题新生做之前可能还有很多同学没有接触二分!
#include
using namespace std;
#define sc(x) scanf("%d",&x)
#define sl(x) scanf("%lld",&x)
#define ll long long
#define pb push_back
const int Max=1e6+5;
const int Mod=998244353;
ll a[Max],b[Max];
int main(){
int n;sc(n);
ll k;sl(k);
for(int i=1;i<=n;i++) sl(a[i]);
for(int i=1;i<=n;i++) sl(b[i]);
sort(a+1,a+1+n);
sort(b+1,b+1+n);
ll l=0,r=1e18;
ll x=0;
while(l<=r){
ll mid=(l+r)/2;
ll ans=0;
bool flag=false;ll sum;
for(int i=1;i<=n;i++){
// if(flag) break;
if(a[i]*b[n]<=mid) ans+=n;
else{
int L=1,R=n;
while(L<=R){
int Mid=(L+R)/2;
if(a[i]*b[Mid]>mid) R=Mid-1;
else L=Mid+1;
}
// cout< Q-被守护者的灵柩
直接判断t是否是s的子序列,时间复杂度O(n*n)。循环t字符串,找到t[1]第一次出现在s的位置,然后依次找t[i](在t[i-1]出现在s的位置之后出现t[i]的第一个位置,i>1).
#include
#define ll long long
using namespace std;
const int Max=1e6+5;
char a[Max],b[Max];
int main(){
scanf("%s",a+1);
scanf("%s",b+1);
int len=strlen(b+1);
int len_a=strlen(a+1);
int j=1;
bool flag=true;
for(int i=1;i<=len;i++){
while(j<=len_a&&b[i]!=a[j]){
j++;
}
if(b[i]==a[j]) j++;
else{
flag=false;break;
}
}
if(flag) printf("yes\n");
else printf("no\n");
} R-千手百眼 天下人间
本题考查裴蜀定理:若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别的,一定存在整数x,y,使得ax+by=d成立。
具体证明可参考这篇博客:裴蜀定理_Hypoc_的博客-CSDN博客
故这题只需计算n个数的gcd,然后判断这是否是m的因子即可!
#include
#define ll long long
using namespace std;
const int Max=1e6+5;
int a[Max],b[Max];
mapmp;
int main(){
int n;cin>>n;int m;cin>>m;m=abs(m);
cin>>a[1];
int num=a[1];
for(int i=2;i<=n;i++){
cin>>a[i];
num=__gcd(num,a[i]);
}
if(m%num==0) printf("yes\n");
else printf("no\n");
} S-流转存续的花神诞祭(dp)
方法一:定义状态dp[i]表示到达梦境i的方案数,pre_a[i]表示前i个梦境的推理难度和,pre_b[i]表示前i个梦境的梦境深度和,梦境i能到达的i+1~i+k,状态转移方程为
dp[i+1~i+k]+=dp[i]很显然,这就变成了单点询问+区间修改问题,利用树状数组维护即可!
每个梦境i能到达的最大梦境i+k可以前缀和+二分求得k
#include
#define ll long long
using namespace std;
const int Max=1e6+5;
const ll INF=1e15+5;
const ll mod=998244353;
ll n,x,y;
int lowbit(int x){
return x&-x;
}
long long tree[Max];
void update(int x,ll y){
while(x<=n){
tree[x]+=y;
x+=lowbit(x);
}
}
long long getsum(int x){
long long sum=0;
while(x){
sum+=tree[x];
x-=lowbit(x);
}
return sum%mod;
}
ll pre_a[Max],pre_b[Max];
ll a[Max],b[Max];
int main(){
scanf("%lld%lld%lld",&n,&x,&y);
for(int i=1;i<=n;i++){
scanf("%lld%lld",&a[i],&b[i]);
pre_a[i]=pre_a[i-1]+a[i];
pre_b[i]=pre_b[i-1]+b[i];
}
for(int i=0;i<=n;i++){
int l=i+1,r=n,X=-1;
while(l<=r){
int mid=(l+r)/2;
if(pre_a[mid]-pre_a[i]>x||pre_b[mid]-pre_b[i]>y) r=mid-1;
else{
X=mid,l=mid+1;
}
}
if(X==-1) continue;
ll ans=1;
if(i) ans=getsum(i);
update(i+1,ans);
update(r+1,-ans);
}
printf("%lld\n",getsum(n));
} 方法二:前缀和+dp
定义状态f[i]表示到达前i个梦境的方案数,问题转化为第i个梦境可能由第i-k~i-1个梦境转移过来,第i个梦境可能是[i-k,i-1]转移过来,那么第i+1个梦境最大区间范围只可能是在第i个梦境区间[i-k,i-1]的基础上加上第i个,这样就是[i-k,i],如果不满足推理难度<=x和梦境深度<=y,一个一个删除区间最左边的值,直到符合推理难度<=x和梦境深度<=y,第i+2个梦境在第i+1个梦境的基础以此类推得到转移方程
f[i]=((s?f[i-1]-f[s-1]:f[i-1])+1ll*f[i-1])%mod;#include
using namespace std;
const int N=5e5+5,mod=998244353;
long long a[N],b[N],f[N];
int main(){
int n,X,Y,s=0,s1=0,s2=0;
scanf("%d%d%d",&n,&X,&Y),f[0]=1;
for(int i=1;i<=n;i++) scanf("%lld%lld",&a[i],&b[i]);
for(int i=1;i<=n;i++){
s1+=a[i],s2+=b[i];
while(s1>X||s2>Y) s++,s1-=a[s],s2-=b[s];
f[i]=((s?f[i-1]-f[s-1]:f[i-1])+1ll*f[i-1])%mod;
}
printf("%d\n",(1ll*f[n]-f[n-1]+mod)%mod);
} T-命运尽头的垂泪者
模拟题,按照题意模拟即可!
#include
using namespace std;
#define sc(x) scanf("%d",&x)
#define sl(x) scanf("%lld",&x)
#define ll long long
#define pb push_back
const double esp=1e-8;
const int Max=1e6+5;
const int Mod=998244353;
ll a[Max],b[Max];
queueq;
int main(){
int n;
double h,m,k;
cin>>n>>h>>m>>k;
double M=m,H=h;
double st_cao=0;double cao=0;
for(int i=1;i<=n;i++){
cao-=st_cao;
string str;
double cnt,dmg;
cin>>str;
if(str=="Physico") cin>>dmg;
else cin>>cnt>>dmg;
if(str=="Anemo"){//风
m-=0.5*cnt;
m-=0.2*M*dmg/H;
}else if(str=="Geo"){//岩
m-=0.5*cnt;
m-=0.2*M*dmg/H;
}else if(str=="Electro"||str=="Pyro"){//雷火
if(str=="Pyro") m-=2*cnt;
else m-=cnt;
m-=0.2*M*dmg/H;
int len=q.size();
len=min(len,2);
m-=0.2*6*k*len*M/H;
while(!q.empty()) q.pop();
}else if(str=="Dendro"){//草
m-=0.2*M*dmg/H;
if(cao>esp){
cao=max(cao,0.8*cnt);
}else{
cao=0.8*cnt;
st_cao=1.6*cnt/(14+5*cnt);
}
}else if(str=="Hydro"){//水
m-=0.2*M*dmg/H;
if(cao>esp){
cao-=0.5*cnt;
q.push(i);
}
}else if(str=="Cryo"){//冰
}else if(str=="Physico"){//物理
m-=0.2*M*dmg/H;
}
}
while(!q.empty()){
if(n-q.front()==6){
m-=0.2*M*4*k/H;;
// h-=4*k;
}q.pop();
}
double sum=m*100.0/M;
if(sum>esp) printf("%.2lf%%\n",sum);
else printf("win\n");
}