力扣20 - 有效的括号【暴力、分支判断、哈希表】
有关这道力扣上的题,通过反复思考和资料查询,为大家总结出了这三种解法,分别是暴力解法、分支判断以及哈希表,在LeetCode上都可以AC
文章目录
- 题目描述
- 解法一:暴力解法
-
- 思路分析
- 解法二:分支判断
-
- 多重情况分析
- 思路解析
- 解法三:哈希表
-
- 思路推理
- 方案解析
- 解法四、底层实现(C语言版补充)
-
- 1、整体代码展示
- 2、代码讲解
- 总结
力扣题目链接
题目描述
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
1、左括号必须用相同类型的右括号闭合。
2、左括号必须以正确的顺序闭合。
示例1
输入: “()”
输出: true
示例2
输入:s = “()[]{}”
输出:true
示例3
输入:s = “(]”
输出:false
示例4
输入:s = “([)]”
输出:false
示例5
输入:s = “{[]}”
输出:true
解法一:暴力解法
- 对于这道题,我一开始做的时候就想着这是一个堆栈结构,通过不断地将即将入栈的元素和栈中的栈顶元素进行判断,从而来决定保留还是出栈,因此直接衍生出这么一段暴力代码
class Solution {
public:
bool isValid(string s) {
stack<char> t;
for(int i=0;i<s.size();++i)
{
if(t.empty())
{
t.push(s[i]);
continue;
}
char m_top=t.top();
if(s[i]=='}' && m_top=='{')
{
t.pop();
continue;
}
else if(s[i]==']' && m_top=='[')
{
t.pop();
continue;
}
else if(s[i]==')' && m_top=='(')
{
t.pop();
continue;
}
t.push(s[i]);
}
return t.empty();
}
};
思路分析
- 首先,是开辟了一个栈的容器空间,这是C++中STL的一个容器,因此可以直接拿来使用,如果有小伙伴不了解STL人弄起,可以看一下我写的这篇博客,介绍得很详细哦 C++STL容器详解,接着,就进行判断,如果栈为空,就继续往里面入元素,这里的continue就是强制进入下一个循环,也就是操作完一个元素就跳出本循环,然后进行下一个循环元素的判断,然后,就是对每一次将要入栈的元素进行判断,如果和前面一个括号相互匹配,那就将其出栈,并且也跳出循环,判断下一元素。并且在每一次判断结束后都要再入栈一个新的元素以此可以进行下一次判断,最后返回**t.empty()**是因为如果容器中无元素,即说明栈中的元素和入栈的元素均匹配成功,返回的便是true或false;
代码千万条,暴力第一条;暴力不规范,编译两行泪
虽然有时候暴力解法还是挺管用的,一个个列出所要求的情况,但是这样所带来的便是时间复杂度的提升,有时候直接上两层for循环就是O(n2)的复杂度,还有一个就是暴力很容易导致超时,用过暴力刷题的小伙伴都清楚,所以我们还是尽量避免用暴力,尽量想出一些最优解,实在想不出来才用暴力。下面两种是我想出来的其他两种方案,大家可以仔细看看;
解法二:分支判断
多重情况分析
首先,来分析一下三种不同的情况
第一种 匹配结束,仍有括号剩余没有匹配(已进栈),因此栈不为空
第二种 在匹配过程中,发现无与之匹配的前括号
第三种 在匹配过程中,栈外(没进栈)有括号冗余,但此时栈空了,无法寻找与之匹配的对象
class Solution {
public:
//分析
//1.匹配结束,仍有括号剩余没有匹配(已进栈),因此栈不为空
//2.在匹配过程中,发现无与之匹配的前括号
//3.在匹配过程中,栈外(没进栈)有括号冗余,但此时栈空了,无法寻找与之匹配的对象
bool isValid(string s) {
stack<char> st;
for(int i=0;i<s.size();++i)
{
if(s[i]=='(') st.push(')');
else if(s[i]=='[') st.push(']');
else if(s[i]=='{') st.push('}');
//2.在匹配过程中,发现无与之匹配的前括号
//3.在匹配过程中,栈外(没进栈)有括号冗余,但此时栈空了,无法寻找与之匹配的对象
else if(st.empty() || st.top()!=s[i]) return false;
else st.pop();
}
//1.匹配结束,仍有括号剩余没有匹配(已进栈),因此栈不为空
return st.empty();
}
};
思路解析
- 首先一样是对进栈的字符串进行遍历循环,然后在循环内判断会遇到的三种不同的括号以及在匹配过程中会出现的匹配不成功的方案,即无与之匹配的前括号以及栈外的元素想要入栈匹配,但是栈内已经为空的情况,如果都不满足以上的情况,则出栈栈顶元素,最后一种仍有括号剩余没有匹配,但此时栈为空的情况,这需要在匹配结束后进行判断,因此返回栈的empty()值;
解法三:哈希表
思路推理
这里再详细演示一遍推理的思路,还有不懂的小伙伴可以再理一理
①首先入栈大括号{(左)
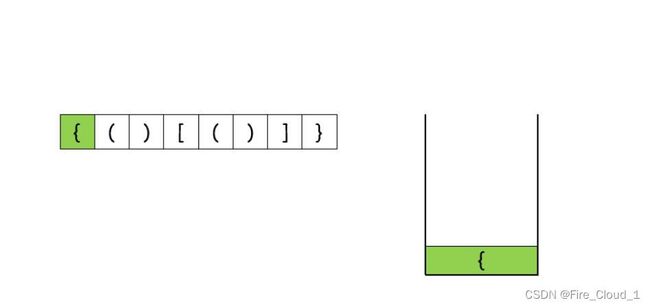
②然后入栈小括号(左)
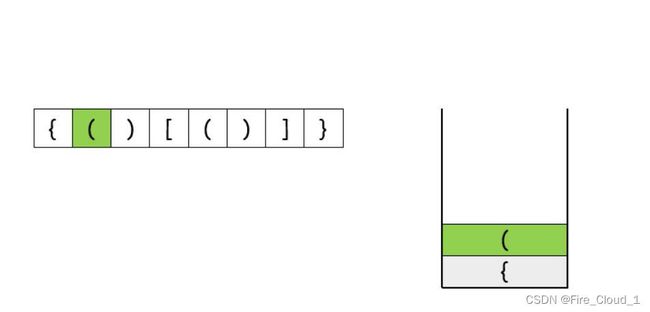
③接着即将入栈小括号)(右),[先进行判断,此时还没有入栈],从而判断出与刚才的形成了一对,那之前入栈的左小括号便出栈

④入栈中括号[(左)
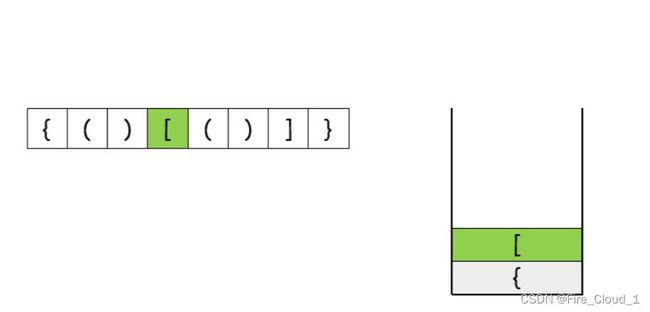
⑤入栈小括号((左)
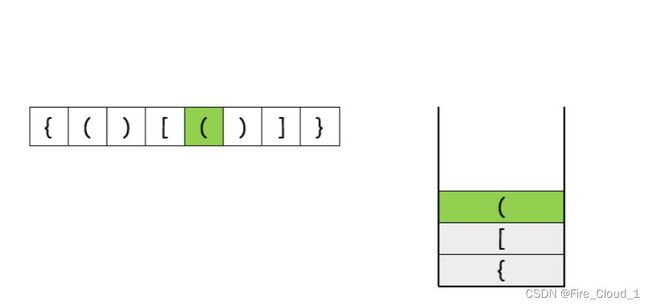
⑥同理,这里的右小括号与上一个左小括号形成配对,故左小括号出栈

⑦这里的右中括号与上一个左中括号形成配对,故左中括号出栈

⑧此时栈中只剩下一个大左括号,与即将入栈的大有括号又形成了配对,所以大左括号出栈
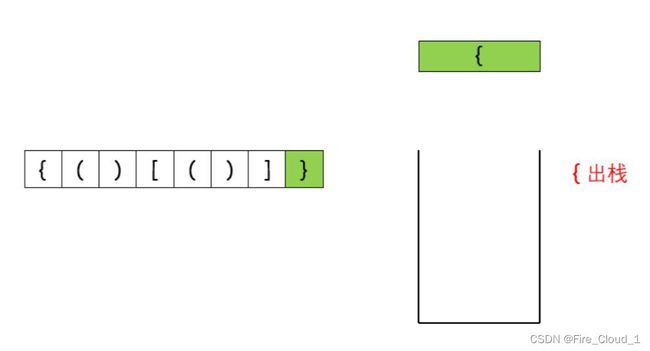
⑨最后全部元素均出栈,因此栈为空,st.empty()返回的便是true;

方案解析
先给出代码:
class Solution {
public:
bool isValid(string s) {
unordered_map<char,int> m{{'(',1},{'[',2},{'{',3},
{')',4},{']',5},{'}',6}};
stack<char> st;
bool istrue=true;
for(char c:s){
int flag=m[c];
if(flag>=1&&flag<=3) st.push(c);
else if(!st.empty()&&m[st.top()]==flag-3) st.pop();
else {istrue=false;break;}
}
if(!st.empty()) istrue=false;
return istrue;
}
};
接下来讲解一下:
- 这里的话是用到了unordered_map,也是属于C++STL中的一组容器,也是常见的哈希结构中的一种,也可以设定它的key值和value值,这里是设定了六组,因为三种括号分别有两个,key值是char类型,用来保存字符,value值是int类型,用来保存有多少种类的符号。
- 就这就定义了一个bool类型的值,将其初始值设置为true,用于判断括号是否匹配成功,接着进入循环,顶一个flag用于保存当前匹配到的括号种类,flag>=1&&flag<=3说明即将入栈的只是前括号,无后括号与之匹配,因此需要push(),m[st.top()] == flag-3表明后面匹配的符号与flag值为1~3区间内的符号是否相同,若是相同以及栈不为空,则将其出栈,最后,如果字符串都匹配完了还是没有配对成功,即istrue=false,那就break跳出循环;
解法四、底层实现(C语言版补充)
两个月前做的这道题,前几天又看到,用C实现了一遍,故而做一个补充
1、整体代码展示
typedef int STDateType;
typedef struct Stack {
STDateType* a; //栈元素
int top; //栈顶指针
int capaity; //容量
}ST;
void InitStack(ST* s);
void DestoryStack(ST* s);
void Push(ST* s,STDateType x);
void Pop(ST* s);
bool StackEmpty(ST* s);
STDateType Top(ST* s);
int StackSize(ST* s);
bool isValid(char * s){
ST st;
InitStack(&st);
while(*s)
{
//1.若为左括号,则入栈
if((*s == '(')
|| (*s == '{')
|| (*s == '['))
{
Push(&st,*s);
++s;
}
else //2.若为有括号,则进行判断匹配
{
//若匹配到右括号后无左括号与之匹配,返回false
if(StackEmpty(&st))
return false;
STDateType top = Top(&st);
Pop(&st);
if(top == '(' && *s != ')'
|| top == '{' && *s != '}'
|| top == '[' && *s != ']')
{
DestoryStack(&st);
return false;
}
else
++s;
}
}
//若在匹配完成后栈不为空,则表示还要括号没有完成匹配
if(!StackEmpty(&st))
return false;
DestoryStack(&st);
return true;
}
/*初始化栈*/
void InitStack(ST* s)
{
/**
* 初始化时,top给的是0,意味着top指向栈顶数据的下一个
* 初始化时,top给的是-1,意味着top指向栈顶数据
*/
assert(s);
s->a = NULL;
s->top = 0; //先入栈再后移栈顶指针
//s->top = -1; 先移栈顶指针再入栈
s->capaity = 0;
}
/*销毁栈*/
void DestoryStack(ST* s)
{
assert(s);
free(s->a);
s->a = NULL;
s->top = s->capaity = 0;
}
/*入栈*/
void Push(ST* s,STDateType x)
{
assert(s);
//判断栈满的情况
if (s->top == s->capaity)
{
//若栈满,则执行扩容
int newCapacity = s->capaity == 0 ? 4 : s->capaity * 2;
//STDateType* tmp = (STDateType*)malloc(sizeof(STDateType*) * newCapacity);
STDateType* tmp = (STDateType*)realloc(s->a, sizeof(STDateType) * newCapacity);
if (tmp == NULL)
{
printf("realloc fail\n");
exit(-1);
}
//更新扩容后的栈数据
s->a = tmp;
s->capaity = newCapacity;
}
s->a[s->top] = x;
s->top++;
}
/*出栈*/
void Pop(ST* s)
{
assert(s);
assert(s->top > 0);
s->top--;
}
/*判断栈是否为空*/
bool StackEmpty(ST* s)
{
return s->top == 0;
}
/*取栈顶元素*/
STDateType Top(ST* s)
{
assert(s);
assert(!StackEmpty(s));
return s->a[s->top - 1];
}
/*求栈大小*/
int StackSize(ST* s)
{
assert(s);
return s->top;
}
2、代码讲解
- 主要看到是中间那一段,第一段是一些结构体以及函数的声明,第三段是堆栈的原理实现
- 实行的思路很简单,就是去判断入栈的符号为左括号还是右括号,若为左括号,则入栈,若为右括号,则取出当前栈顶元素与当前字符串所匹配的括号进行三种组合的匹配,若是没有一种成立,则返回false,这里要注意的是别忘了DestroyStack(),因为提前返回了false的话就执行不到最后一句了,不释放堆栈会造成内存泄漏,当然力扣里看不出来
- 然后的话就是对几种特殊情况的判断
- 先是第一种,也就是整个匹配结束后栈里面还有元素存留,说明括号没有匹配完成,返回false
- 然后是第二种,就是当你匹配到右括号时栈中却没有左括号与之匹配,这时判断栈是否为空就好了,若栈为空,则表示栈中没有括号,也就是这段代码
//若匹配到右括号后无左括号与之匹配,返回false
if(StackEmpty(&st))
return false;
- 最后一种的话就是在匹配不成功时返回false的那种,具体见如上代码
总结
以上就是对于【力扣20.有效的括号】的三种解法,分别是暴力、分支和哈希,其中还是分支判断比较好理解一下,哈希表的话效率较高一些,可以做提升,暴力的话不太推荐,看一遍就行,这种自己也能写出来。好啦,最后谢谢您对本文的观看,如果觉有有什么问题请于评论区留言或者私信我都可以,觉得写的还可以的话就留下你的小红心吧❤️


