蓝桥杯C/C++B组历届真题刷题【合集】

蓝桥杯历届真题刷题C语言网 【小技巧：可改page=？快速跳转】

2012年及以前蓝桥杯大赛历届真题（共14题）

1434 蓝桥杯历届试题-回文数字【简易法判断回文】

时间限制: 1Sec 内存限制: 128MB
题目描述
观察数字：12321，123321 都有一个共同的特征，无论从左到右读还是从右向左读，都是相同的。这样的数字叫做：回文数字。

本题要求你找到一些5位或6位的十进制数字。满足如下要求：
该数字的各个数位之和等于输入的整数。
输入格式
一个正整数 n (10< n< 100), 表示要求满足的数位和。
输出格式
若干行，每行包含一个满足要求的5位或6位整数。
数字按从小到大的顺序排列。
如果没有满足条件的，输出：-1
样例输入
44
样例输出
99899
499994
589985
598895
679976
688886
697796
769967
778877
787787
796697
859958
868868
877778
886688
895598
949949
958859
967769
976679
985589
994499

佬の链接
简短判断回文： 如果把最低位放到最高位,秦九昭过程:等效翻转 ==> 若翻转数值相同则为回文串
编写细节：i保持循环顺序不能改变i的值, 需取临时t=i判断条件

举个反例：123：123%10=3 -> 123/10=12 -> 310+12%10=32 -> 12/10=1 ->3210+1%10=321;
则123 != 321 故不是回文数；
求个位数字之和只用在求回文得时候 每次取余得到得数累加求和即可【秦九昭】。

#include 
using namespace std;

int main()
{
    int n; 
	bool flag = false;
    scanf("%d", &n);
    for(int i = 10000; i < 1000000; ++i)
    {
        int t = i, num = 0, sum = 0;//重点：取临时t判断, 不能改变i的值影响遍历 
        while(t)
        {
            num = num * 10 + t % 10;// 简短判断回文： 如果把最低位放到最高位,秦九昭过程:等效翻转 ==> 若翻转数值相同则为回文串   
            sum += t % 10;
            t /= 10;
        }
        if(num == i && sum == n)
        {
            flag = true;
            printf("%d\n", i);
        }
    }
    
    if(!flag) puts("-1");
     
    return 0;
}

第四届

1205. 买不到的数目

时/空限制：1s / 64MB

小明开了一家糖果店。

他别出心裁：把水果糖包成4颗一包和7颗一包的两种。

糖果不能拆包卖。

小朋友来买糖的时候，他就用这两种包装来组合。

当然有些糖果数目是无法组合出来的，比如要买 10 颗糖。

你可以用计算机测试一下，在这种包装情况下，最大不能买到的数量是17。

大于17的任何数字都可以用4和7组合出来。

本题的要求就是在已知两个包装的数量时，求最大不能组合出的数字。

输入格式
两个正整数 n,m，表示每种包装中糖的颗数。

输出格式
一个正整数，表示最大不能买到的糖数。

数据范围
2≤n,m≤1000，
保证数据一定有解。

输入样例：
4 7
输出样例：
17

dfs暴力标记或者小学数论

佬の解答：https://www.acwing.com/solution/content/7101/

算法分析:

引理：给定a，b, 若&d = gcd(a,b) > 1&,则一定不能凑出最大数

结论：

如果 a,b均是正整数且互质，那么由 ax+by, x≥0, y≥0 不能凑出的最大数是 $(a-1)(b-1)-1$

打表找规律方法:（纯摘抄y总的笔记）

#include 

using namespace std;

//给定一个m，是否能用p和q凑出来
bool dfs(int m,int p,int q)
{
    if(m == 0) return true;

    if(m >= p && dfs(m - p,p,q)) return true;
    if(m >= q && dfs(m - q,p,q)) return true;

    return false;
}

int main()
{
    int p,q;
    cin >> p >> q;
    int res = 0;
    for(int i = 1; i <= 1000;i ++)
    {
        if(!dfs(i,p,q)) res = i;
    }

    cout << res << endl;

    return 0;
}

小学数二结论题:

//小学数二结论题(证明略)：若两个整数p、q互质 ，则p,q不能凑出的最小整数为 (p - 1)*(q - 1) - 1;   

#include 

using namespace std;

int n,m;

int main()
{
    cin >> n >> m;
    cout << (n - 1) * (m - 1) - 1 << endl;
    return 0;
}

第十届

Fibonacci 数列与黄金分割

时间限制: 1Sec 内存限制: 128MB
题目描述
Fibonacci 数列是非常著名的数列:

F[1] = 1,

F[2] = 1,

对于 i > 3，F[i] = F[i − 1] + F[i − 2]

Fibonacci 数列有一个特殊的性质，前一项与后一项的比值，F[i]/F[i + 1]， 会趋近于黄金分割。

为了验证这一性质，给定正整数 N，请你计算 F[N]/F[N + 1]，并保留 8 位 小数。

输入格式
一个正整数 N。(1 ≤ N ≤ 2000000000)

输出格式
F[N]/F[N + 1]。答案保留 8 位小数。

样例输入
2
样例输出
0.50000000

枚举范围太大，观察发现20项之后，8位小数精度都一样！！！ 


#include 
using namespace std;
double fib(int n) {
    long long f[n + 1];
    f[1] = 1;
    f[2] = 1;
    for (int i = 3; i <= n; ++i) {
        f[i] = f[i - 1] + f[i - 2];
    }
    return f[n];
}
int main() {
    ios::sync_with_stdio(false);
    //cin.tie(NULL);
    int n;
    cin >> n;   //cout << fixed << setprecision(8) << fib(n) / fib(n + 1) << endl;
    if (n < 20) printf("%.8lf\n",(double)fib(n)/(double)fib(n+1));
 	else cout << "0.61803399" << endl;
   
    return 0;
}

ios::sync_with_stdio(false);这条语句关掉scanf 和cin 的同步加快效率。但是即使是这样cin 还要慢 5倍左右，而且一旦使用了这条语句，scanf和cin 混用可能就会造成一些奇怪的问题。

修改数组

时间限制: 1Sec 内存限制: 128MB 提交: 5491 解决: 1348
题目描述
给定一个长度为 N 的数组 A = [A1, A2, · · · AN ]，数组中有可能有重复出现 的整数。

现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改 A2,A3,··· ,AN。

当修改 Ai 时，小明会检查 Ai 是否在 A1 ∼ Ai−1 中出现过。如果出现过，则 小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过，小明会持续给 Ai 加 1 ，直 到 Ai 没有在 A1 ∼ Ai−1 中出现过。

当 AN 也经过上述修改之后，显然 A 数组中就没有重复的整数了。 现在给定初始的 A 数组，请你计算出最终的 A 数组

输入格式
第一行包含一个整数 N。 第二行包含N个整数A1,A2,··· ,AN

对于 80% 的评测用例，1 ≤ N ≤ 10000。

对于所有评测用例，1 ≤ N ≤ 100000，1 ≤ Ai ≤ 1000000。

输出格式
输出N个整数，依次是最终的A1,A2,··· ,AN。

样例输入
5
2 1 1 3 4
样例输出
2 1 3 4 5

并查集思路：
首先我们每输入一个数，都会判断前面是否已经有过，如果有过就会+1，知道前面没有重复的数。
那么像不像并查集的指向呢，如果没有用过就是自己就是一个集合，根节点指向自己
如果已经用过了，只要将其父节点指向比他大1的节点（此时不重复）就可以。

#include
using namespace std;
const int N = 1000010;
int p[N];
//查找祖宗节点+路径压缩
int find(int x )
{
    if(p[x] != x) p[x] = find(p[x]);
    return p[x];
}
int main()
{
    int n;
    cin>>n;
    for(int i = 0; i < N; i++)
        p[i] = i;
    for(int i = 0; i < n; i++)
    {
        int x;
        scanf("%d",&x);
        x = find(x);
        printf("%d ",x);
        p[x] = x+1;
    }
    return 0;
}

等差数列

时间限制: 1Sec 内存限制: 128MB 提交: 7792 解决: 1804
题目描述
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一 部分的数列，只记得其中 N 个整数。

现在给出这 N 个整数，小明想知道包含这 N 个整数的最短的等差数列有 几项?

输入格式
输入的第一行包含一个整数 N。 第二行包含N个整数A1,A2,···,AN。(注意A1 ∼AN并不一定是按等差数

列中的顺序给出)

(对于所有评测用例，2≤ N ≤100000，0≤ Ai ≤10⁹。)

输出格式
输出一个整数表示答案

样例输入
5
2 6 4 10 20
样例输出
10

题解

乱序先排序，所有相邻两项差的最大公因数， 最大公因数即为 ：最大公差d

#include 
using namespace std;
const int N = 100000;
int a[N];

int gcd(int a,int b) 
{
	if(b == 0)return a;
	return gcd(b,a%b);
}
int main(){
	
    int n;
    scanf("%d",&n);
    
    for(int i=0;i<n;i++){
        scanf("%d",&a[i]);
    }
    sort(a,a+n);
    
    //找最小差值的公约数是公差d;
    int min=a[0],max=a[n-1];
    int d=(a[1]-a[0]);
    for(int i=2;i<n;i++){
        if((a[i+1]-a[i])<=d){//此处d不能换成a[i]-a[i-1]。
            d=gcd(d,a[i]-a[i-1]);//求d与其他差值的公差，赋值
        }
    }
    if(d==0){
        printf("%d",n);
    }else{    
        printf("%d",(max-min)/d+1);
    }
}

十三届

刷题链接整理
蓝桥杯往界真题OJ在线刷题

统计子矩阵

时间限制: 1Sec 内存限制: 256MB 提交: 908 解决: 147
题目描述
给定一个 N × M 的矩阵 A，请你统计有多少个子矩阵 (最小 1 × 1，最大 N × M) 满足子矩阵中所有数的和不超过给定的整数 K?
输入格式
第一行包含三个整数 N, M 和 K.

之后 N 行每行包含 M 个整数，代表矩阵 A.

输出格式
一个整数代表答案。
样例输入
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
样例输出
19
提示
满足条件的子矩阵一共有 19，包含：

大小为 1 × 1 的有 10 个。

大小为 1 × 2 的有 3 个。

大小为 1 × 3 的有 2 个。

大小为 1 × 4 的有 1 个。

大小为 2 × 1 的有 3 个。

对于 30% 的数据，N, M ≤ 20. 对于 70% 的数据，N, M ≤ 100.

对于 100% 的数据，1 ≤ N, M ≤ 500; 0 ≤ Ai j ≤ 1000; 1 ≤ K ≤ 250000000.

如果直接用 前缀和 + 暴力，复杂度将是O(n⁴)，必须优化
优化的方法是：
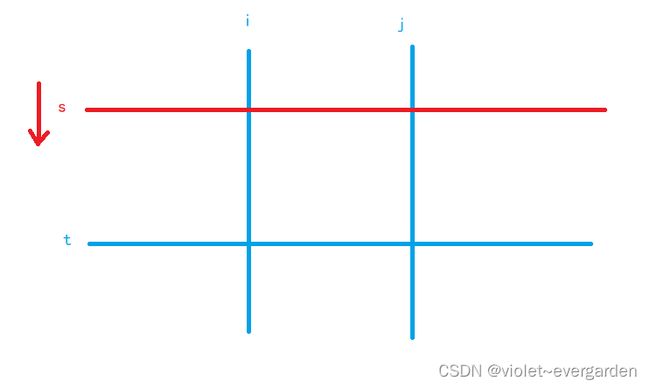
1）枚举子矩阵的 左边界i 和 右边界j，
2）用 快指针t 枚举 子矩阵的下边界，慢指针s 维护 子矩阵的上边界 (s ≤≤ t)
3）如果得到的子矩阵的权值和 大于 k，则慢指针s 前进，而子矩阵和必将单调不增
4）慢指针s 继续前进（如图），直到 子矩阵的和 不大于k，慢指针没必要前进了，因为该子矩阵的所有宽度为 j - i + 1 的子矩阵（总共 t - s + 1 种）一定满足要求，更新该情况对答案的贡献 t - s + 1；反之，如果慢指针s越界（s > t），则不操作，直接进入下层循环

题解

ios::sync_with_stdio(false); 【专用c++の选手】
记 ios::sysn_with_stdio ，没有特殊格式输出就用cin和cout 	
初始化直接存二维前缀和  ： a[i][j] += a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1];

【极简初始前缀和】 ： a[i][j] += a[i - 1][j] 不用原数组，直接覆盖

#include 

using namespace std;

typedef long long LL;

const int N = 510;

int n, m, K;
int s[N][N]; 

int main()
{
    scanf("%d%d%d", &n, &m, &K);

    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
        {
            scanf("%d", &s[i][j]); //边读入边覆盖((不需要用原数组)
            s[i][j] += s[i - 1][j]; //前缀和初始化【极简版】
        }

    LL res = 0;
    for (int i = 1; i <= n; i ++ )//i, j就当做上up与下down边界枚举 
        for (int j = i; j <= n; j ++ )
            for (int l = 1, r = 1, sum = 0; r <= m; r ++ )
            {
                sum += s[j][r] - s[i - 1][r]; 
                while (sum > K) // 超过了：缩小左右边界 : l ++
                {
                    sum -= s[j][l] - s[i - 1][l];  //删去子矩阵的边界L一列,上下边界限制为[i, j]      
                    l ++ ;
                }  //[l-1,r]不满足, [l, r]刚好满足, 则截取[l, r]范围内更小的左右边界的子矩阵均满足 < k
                res += r - l + 1; //长度大小: 1 ~ R-L 均满足 即在[l, r]共有 r - l + 1种长度满足
            }

    printf("%lld\n", res);
    return 0;
}

暴力6重循环(TLE)： 枚举上下左右边界练习

for(int u = 1; u <= m; u++) //up 与 down
    for(int d = u ; d <= m; d++)
        for(int l = 1; l <= n; l++)
            for(int r = l; r <= n; r++)
            { //check(是否子矩阵元素和 >= k)
                子矩阵元素和sum = s[r][d] - s[l - 1][d] -s[r][u - 1] + s[l][u] 左上坐标(l,u)和右下左边(r,d)】
            }

// 接近TLE
// #include    //前缀和+暴力枚举O($n^4$)    
// using namespace std;
// typedef long long LL;
// const int N=510;
// LL a[N][N],s[N][N],cnt,n,m,k;
// inline LL sum(int x1,int y1,int x2,int y2) //内联函数
// {
//     return s[x2][y2]-s[x2][y1-1]-s[x1-1][y2]+s[x1-1][y1-1];
// }
// int main()
// {
//     scanf("%lld%lld%lld",&n,&m,&k);
//     for(int i=1;i<=n;i++)
//     {
//         for(int j=1;j<=m;j++)
//         {
//             scanf("%lld",&a[i][j]);
//             s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];
//         }
//     }
//     for(int l=1;l<=m;l++)//枚举矩阵的左边
//     {
//         for(int r=l;r<=m;r++)//枚举矩阵的右边   【枚举所有[l, r]】
//         {
//             for(int i=1,j=1;i<=n;i++)//从上到下双指针扫描    
//             {
//                 while(j <= i && sum(j,l,i,r) > k) j++;
//                 if(j<=i) cnt+=(i-j+1);//有可能最小的矩阵都不满足，此时j>i
//             }
//         }
//     }
//     printf("%lld",cnt);
//     return 0;
// }

真题乱刷待整理

//蓝桥杯真题解码：简单 
//#include
//#include
//
//using namespace std;
//
//int main() 
//{
//	string s, res;
//	cin >> s;
//	
//	for(int i = 0; i < s.size(); i++)
//	{
//		if( isalpha(s[i]) && isdigit(s[i + 1]) )//字符和单词：此题扩展怎么解呢？ ： 就是连续的字符数量超过9 ： 那么要判断多位数字：要计算数字 
//		{
//			int n = s[i + 1] - '0';
//			for(int j = 0; j < n; j++)
//			{
//				res += s[i];
//			}
//		}
//		else if(isalpha(s[i]) && isalpha(s[i]) )
//		{
//			res += s[i];
//		}
//	}
//	
//	cout << res << endl;
//	
//	return 0;
//}




//根据题目二分前提：升序排列区间
//#include 
//#include 
//#include 
//#include 
//
//using namespace std;
//
//const int N = 100010;
//
//int n, m;
//int q[N];
//
//int main()
//{
//    scanf("%d%d", &n, &m);
//    for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);  //没有&时 ：Segmentation Fault   
//
//    while(m --)
//    {
//    	int x;
//    	scanf("%d", &x);
//    	
//    	int l = 0 , r = n - 1;
//    	while(l < r)
//    	{
//    		int mid = l + r >> 1;
//    		if(q[mid] >= x) r = mid;
//    		else l = mid + 1;
//		}
//		
//		if(q[l] == x)
//		{
//			cout << r << " ";
//			int r = n - 1;
//			while(l < r)
//			{
//				int mid = l + r + 1 >> 1;
//				if(q[mid] <= x) l = mid;
//				else r = mid - 1;
//			}
//			cout << r << endl;
//		}
//		else puts("-1 -1");
//	}
//	
//	
//    return 0;
//}


//答案落的区间 --> 选取两个模板  ： if(check()) 选取模板 

//
//#include
//
//using namespace std;
//
//int main()
//{
//    double x;
//    cin >> x;
//    double l = -10000, r = 10000;//区间范围
//    while (r - l > 1e-8)//误差精度范围 结果所在区间[l,r] < 1e-8    
//    {
//        double mid = (l + r) / 2;//double类型不能位运算 >> 1
//        if (mid * mid * mid <= x) l = mid; //浮点数的二分好处，都是mid
//        else r = mid;
//    }
//
//    printf("%lf\n", l);//double默认6位
//
//    return 0;
//}

//洛谷CSP-J模拟题1 

//洛谷有犇 
//k循环会超时 【暴力过40%】 
#include

using namespace std;

typedef long long LL;

LL x, k;

int main()
{
	scanf("%lld%lld", &x, &k);
	
	while(k--)
	{
		x ++;
		if(x % 3 == 0) x /= 3;
	}
	
	printf("%lld\n", x);
	
	return 0;
}