导向滤波原理浅析
前言
在图像处理上,导向滤波器(Guided Image Filter)是一种能使图像平滑化的非线性滤波器。与双边滤波器(Bilateral Filter)相同,这个滤波器同样能够在清楚保持图像边界的情况下,达到让图像平滑的效果。

但不同于双边滤波器,导向滤波器有两个优点:
- 首先,双边滤波器有非常大的计算复杂度(O(N^2)),但导向滤波器因为并未用到过于复杂的数学计算,有线性的计算复杂度。
- 双边滤波器因为数学模型的缘故,在某些时候会发生梯度反转(gradient reverse)的状况,出现图像有损;而导向滤波器因为在数学上以线性组合为基础出发,输出图片(Output Image)与引导图片(Guidance Image)的梯度方向一致,不会出现梯度反转的问题(大概率不出现,某些条件下必定不出现)。
可以说,导向滤波相比双边滤波的两大优势就是速度快和不会有梯度反转。
实际的应用场景除了去噪平滑外,还可以用于细节加强(detail smoothing/enhancement,如“羽化”)、HDR compression、image matting/feathering、haze removal(去雾)、joint upsampling、深度图修整等功能。

原理
为了达到图像平滑去噪效果,首先定义输出的结果图是输入图减去噪声后的结果。同时,为了让输出图保持引导图的边界,将输出图定为引导图的线性组合。
可以说,导向滤波核心原理是假设导向图I与滤波结果输出图q符合局部(以像素 k k k为中心的 w k w_k wk窗口内)线性模型:
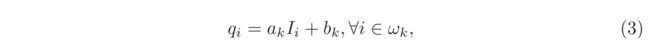
局部线性模型(local linear model)保证了结果图与导向图的edge一致( ∇ q = a ∇ I ∇q = a∇I ∇q=a∇I)。
为了得到线性系数,需要构建方程求解。论文采用的是最小化输出q与输入图p之间的差异,即最小化窗口内的代价函数:

其中 ϵ \epsilon ϵ 是防止 a k a_k ak 过大的正则化参数。
方程的解可以根据 linear regression 求得,细节见参考资料[7]或[18]中推导:
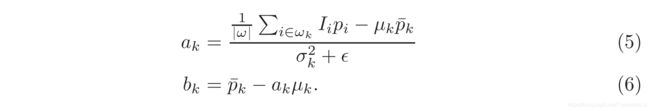
其中, μ k \mu_k μk和 σ k 2 \sigma^2_k σk2是导向图I在窗口 w k w_k wk内的均值和方差, ∣ w ∣ |w| ∣w∣是窗口 w k w_k wk内的像素数目, p ‾ k = 1 ∣ w ∣ ∑ i ∈ w k p i \overline{p}_k=\frac{1}{|w|}\sum_{i\in w_k}{p_i} pk=∣w∣1∑i∈wkpi是窗口 w k w_k wk内的均值。
基本上,根据得到的 a k a_k ak和 b k b_k bk就可以计算得出窗口 w k w_k wk内的每一个 q i q_i qi。但是进一步考虑,由于每一个像素不一定只被一个窗口 w k w_k wk所包含,例如九宫格情况下中心像素点就被9个3x3的 w k w_k wk窗口包含。

所以最简单的方式则是对这9个 w k w_k wk窗口得到的 q i q_i qi做一个加权平均,得到的最终 q i q_i qi才是真正的结果值。

经过对所有 q i q_i qi的加权平均(实际上用的是均值滤波), ∇ q ∇q ∇q不再是 ∇ I ∇I ∇I线性关系。但是由于 ( a ‾ i , b ‾ i ) (\overline a_i, \overline b_i) (ai,bi)是经过均值滤波得到,在导向图的强边界处,输出图的梯度会比导向图小。这种情况下可以认为 ∇ q ≈ a ‾ ∇ I ∇q \approx \overline a∇I ∇q≈a∇I,表示导向图I边界的强变化还能被输出图q维持。

算法伪码如下:

其中, f m e a n ( ⋅ , r ) f_{mean}(·, r) fmean(⋅,r) 是半径为r的均值滤波器。
则可以得到算法伪码中的:
特别说明:
通过参数 ϵ \epsilon ϵ 定义什么是“平坦区块(patch)”或“高变化区块”。若一个区块的方差远低于参数 ϵ \epsilon ϵ ,其通过滤波器后将被平滑;反之,方差远高于 ϵ \epsilon ϵ的区块将被视为边界而被保留。
双边滤波中的范围方差(range variance)参数 σ r 2 \sigma _{r}^{2} σr2的功能和导向滤波的 ϵ \epsilon ϵ相似。它们都定义了什么样的区块应该被平滑,而什么样的区块应该被保留。
实现
核心代码如下:
void GuidedFilterImpl::filter(InputArray src, OutputArray dst, int dDepth /*= -1*/)
{
CV_Assert( !src.empty() && (src.depth() == CV_32F || src.depth() == CV_8U) );
if (src.rows() != h || src.cols() != w)
{
CV_Error(Error::StsBadSize, "Size of filtering image must be equal to size of guide image");
return;
}
if (dDepth == -1) dDepth = src.depth();
int srcCnNum = src.channels();
vector<Mat> srcCn(srcCnNum);
vector<Mat>& srcCnMean = srcCn;
split(src, srcCn);
if (src.depth() != CV_32F)
{
parConvertToWorkType(srcCn, srcCn);
}
vector<vector<Mat> > covSrcGuide(srcCnNum);
computeCovGuideAndSrc(srcCn, srcCnMean, covSrcGuide);
vector<vector<Mat> > alpha(srcCnNum);
for (int si = 0; si < srcCnNum; si++)
{
alpha[si].resize(gCnNum);
for (int gi = 0; gi < gCnNum; gi++)
alpha[si][gi].create(h, w, CV_32FC1);
}
runParBody(ComputeAlpha_ParBody(*this, alpha, covSrcGuide));
covSrcGuide.clear();
vector<Mat>& beta = srcCnMean;
runParBody(ComputeBeta_ParBody(*this, alpha, srcCnMean, beta));
parMeanFilter(beta, beta);
parMeanFilter(alpha, alpha);
runParBody(ApplyTransform_ParBody(*this, alpha, beta));
if (dDepth != CV_32F)
{
for (int i = 0; i < srcCnNum; i++)
beta[i].convertTo(beta[i], dDepth);
}
merge(beta, dst);
}
具体文件参考GitHub的OpenCV Contrib包实现。
GPU版导向滤波实现参考GitHub - TracelessLe/pybind11_guidedfilter_cuda。
cv::cuda::GpuMat GuidedFilterMono::filterSingleChannel(const cv::cuda::GpuMat &p, cv::cuda::Stream &stream) const {
cv::cuda::GpuMat mean_p, mean_Ip, cov_Ip;
box_filter->apply(p, mean_p, stream);
cv::cuda::multiply(I, p, mean_Ip, 1, -1, stream);
box_filter->apply(mean_Ip, mean_Ip, stream);
cv::cuda::multiply(mean_I, mean_p, cov_Ip, 1, -1, stream);
cv::cuda::subtract(mean_Ip,
cov_Ip,
cov_Ip,
cv::noArray(),
-1,
stream); // this is the covariance of (I, p) in each local patch.
cv::cuda::GpuMat a, b;
cv::cuda::add(var_I, cv::Scalar(eps), a, cv::noArray(), -1, stream);
cv::cuda::divide(cov_Ip, a, a, 1, -1, stream); // Eqn. (5) in the paper;
cv::cuda::multiply(a, mean_I, b, 1, -1, stream);
cv::cuda::subtract(mean_p, b, b, cv::noArray(), -1, stream); // Eqn. (6) in the paper;
box_filter->apply(a, a, stream);
box_filter->apply(b, b, stream);
cv::cuda::multiply(a, I, a, 1, -1, stream);
cv::cuda::add(a, b, a, cv::noArray(), -1, stream);
return a;
}
扩展讨论
(1)相比双边滤波,导向滤波有速度快和避免梯度反转等优势。

(2)基于原始的导向滤波算法引入resize得到的Fast导向滤波能够将时间复杂度从O(N)降到O(N / r^2),同时保证滤波结果图像质量损失不大。其中r是resize(或称之为scale)的倍数。

参考资料
[1] wikipedia - Edge-preserving smoothing
[2] 维基百科 - 引导影像滤波器
[3] Guided Image Filtering - Kaiming He
[4] GitHub - opencv_contrib/modules/ximgproc/src/guided_filter.cpp
[5] OpenCV Docs - GuidedFilter
[6] 知乎 - 导向滤波原理(Guided Filter)
[7] 知乎 - 引导滤波guideFilter原理推导与实验
[8] 维基百科 - 方差
[9] 维基百科 - 协方差
[10] 知网 - 引导滤波算法的CUDA加速实现
[11] 豆丁网 - 引导滤波算法的CUDA加速实现
[12] GitHub - acstacey/GLFCV/src/guidedfilter.cpp
[13] GitHub - xxxzhou/oeip/oeip-win-cuda/GuidedFilterLayer.cpp
[14] cnblogs - CUDA加opencv复现导向滤波算法
[15] GitHub - foowaa/3DVisionUnit/GuidedFitlerOptimzation_CUDA/GuidedFilter.cu
[16] GitHub - TracelessLe/pybind11_guidedfilter_cuda
[17] csdn - 双边滤波原理浅析
[18] 导向滤波 Guided Image Filtering



