面试中的深度学习基础问题

Batch Normalization

由于Internal Covariate Shift(Google)效应产生，即深度神经网络随着网络层数的加深，该层的输入会发生变化，使得输入不满足独立同分布的条件，反而向激活函数的两端移动（梯度很小），导致梯度消失，收敛困难。可在每层的激活函数前，加入BN，将参数重新拉回0-1正态分布，加速收敛。理想情况下，Normalize的均值和方差应当是整个数据集的，但为了简化计算，就采用了一个mini-batch内的。

注意图中的最后一步scale and shift。如果不加这一步，那么每层的输入都规范到0均值1方差的正态分布，这样会弱化前边网络层的学习能力，这显然是不太合理的，所以就加了shift（平移）与 scale（缩放）进行平移和缩放。

测试时均值和方差不再用每个mini-batch来替代，而是训练过程中每次都记录下每个batch的均值和方差，训练完成后计算整体均值和方差用于测试。

白化操作，例如PCA，也可以起到规范化分布的作用，但是计算成本过高。

BN对于Relu是否仍然有效？
有效，学习率稍微设置大一些，会使输入有更大的可能落入ReLU函数的负区间(梯度为0)，神经元就会永远无法激活，导致dead relu问题。BN可以将数据分布拉回来。
四种主流规范化方法

多卡同步
BN的多卡同步是，单卡进行计算后，多卡之间通信计算出整体的均值和方差，用于BN计算。
2次同步：先在多卡之间传递均值，再传递方差。

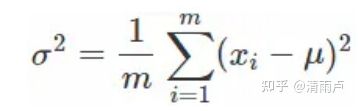
1次同步：一次传递$x$与$x^2$。

逻辑斯蒂回归（LR, Logistic Regression)

Logistic 分布
Logistic 分布是一种连续型的概率分布，其分布函数和密度函数分别为：

其中， $\mu$ 表示位置参数， $\gamma$为形状参数。我们可以看下其图像特征：

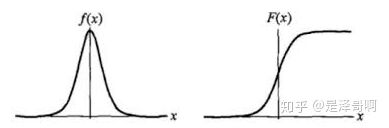
Logistic 分布的形状与正态分布的形状相似，但是 Logistic 分布的尾部更长，所以我们可以使用 Logistic 分布来建模比正态分布具有更长尾部和更高波峰的数据分布。在深度学习中常用到的 Sigmoid 函数就是 Logistic 的分布函数在$\mu =0,\gamma =1$ 的特殊形式。
Logistic 回归
模型：
$$p(x)=\sigma (\sum _{i=1}^m{w}_i{x}_i+b)，m为特征个数$$

损失函数：

求解方法：1.随机梯度下降法 2.牛顿法

考虑二分类任务, 其输出标记 $y\in \{0,1\}$ , 而线性回归模型产生的预测值 $z={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$是实值, 于是, 我们需将实值 z 转换为 0 / 1 值. 最理想的是 “单位阶跃函数” (unit-step function)：

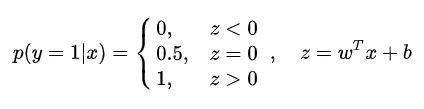
但，单位阶跃函数不可导，则用sigmoid函数替代：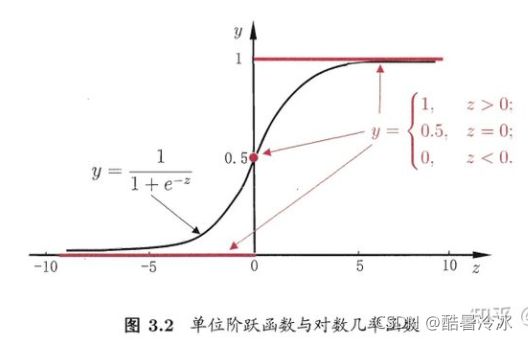

因为阶跃函数不连续，寻找替代函数如 sigmoid:
$$y=\frac{1}{1+e^{-z}}$$
$$y=\frac{1}{1+e^{-\left({\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b\right)}}$$
作变换可得到:
$$\ln \frac{y}{1-y}={\mathbf{w}}^{\mathrm{T}}\mathbf{x}+b$$
即用线性回归的结果去拟合事件发生几率(“几率”是事件发生与不发生的概率比值)的对数，这就是“对数几率回归”的名称来由，其名为回归，实际上是做分类任务。

相关问题
一、LR有什么特点？
简单、容易欠拟合、值域为(0,1)、无穷阶连续可导。
各feature之间不需要满足条件独立假设，但各个feature的贡献独立计算
二、Sigmoid变化的理解？
a) sigmoid函数光滑，处处可导，导数还能用自己表示
b) sigmoid能把数据从负无穷到正无穷压缩到0，1之间，压缩掉了长尾。
c) sigmoid在有观测误差的情况下最优的保证了输入信号的信息。

为什么不用均方误差作为损失？

• 交叉熵的损失函数只和分类正确的预测结果有关系，而MSE的损失函数还和错误的分类有关系
• 交叉熵比均方误差的收敛速度更快

交叉熵与softmax

交叉熵是这样表示的，p(x)为标签，q(x)为预测。
$$H(p,q)=-\sum _{x}p(x)\log q(x)$$
二分类的时候也可以这样表示：

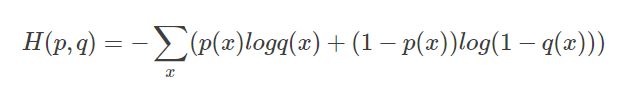
交叉熵不适用于回归问题
当MSE和交叉熵同时应用到多分类场景下时，MSE对于每一个输出的结果都非常看重，而交叉熵只对正确分类的结果看重。

举例：在一个三分类模型中，模型的输出结果为（a,b,c)，而真实的输出结果为(1,0,0)

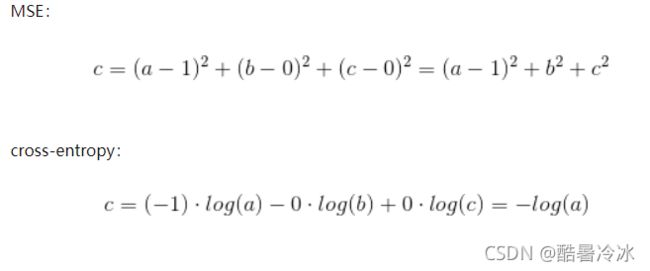
Softmax
$${\sigma }_i(z)=\frac{e^{z_i}}{{\sum }_{j=1}^m{e}^{z_i}}$$

1）为什么要引入指数形式？
如果使用max函数，虽然能完美的进行分类但函数不可微从而无法进行训练，引入以 e 为底的指数并加权归一化，一方面指数函数使得结果将分类概率拉开了距离，另一方面函数可微。
2）为什么不用2、4、10等自然数为底而要以 e 为底呢？
主要是以e为底在求导的时候比较方便。

激活函数的意义

激活函数的主要作用是提供网络的非线性建模能力。

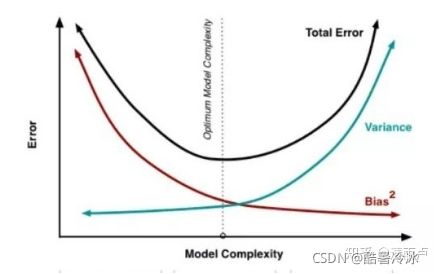
泛化误差（过拟合）

泛化误差 = 方差 + 偏差 + 噪声

1. 噪声是模型训练的上限，也可以说是误差的下限，噪声无法避免。
2. 方差表示不同样本下模型预测的稳定程度（方差大其实就是过拟合，预测不稳定）
3. 偏差表示模型对训练数据的拟合程度 （偏差大就是欠拟合，预测效果不好）

降低方差的方法：（其实就是防止过拟合）
数据：1，增大数据量，进行数据增强
2，进行数据清洗（纠正错误数据）
3，进行特征选择，降低特征维度
4，类别平衡（欠采样、过采样）
网络结构：1，正则化L1,L2, BN 2,dropout
宏观：1，选择合适复杂度的模型，或对已有模型进行剪枝、删减
2，集成学习(Ensemble)
3，限制训练

降低偏差的方法：（防止欠拟合）
输入： 优化特征，检查特征工程是否有漏掉的具有预测意义的特征
网络中间：削弱或者去除已有的正则化约束
宏观：1,增加模型复杂度， 2，集成学习(Ensemble) 3,增大训练轮数

*注：集成学习可以同时降低方差与偏差

逻辑回归（Logistic Regression)

以二分类为例：
$$\text{ 数据: }D={\left(x_i,y_i\right)}_{i=1}^N,y_i=0或1,x_i\in {\mathbb{R}}^p,\sigma (z)=\frac{1}{1+e^{-z}},设\sigma \left(w^{\top }x\right)为1的概率$$

$$\begin{array}{l}P(y=0)\iff P_0=1-\sigma \left(w^{\top }x\right)\\ P(y=1)\iff P_1=\sigma \left(w^{\top }x\right)\end{array}\}p(y\mid x)=p_0^{1-y}{p}_1^y$$
$$\begin{array}{rl}MLE:\hat{w}& =\underset{w}{\mathrm{argmax}}\log \sum _{i=1}^N{P}_0^{1-y_i}{P}_1^{y_i}\\ & =\underset{w}{\mathrm{argmax}}\sum _{i=1}^N\log P_0^{1-y_i}{P}_1^{y_i}\\ & =\underset{w}{\mathrm{argmax}}\underset{-CrossEntropy}{\sum _{i=1}^N(1-y_i)\log (1-\sigma (z_i))+y_i\log \sigma (z_i)},z_i=w^T{x}_i\end{array}$$
可以看出最大似然估计MLE与计算损失Cross Entropy 等价。
$$L(w)=CrossEntropy=\sum _{i=1}^N-y_i\log \sigma (z_i)+(y_i-1)\log [1-\sigma (z)]$$
$$\frac{\partial L}{\partial w}=\frac{\partial L}{\partial \sigma (z)}\cdot \frac{\partial \sigma (z)}{\partial z}\cdot \frac{\partial z}{\partial x}$$
$$\begin{array}{rl}\frac{\partial L}{\partial \sigma }& =\sum _{i=1}^N\frac{-y_i}{\sigma \left(z_i\right)}+\frac{1-y_i}{1-\sigma (z_i)}\\ & =\sum _{i=1}^N\frac{-y_i+y_i\sigma (z_i)+\sigma (z_i)-y_i\sigma (z_i)}{\sigma (z_i)\left[1-{\sigma }_i(z)\right]}\\ & =\sum _{i=1}^N\frac{-y_i+\sigma (z_i)}{\sigma (z_i)\left[1-{\sigma }_i(z_i)\right]}\end{array}$$
而，$\sigma (z)$的导数为：
$$\begin{array}{rl}{\sigma }^{\prime }(z)& =\frac{1}{1+e^{-z}},\\ & =-\frac{1}{{\left(1+e^{-z}\right)}^2}\times \left(e^{-z}\right)\times (-1)\\ & =\frac{e^{-z}}{{1+e^{-z})}^2}=\frac{1+e^{-z}-1}{{\left(1+e^{-z}\right)}^2}=\frac{1}{1+e^{-z}}-\frac{1}{{\left(1+e^{-z}\right)}^2}\\ & =\sigma (z)-{\sigma }^2(z)\\ & =\sigma (z)(1-\sigma (z))\end{array}$$
则$$\begin{array}{rl}\frac{\partial L}{\partial w}& =\frac{\partial L}{\partial \sigma (z)}\cdot \frac{\partial \sigma (z)}{\partial z}\cdot \frac{\partial z}{\partial x}\\ & =\sum _{i=1}^N\frac{-y_i+\sigma (z_i)}{\sigma (z_i)\left[1-{\sigma }_i(z_i)\right]}\cdot \sigma (z_i)(1-\sigma (z_i))\cdot x_i\\ & =\sum _{i=1}^N{x}_i(-y_i+\sigma (z_i))\end{array}$$
参数更新：
$$w^{\prime }=w-\eta \sum _{i=1}^N{x}_i(-y_i+\sigma (z_i)),\eta 为学习率$$

Dropout

前向传播时按概率p随机关闭神经元（每个neuron, 有p%的可能性被去除;（注意不是去除p比例的神经元），本次反向传播时，只更新未关闭的神经元

训练与测试：

训练时开启Dropout，测试时关闭Dropout，否则测试时同一样本多次预测结果会不同。
Dropout使训练和测试时存在差异，为了平衡训练与测试的差异，可以采取使得训练与测试的输出期望值相等的操作：
1，训练时除以p：假设一个神经元的输出激活值为a，在不使用dropout的情况下，其输出期望值为a，如果使用了dropout，神经元就可能有保留和关闭两种状态，把它看作一个离散型随机变量，它就符合概率论中的0-1分布，其输出激活值的期望变为 p*a+(1-p)*0=pa，此时若要保持期望和不使用dropout时一致，就要除以 p。
2, 测试时乘p：测试时关闭了Dropout，此时的期望变成了a/p，因此需要乘以p。

Dropout为什么能减轻过拟合？

1. 模拟了ensemble：训练过程中每次随机关闭不同的神经元，网络结构已经发生了改变，整个dropout的训练过程就相当于很多个不同的网络取平均，进而达到ensemble的效果。
2. 减少神经元之间复杂的共适应关系：dropout导致每两个神经元不一定每一次都在网络中出现，减轻神经元之间的依赖关系。 阻止了某些特征仅仅在其它特定特征下才有效果的情况，从而迫使网络无法关注特殊情况，而只能去学习一些更加鲁棒的特征。

BN和Dropout共同使用出现的问题

Dropout为了平衡训练和测试的差异，会通过随机失活的概率来对神经元进行放缩，进而会改变其方差。如果再加一层BN，又会将方差拉回至（0-1）分布，进而产生方差冲突。
处理方法：1，始终将Dropout放在BN后 2，使用高斯Dropout，使误差变得很小