自己动手写编译器:DFA状态机最小化算法
上一节我们完成了从NFA到DFA的状态机转换,有个问题是状态机并非处于最有状态:
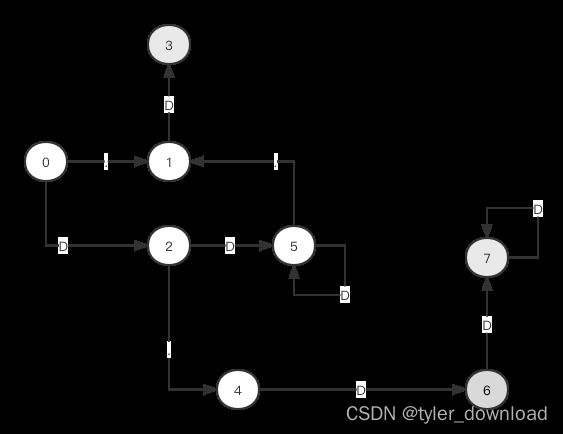
在上图的状态机中,状态6和7其实可以合成一个状态点,本节我们看看如何将这类节点进行合并,使得状态机处于最精简状态(状态4也是终结点,图中有误)。
首先我们把所有节点罗列成下表:
| 所有节点 | 输入字符D后跳转 | 输入字符.后跳转 | 是否是接收状态 |
|---|---|---|---|
| 0 | 2 | 1 | no |
| 1 | 3 | _ | no |
| 2 | 5 | 4 | no |
| 3 | _ | _ | yes |
| 4 | 6 | _ | yes |
| 5 | 5 | 1 | no |
| 6 | 7 | _ | yes |
| 7 | 7 | _ | yes |
第一步我们先把节点根据是否为终结点分成两组,非终结点为一组,终结点为一组,并给每组设置编号,第一组编号0,第二组编号1:
[0,1,2,5]->(0), [3,4,6,7]->(1)
接下来我们分别进入每个分区,分别取出其中两个节点,如果他们接收相同输入,如果跳转的节点在不同分区,那么我们就认为这两个节点不能合成一个点,首先我们看分区0中的点0,它接收D后跳转到2,而节点2位于分区0;分区0中的点1接收D后跳转到节点3,它位于分区1;分区0中节点2接收D后跳转到节点5,后者位于分区0;分区0中节点5接收D后跳转5,后者同样位于分区0,于是我们把分区0中的节点1单独隔离出来形成一个分区:
[0,2,5]->(0), [1]->(2), [3,4,6,7]->(1)
接着我们看分区1,分区1中的节点3接收D后没有跳转,节点4接收D后跳转6,后者位于分区1;节点6,7接收D后跳转分区1,因此节点3要从分区1中隔离出来自己形成一个分区:
[0,2,5]->(0), [1]->(2), [3]->(3), [4,6,7]->(1)
接下来我们以输入’.‘来看每个分区,在分区0中节点0接收’.‘后跳转1,后者位于分区2;节点2接收’.‘,跳转到节点4,后者位于分区1,节点5接收’.'后跳转到节点1,后者为于分区2,因此我们把节点2从分区0中区分开成为一个新分区:
[0,5]->(0), [1]->(2), [3]->(3), [2]->(4), [4,6,7]->(1)
对于只有1个节点的分区我们可以忽略,现在我们看分区1,节点4接收’.‘后没有跳转,节点6接收’.'后没有跳转,节点7接收’.'后也是没有跳转,因此这三个点依然可以属于同一个分区。接下来我们继续返回到分区0,节点0接收D后跳转节点2,后者位于分区4,节点5接收D后跳转到节点5,后者位于分区0,因此我们把点0从分区0拿出来形成一个新分区:
[5]->(0), [1]->(2), [3]->(3), [2]->(4),[4,6,7]->(1), [0]->(5)
由此我们把节点4,6,7合并成一个节点,其他分区都只有一个节点,现在我们用分区编号替代每个分区集合中的点,由此得到DFA状态机如下:
下面我们给出算法的步骤描述,首先给出变量声明:
c: 当前输入字符
group: 一个分区中节点的集合,它也对应一个分区
groups: 当前分区集合
new: 当前分区中被拿出来的节点集合
first: 当前分区中第一个节点
next: 分区中不同于first的另一个节点,如果当前分区除了first对应节点外没有其他未访问过的节点,那么它取值nil
go_first: first对应节点在接收c表示的输入后跳转的节点
go_next: next对应节点接收c表示输入后跳转的节点。
初始化:
先将所有非终结节点放入分区0,将所有终结节点放入分区1,于是groups中包含两个group对象
重复如下步骤,直到groups为空
for(从groups中取出一个group) {
new = []
first = group中第一个节点
next = group中不同于first的节点,如果没有新节点那么设置为nil
for next {
for (当前输入字符c) {
go_first = first 对应节点接收字符c后跳转的节点
go_next = next对应节点接收字符c后跳转的节点
if go_first 和 go_next不属于同一个分区,把next对应节点加入到集合new
}
next 指向当前集合中下一个节点
}
if new != nil {
groups = append(groups, new
}
}
下面我们看看具体代码实现,在nfa_to_dfa.go中继续添加以下代码:
func (n *NfaDfaConverter) initGroups() {
//先把节点根据接收状态分为两个分区
for i := 0; i < n.nstates; i++ {
if n.dstates[i].isAccepted {
n.groups[1] = append(n.groups[1], n.dstates[i].state)
//记录状态点对应的分区
n.inGroups[n.dstates[i].state] = 1
} else {
n.groups[0] = append(n.groups[0], n.dstates[i].state)
n.inGroups[n.dstates[i].state] = 0
}
}
n.numGroups = 2
}
func (n *NfaDfaConverter) printGroups() {
//打印当前分区的信息
for i := 0; i < n.numGroups; i++ {
group := n.groups[i]
fmt.Printf("分区号: %d", i)
fmt.Println("分区节点如下:")
for j := 0; j < len(group); j++ {
fmt.Printf("%d ", group[j])
}
fmt.Printf("\n")
}
}
func (n *NfaDfaConverter) minimizeGroups() {
for {
oldNumGroups := n.numGroups
for current := 0; current < n.numGroups; current++ {
//遍历每个分区,将不属于同一个分区的节点拿出来形成新的分区
if len(n.groups[current]) <= 1 {
//对于只有1个元素的分区不做处理
continue
}
idx := 0
//获取分区第一个元素
first := n.groups[current][idx]
newPartition := false
for idx+1 < len(n.groups[current]) {
next := n.groups[current][idx+1]
//如果分区还有未处理的元素,那么看其是否跟first对应元素属于同一分区
for c := MAX_CHARS - 1; c >= 0; c-- {
gotoFirst := n.dtrans[first][c]
gotoNext := n.dtrans[next][c]
if gotoFirst != gotoNext && (gotoFirst == F || gotoNext == F || n.inGroups[gotoFirst] != n.inGroups[gotoNext]) {
//如果first和next对应的两个节点在接收相同输入后跳转的节点不在同一分区,那么需要将next对应节点加入新分区
//先将next对应节点从当前分区拿走
n.groups[current] = append(n.groups[current][:idx+1], n.groups[current][idx+2:]...)
n.groups[n.numGroups] = append(n.groups[n.numGroups], next)
n.inGroups[next] = n.numGroups
newPartition = true
break
}
}
if !newPartition {
//如果next没有被拿出当前分区,那么idx要增加去指向下一个元素
idx += 1
} else {
//如果next被挪出当前分区,那么idx不用变就能指向下一个元素♀️
newPartition = false
}
}
if len(n.groups[n.numGroups]) > 0 {
//有新的分区生成,因此分区计数要加1
n.numGroups += 1
}
}
if oldNumGroups == n.numGroups {
//如果没有新分区生成,算法结束
break
}
}
n.printGroups()
}
func (n *NfaDfaConverter) fixTran() {
newDTran := make([][]int, DFA_MAX)
//新建一个跳转表
for i := 0; i < n.numGroups; i++ {
newDTran[i] = make([]int, MAX_CHARS)
}
/*
我们把当前分区号对应一个新的DFA节点,当前分区(用A表示)中取出一个节点,根据输入字符c获得其跳转的节点。
然后根据跳转节点获得其所在分区(用B表示),那么我们就得到新节点A在接收字符c后跳转到B节点 。
这里我们从当前分区取出一个节点就行,因为在minimizeGroups中我们已经确保最终的分区中,里面每个节点在接收
同样的字符后,所跳转的节点所在的分区肯定是一样的。
*/
for i := 0; i < n.numGroups; i++ {
//从当前分区取出一个节点即可
state := n.groups[i][0]
for c := MAX_CHARS - 1; c >= 0; c-- {
if n.dtrans[state][c] == F {
newDTran[state][c] = F
} else {
destState := n.dtrans[state][c]
destPartition := n.inGroups[destState]
newDTran[state][c] = destPartition
}
}
}
n.dtrans = newDTran
}
func (n *NfaDfaConverter) MinimizeDFA() {
n.initGroups()
n.minimizeGroups()
n.fixTran()
}
func (n *NfaDfaConverter) PrintMinimizeDFATran() {
for i := 0; i < n.numGroups; i++ {
for j := 0; j < MAX_CHARS; j++ {
if n.dtrans[i][j] != F {
fmt.Printf("from state %d jump to state %d with input: %s\n", i, n.dtrans[i][j], string(j))
}
}
}
}
完成上面代码后,我们在main.go调用一下上面的实现:
func main() {
lexReader, _ := nfa.NewLexReader("input.lex", "output.py")
lexReader.Head()
parser, _ := nfa.NewRegParser(lexReader)
start := parser.Parse()
parser.PrintNFA(start)
//str := "3.14"
//if nfa.NfaMatchString(start, str) {
// fmt.Printf("string %s is accepted by given regular expression\n", str)
//}
nfaConverter := nfa.NewNfaDfaConverter()
nfaConverter.MakeDTran(start)
nfaConverter.PrintDfaTransition()
nfaConverter.MinimizeDFA()
fmt.Println("---------new DFA transition table ----")
nfaConverter.PrintMinimizeDFATran()
}
上面代码运行后输出结果如下:
分区号: 0分区节点如下:
0
分区号: 1分区节点如下:
3
分区号: 2分区节点如下:
1
分区号: 3分区节点如下:
4 6 7
分区号: 4分区节点如下:
2
分区号: 5分区节点如下:
5
---------new DFA transition table ----
from state 0 jump to state 2 with input: .
from state 0 jump to state 4 with input: 0
from state 0 jump to state 4 with input: 1
from state 0 jump to state 4 with input: 2
from state 0 jump to state 4 with input: 3
from state 0 jump to state 4 with input: 4
from state 0 jump to state 4 with input: 5
from state 0 jump to state 4 with input: 6
from state 0 jump to state 4 with input: 7
from state 0 jump to state 4 with input: 8
from state 0 jump to state 4 with input: 9
from state 1 jump to state 1 with input: 0
from state 1 jump to state 1 with input: 1
from state 1 jump to state 1 with input: 2
from state 1 jump to state 1 with input: 3
from state 1 jump to state 1 with input: 4
from state 1 jump to state 1 with input: 5
from state 1 jump to state 1 with input: 6
from state 1 jump to state 1 with input: 7
from state 1 jump to state 1 with input: 8
from state 1 jump to state 1 with input: 9
from state 2 jump to state 3 with input: .
from state 2 jump to state 5 with input: 0
from state 2 jump to state 5 with input: 1
from state 2 jump to state 5 with input: 2
from state 2 jump to state 5 with input: 3
from state 2 jump to state 5 with input: 4
from state 2 jump to state 5 with input: 5
from state 2 jump to state 5 with input: 6
from state 2 jump to state 5 with input: 7
from state 2 jump to state 5 with input: 8
from state 2 jump to state 5 with input: 9
from state 4 jump to state 3 with input: 0
from state 4 jump to state 3 with input: 1
from state 4 jump to state 3 with input: 2
from state 4 jump to state 3 with input: 3
from state 4 jump to state 3 with input: 4
from state 4 jump to state 3 with input: 5
from state 4 jump to state 3 with input: 6
from state 4 jump to state 3 with input: 7
from state 4 jump to state 3 with input: 8
from state 4 jump to state 3 with input: 9
from state 5 jump to state 2 with input: .
from state 5 jump to state 5 with input: 0
from state 5 jump to state 5 with input: 1
from state 5 jump to state 5 with input: 2
from state 5 jump to state 5 with input: 3
from state 5 jump to state 5 with input: 4
from state 5 jump to state 5 with input: 5
from state 5 jump to state 5 with input: 6
from state 5 jump to state 5 with input: 7
from state 5 jump to state 5 with input: 8
from state 5 jump to state 5 with input: 9
上面输出的跳转表画出来时可能跟我们上面不太一样,不一样的主要是节点的编号,但是节点的跳转结构跟我们在前面的分析完全相符,更详细的讲解和调试演示,请在B站搜索coding迪斯尼。
