【Leetcode-NO.00003】动态规划-Leetcode write up by arttnba3
github pages blog addr
文章目录
- [github pages blog addr](https://archive.next.arttnba3.cn/2020/09/06/%E3%80%90OJ-0x0003-Leetcode%E3%80%91%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E9%83%A8%E5%88%86write-up-by-arttnba3/)
- 0x00.绪论
-
- pre.什么是动态规划算法?
- 0x01.难度:简单
-
- 0x00.[爬楼梯](https://leetcode-cn.com/problems/climbing-stairs/)
-
- 问题分析
-
- 状态转移方程
- 时间复杂度
- 空间复杂度
- 解决方案
-
- C语言版:
- Python语言版:
- 0x01.[面试题 08.01. 三步问题](https://leetcode-cn.com/problems/three-steps-problem-lcci/)
-
- 问题分析
-
- 状态转移方程
- 时间复杂度
- 空间复杂度
- 解决方案
-
- C语言版:
- Python语言版
- 0x02.难度:中等
-
- 0x00.[最长上升子序列](https://leetcode-cn.com/problems/longest-increasing-subsequence/)
-
- 问题分析
- 算法过程
-
- 状态转移方程
- 具体架构
- 时间复杂度
- 空间复杂度
- 进阶:贪心+二分查找
- 0x03.难度:困难
-
- 0x00.[ 监控二叉树](https://leetcode-cn.com/problems/binary-tree-cameras/)
-
- 解法:递归 + 深度优先搜索(DFS) + 动态规划(DP)
-
- 状态转移方程
- 时间复杂度:
- 空间复杂度:
0x00.绪论
动态规划(Dynamic Programming)是一种通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。同时也是各类信息学竞赛( Olympiad in Informatics )中较为常用的算法之一。
作为前·蒟蒻·OIer,对动态规划也是稍微了解一点点的XD,所以现在来简单刷一刷leetcode上动态规划的题Or2
最后更新日期2020.9.7
pre.什么是动态规划算法?
简单而言:
动态规划便是通过寻找出一个问题的重叠子问题/最优子结构来优化对问题的求解,将问题进行分阶段求解,并确保当前阶段是过于所有阶段的完美总结。
具体的可以看看我之前写的博文
0x01.难度:简单
0x00.爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/climbing-stairs
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
问题分析
简单分析:
-
上0级楼梯:有0种走法
-
上1级楼梯:有1种走法:直接跨一阶楼梯
-
上2级楼梯:有2种走法:①先跨一阶再跨一阶;②直接跨两阶楼梯
-
…
-
上N阶楼梯:①先走到第N-1阶,再跨一阶楼梯②先走到N-2阶,再一步跨两阶楼梯:一共是F(N-1)+F(N-2)种走法
也就是说,我们走n级楼梯的走法数量都可以化为①先走到第N-1阶,再跨一阶楼梯②先走到N-2阶,再一步跨两阶楼梯的走法
状态转移方程
F(N) = F(N-1) + F(N-2)
有了这个方程之后,我们只需要知道走1级楼梯的走法数量与走2级楼梯的走法数量,就可以顺利地推出走任意一级楼梯的走法数量
时间复杂度
需要求解n次,故时间复杂度为线性时间复杂度O(N)
空间复杂度
因为我们只需要使用三个变量迭代求解,故空间复杂度为O(1)
解决方案
C语言版:
int climbStairs(int n)
{
if(n == 0)
return 0;
if(n == 1)
return 1;
if(n == 2)
return 2;
int a = 1, b = 2, temp;
for(int i=2;i<n;i++)
{
temp = a;
a = b;
b += temp;
}
return b;
}
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-T2pcaZSt-1605852285729)(https://i.loli.net/2020/09/22/7bw2LteuRUhadgl.png)]
Python语言版:
class Solution:
def climbStairs(self, n: int) -> int:
if n < 3:
return n
a, b = 1, 2
for i in range(2,n):
a,b = b, a+b
return b
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jSHCLBW0-1605852285734)(https://i.loli.net/2020/09/22/NtQO4EmZ7uxWTaf.png)]
肉眼可见的Python效率低下
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lIc1lgTW-1605852285738)(https://i.loli.net/2020/09/22/ZJeAi9vElOyTp7M.png)]
还好这次C不用像洛谷那样手撕大数加减(毕竟不是OI标准23333
0x01.面试题 08.01. 三步问题
三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。
示例1:
输入:n = 3
输出:4
说明: 有四种走法
示例2:输入:n = 5
输出:13
提示:n范围在[1, 1000000]之间
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/three-steps-problem-lcci
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
爬楼梯问题的升级版,总体思路还是一样的:
问题分析
简单分析:
- 上0级楼梯:有0种走法
- 上1级楼梯:有1种走法:直接跨一阶楼梯
- 上2级楼梯:有2种走法:①先跨一阶再跨一阶;②直接跨两阶楼梯
- 上3级楼梯:有4种走法:①先跨一阶再跨一阶再跨一阶;②先跨一阶再跨两阶;③先跨两阶再跨一阶;④直接跨3阶
- …
- 上N阶楼梯:①先走到第N-1阶,再跨一阶楼梯②先走到N-2阶,再一步跨两阶楼梯③先走到N-3阶,再一步跨三阶楼梯:一共是F(N-1)+F(N-2)+F(N-3)种走法
也就是说,我们走n级楼梯的走法数量都可以化为①先走到第N-1阶,再跨一阶楼梯②先走到N-2阶,再一步跨两阶楼梯③先走到N-3阶,再一步跨三阶楼梯的走法
状态转移方程
F(N) = F(N-1) + F(N-2) + F(N-3)
有了这个方程之后,我们只需要知道走1级楼梯的走法数量与走2级楼梯的走法数量,就可以顺利地推出走任意一级楼梯的走法数量
时间复杂度
需要求解n次,故时间复杂度为线性时间复杂度O(N)
空间复杂度
因为我们只需要使用三个变量迭代求解,故空间复杂度为O(1)
解决方案
C语言版:
int waysToStep(int n)
{
if(n < 3)
return n;
unsigned long long int a = 1, b = 1, c = 2, d;
for(int i = 2; i < n ; i++)
{
d = (a+b+c) % 1000000007;
a = b;
b = c;
c = d;
}
return d;
}
Python语言版
class Solution:
def waysToStep(self, n: int) -> int:
if n < 3:
return n
a, b, c = 1, 1, 2
for i in range(2,n):
a,b,c = b, c, (a + b + c)%1000000007
return c
效率上的极巨差距
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ucMSmiJX-1605852285745)(https://i.loli.net/2020/09/22/EMwRvZBWJNSep87.png)]
0x02.难度:中等
0x00.最长上升子序列
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/longest-increasing-subsequence
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
问题分析
最长上升子序列问题可以说是动态规划算法最经典的一个入门问题了,无论是在各大算法书上还是竞赛书上在讲到动态规划时往往会选择使用这个问题来入门
首先我们要求解最长上升子序列,我们就必须要将该序列上的各个结点“串起来”——对于任一结点都使用一个变量来储存在该结点上的最长上升子序列中该结点的下一结点的索引
其次,我们不难发现,对于任一结点与其往前所有结点构成的序列,要求解该序列中的最长上升子序列,我们只需要求解该最长上升子序列中的倒数第二个结点与往前所有结点所构成的序列、再接上该序列的最后一个结点即可
算法过程
状态转移方程
对于任一数字序列a1,a2,…,an,其最长上升子序列的长度为:f(an) = f(am)+1
-
其中am<=an
-
f(am)为数字序列a1,a2,…,an-1所能构成的最大元素amax不大于an的上升子序列中的最大长度
那么我们便可以使用遍历的方法逐一求出序列a1,a1、a2,a1、a2、a3,…,a1、a2、a3、…、an中的最长上升子序列的长度
具体架构
状态转移方程构造出来后,接下来的代码就很好写了。
我们选择采用一个三维数组来储存结点信息
- 第一维:结点的值
- 第二维:结点上的最长上升子序列的长度
- 第三维:结点上的最长上升子序列中该结点的下一结点的索引
我们采用两层循环来对各个结点进行遍历:
- 第一层循环遍历每一个结点
- 第二层循环遍历初始节点到第一层循环结点的前一结点求解到该结点的最长上升子序列
时间复杂度
两层循环嵌套,我们很容易得出时间复杂度为O(N^2)
空间复杂度
使用动态数组的话就是线性空间复杂度O(N)
构造代码如下:
int lengthOfLIS(int* nums, int numsSize)
{
if(numsSize == 0)
return 0;
int n, lis[10000][3]={0},_max = -1;
n = numsSize;
for(int i=0;ilis[j][0])
{
//lis[i][1] = lis[i][1]>lis[j][1]+1?lis[i][1]:lis[j][1]+1,lis[i][2] = j;
//it's too hard to understand, so I chose the following one to get it clear
if(lis[i][1]<=lis[j][1]+1)
{
lis[i][1] = lis[j][1]+1;
lis[i][2] = j;
}
}
}
}
for(int i=0;i_max?lis[i][1]:_max;
}
return _max;
}
由于时间复杂度为O(N^2),成绩不是那么的理想
那么我们能不能再加快一点呢?
进阶:贪心+二分查找
我们可以选择使用贪心算法配合二分查找来解决这个问题(当然这个时候就已经不再是动态规划了,(但是是不是动态规划已经无所谓了!(不
咕了,后面有时间再写
0x03.难度:困难
0x00. 监控二叉树
给定一个二叉树,我们在树的节点上安装摄像头。
节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。
计算监控树的所有节点所需的最小摄像头数量。
示例 1:
输入:[0,0,null,0,0]
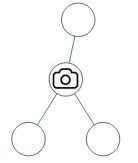
输出:1
解释:如图所示,一台摄像头足以监控所有节点。
示例 2:输入:[0,0,null,0,null,0,null,null,0]
输出:2
解释:需要至少两个摄像头来监视树的所有节点。 上图显示了摄像头放置的有效位置之一。提示:
给定树的节点数的范围是 [1, 1000]。
每个节点的值都是 0。来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/binary-tree-cameras
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
该题为2020.9.22的每日一题
仔细想想,对于一个结点是否需要安装摄像头,其实是由其子树的状态来决定的,那么我们可以使用动态规划算法
解法:递归 + 深度优先搜索(DFS) + 动态规划(DP)
大概如下图所示:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lk9rTQTR-1605852285750)(https://i.loli.net/2020/09/22/5v4sz9fdl2OLau7.png)]
我们考虑有以下几种情况:
- 当一个结点的左或右子树没有被摄像头覆盖上时,这个结点必须要安装一个摄像头来监测其左或右子树,定义为状态码STATUS_CAMERA
- 当一个结点的左右子树都已经被摄像头覆盖上时,为了实现摄像头数量的最小化,需要在该结点的父结点放置摄像头,即在回到父结点前该结点都是未被覆盖的,定义为状态码STATUS_UNCOVERED
- 当一个结点的左右子树中存在摄像头,则该结点肯定是被覆盖了的,定义为状态码STATUS_COVERED
- 对于结点为NULL的情况,我们可以默认他是被覆盖了的结点,即定义为状态码STATUS_COVERED
同时,我们还需要对这棵树的根节点做一次单独的检测,以确定是否要在其上放置摄像头
为了方便判定,我们将STATUS_CAMERA设置为状态码中值相对大的一个
状态转移方程
STATUS_ROOT = F(STATUS_LEFT, STATUS_RIGHT)
时间复杂度:
n次遍历,线性时间复杂度O(N)
空间复杂度:
递归算法要开辟n个栈空间,故为线性空间复杂度O(N)
构造代码如下:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* struct TreeNode *left;
* struct TreeNode *right;
* };
*/
/*
* status code
* 0: waiting for pwn
* 1: has been pwn
* 2: camara here
*-1: inner error, just a placeholder in fact
*/
#define STATUS_UNCOVERED 0
#define STATUS_COVERED 1
#define STATUS_CAMERA 2
#define STATUS_ERROR -1
int minCameraCover(struct TreeNode* root)
{
int amounts=0;//amounts of camera
//add a camera to the root if status of root is 0
if(dfs(root,&amounts) == STATUS_UNCOVERED)
amounts++;
return amounts;
}
int dfs(struct TreeNode* root, int * amounts)
{
//NULL pointer signed as status 1
if(!root)
return STATUS_COVERED;
//get the status of left and right node
int left = dfs(root->left, amounts);
int right = dfs(root->right, amounts);
//if one of both uncovered yet, a camera is needed
if(left == STATUS_UNCOVERED || right == STATUS_UNCOVERED)
{
(*amounts)++;
return STATUS_CAMERA;
}
//if both are covered, father's of root may need a camera
if(left == STATUS_COVERED && right == STATUS_COVERED)
return STATUS_UNCOVERED;
//if there's at least one camera in both childs, the root is covered
if(left + right > STATUS_CAMERA)
return STATUS_COVERED;
//error code(not used)
return STATUS_ERROR;
}
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jcLKxdKo-1605852285751)(https://i.loli.net/2020/09/22/64ytrK3gLNGowbf.png)]