聚类效果的外部评价指标——纯度(Purity)及其Python和matlab实现
0. 前言
我的课题中有一部分是评价聚类结果的好坏,很多论文中用正确率来评价。对此,我一直持怀疑态度,因为在相关书籍中并没有找到“正确率”这一说法,只有分类的时候才用到。若要评价分类结果,Python中直接调用sklearn库中的accuracy_score就可以得出准确率。
那么聚类的“正确率”如何定义又如何计算呢?假设有5个有标签的目标,对应标签表示为y_true=[0,0,0,1,1],根据聚类算法的输出是y_pre=[1,1,1,,0,0],此时聚类结果是完全正确的,因为算法把前三者归为一类,后两者归为一类,只不过表述的不同。若聚类算法的输出是y_pre=[1,1,1,,0,-1],显然该算法将最后一个目标划分错误,此时的“准确率”=0.8 。
1. 纯度(Purity)
后面仔细查询相关文献后,发现聚类效果有一个评价指标——纯度(Purity)。
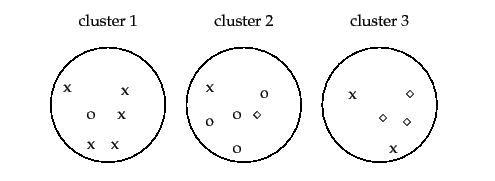
这里引用文献中的例子来说明,假设聚类算法的聚类结果如下图所示,可以看出,聚类算法把样本划分为3个簇:cluster1,2,3。cluster1中x最多,把cluster1看作是x的簇。cluster2中o最多,就看做是o的簇。cluster2中◇最多,就看做是◇的簇。而cluster1中有5个x,cluster2中有4个o,cluster3中有3个◇,总样本数是17个。
那么,此次聚类结果的纯度 P u r i t y = 5 + 4 + 3 17 = 0.71 Purity=\frac{5+4+3}{17}=0.71 Purity=175+4+3=0.71。
现给出纯度的计算公式:
P u r i t y = ∑ i = 1 k m i m p i Purity=\sum_{i=1}^{k}{\frac{m_i}{m}{p_i}} Purity=i=1∑kmmipi
可以发现,纯度就是前言中我一直寻找的所谓“准确率”。
2. 纯度的Python实现
这里主要摘自:https://cloud.tencent.com/developer/ask/189986
from sklearn.metrics import accuracy_score
import numpy as np
def purity_score(y_true, y_pred):
"""Purity score
Args:
y_true(np.ndarray): n*1 matrix Ground truth labels
y_pred(np.ndarray): n*1 matrix Predicted clusters
Returns:
float: Purity score
"""
# matrix which will hold the majority-voted labels
y_voted_labels = np.zeros(y_true.shape)
# Ordering labels
## Labels might be missing e.g with set like 0,2 where 1 is missing
## First find the unique labels, then map the labels to an ordered set
## 0,2 should become 0,1
labels = np.unique(y_true)
ordered_labels = np.arange(labels.shape[0])
for k in range(labels.shape[0]):
y_true[y_true==labels[k]] = ordered_labels[k]
# Update unique labels
labels = np.unique(y_true)
# We set the number of bins to be n_classes+2 so that
# we count the actual occurence of classes between two consecutive bins
# the bigger being excluded [bin_i, bin_i+1[
bins = np.concatenate((labels, [np.max(labels)+1]), axis=0)
for cluster in np.unique(y_pred):
hist, _ = np.histogram(y_true[y_pred==cluster], bins=bins)
# Find the most present label in the cluster
winner = np.argmax(hist)
y_voted_labels[y_pred==cluster] = winner
return accuracy_score(y_true, y_voted_labels)
- 注: 函数
purity_score()的输入y_true和y_pred都得是numpy格式
测试代码:
y_true = np.array([0, 0, 0, 1, 1, 1, 2])
y_pre = np.array([1, 1, 1, 2, 2, 2, 2])
print("纯度为:",purity_score(y_true,y_pre))
- 测试结果:
真的是太好了!!!
3. matlab代码
这里摘自博客
function [FMeasure,Accuracy] = Fmeasure(P,C)
% P为人工标记簇
% C为聚类算法计算结果
N = length(C);% 样本总数
p = unique(P);
c = unique(C);
P_size = length(p);% 人工标记的簇的个数
C_size = length(c);% 算法计算的簇的个数
% Pid,Rid:非零数据:第i行非零数据代表的样本属于第i个簇
Pid = double(ones(P_size,1)*P == p'*ones(1,N) );
Cid = double(ones(C_size,1)*C == c'*ones(1,N) );
CP = Cid*Pid';%P和C的交集,C*P
Pj = sum(CP,1);% 行向量,P在C各个簇中的个数
Ci = sum(CP,2);% 列向量,C在P各个簇中的个数
precision = CP./( Ci*ones(1,P_size) );
recall = CP./( ones(C_size,1)*Pj );
F = 2*precision.*recall./(precision+recall);
% 得到一个总的F值
FMeasure = sum( (Pj./sum(Pj)).*max(F) );
Accuracy = sum(max(CP,[],2))/N;
end
4.更多的评价指标
关于更多的聚类的外部评价指标参考博客
