leetcode1184. 公交站间的距离

---

---

题目

环形公交路线上有 n 个站，
按次序从 0 到 n - 1 进行编号。
我们已知每一对相邻公交站之间的距离，
distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。
环线上的公交车都可以按顺时针和逆时针的方向行驶。
返回乘客从出发点 start 到目的地 destination 之间的最短距离。
来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/distance-between-bus-stops

• 示例1:

输入：distance = [1,2,3,4], start = 0, destination = 1
输出：1
解释：公交站 0 和 1 之间的距离是 1 或 9，最小值是 1。

• 示例2:
  

输入：distance = [1,2,3,4], start = 0, destination = 2
输出：3
解释：公交站 0 和 2 之间的距离是 3 或 7，最小值是 3。

• 示例3:
  

输入：distance = [1,2,3,4], start = 0, destination = 3
输出：4
解释：公交站 0 和 3 之间的距离是 6 或 4，最小值是 4。

---

分析

1. 最短路径

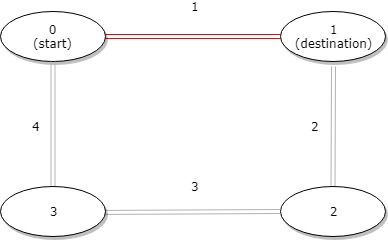
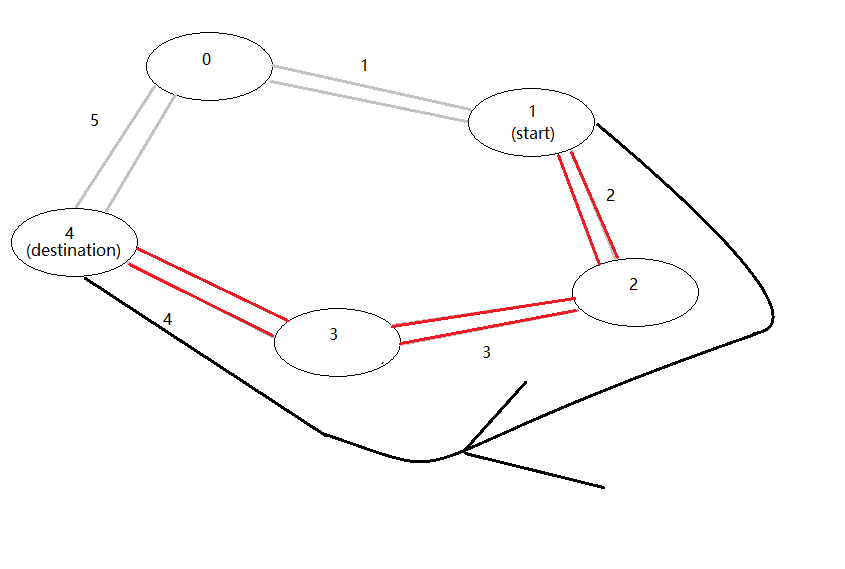
如图:公交车从start站点到destionation站点有两条路径
第一条: 直接走 1
第二条: 先走 4 再走 3 再走 2
最短路径为第一条路径长度为 1, 而第二条路径的长度为 9

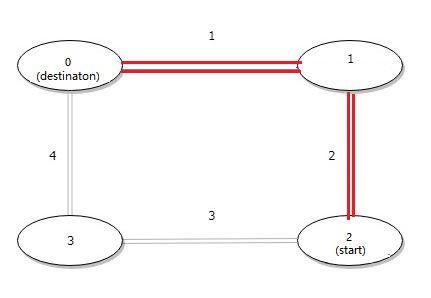
2. 从站点编号大的站点到站点编号小的站点

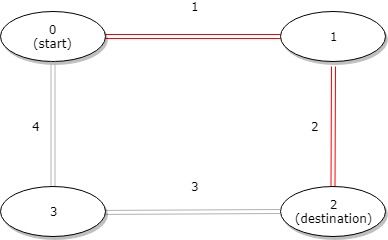
如图:公交车从start站点到destionation站点有两条路径
第一条: 先走 2 再走 1
第二条: 先走 3 再走 4
最短路径为第一条路径，长度为3。 而第二条路径的长度为7。

• 其实从站点2到站点0和从站点0到站点2的情况是一样的

• 如图
  

• 他们的最短路径都是3, 最长路径都是7

所以我们可以把两种情况考虑成一种，当题目给出的start大于destination时，
把start和destination交换一下

---

思路

1. 判断start是否大于destination？如果是, 就交换start和distination的值。

2. 先计算从起始点到终点的一条路径的距离

3. 用总的距离减去前面算出的一条路径距离，就是另外一条路径距离

4. 比较两条路径距离的大小

5. 返回较小的那一条路径

---

突破点

• 怎么计算起点到终点的一条路径的距离?

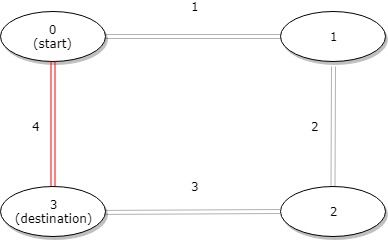
题目的条件: distance = [1,2,3,4], start = 0, destination = 2

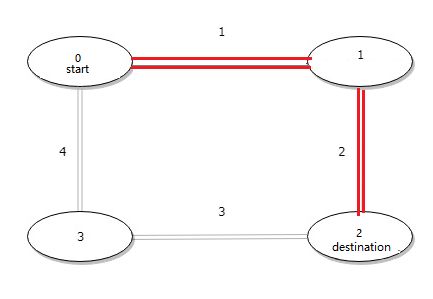
如图，从站点0到站点 2 ，我们不妨先走 1 再走 2 ,也就是顺时针走

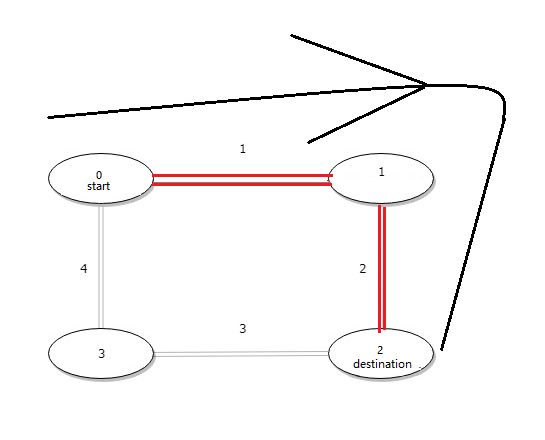
根据题目，
distance[i] 表示编号为 i 的车站和编号为 (i + 1) % n 的车站之间的距离。

站点 0 到站点 1 的距离: distance[0]
站点 1 到站点 2 的距离: distance[1]
所以这条路径的距离为: distance[0] + distance[1]

• 其他情况

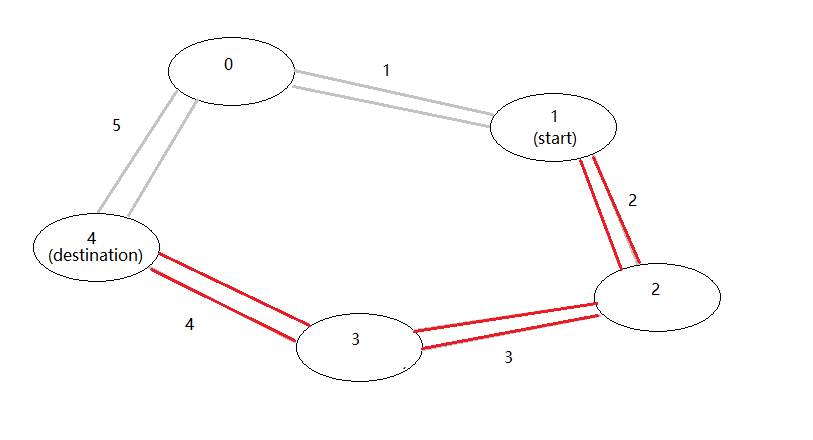
来看下面这个例子:

这里有五个车站，公交车从站点1出发到站点4
条件 ：distance = [1,2,3,4,5], start = 1, destination = 4

我们不妨先顺时针走:

站点 1 到站点 2 的距离: distance[1]
站点 2 到站点 3 的距离: distance[2]
站点 3 到站点 4 的距离: distance[3]
所以这条路径的距离为: distance[1] + distance[2] + distance[3]

• 总结规律我们可以利用循环来计算一条路径
• 大致的代码为:

int distance1 = 0;
for(int i = start; i < destination; i++){
	distance1 += distance[i];
}

---

代码

class Solution {
    public int distanceBetweenBusStops(int[] distance, int start, int destination) {
        //第一条路径
        int distance1 = 0;
        //第二条路径
        int distance2 = 0;
        //总的距离
        int sum = 0;
        //1.判断start是否大于destination
        if(start > destination){
            int temp = start;
            start = destination;
            destination = temp;
        }
        //2.计算从起点到终点的第一条路径
        for(int i = start; i < destination; i++){
            distance1 += distance[i];
        }
        //3.计算总的距离
        for(int j = 0; j < distance.length; j++){
            sum += distance[j];
        }
        //4.计算第二条路径的大小
        distance2 = sum - distance1; 
        //5. 返回较小者
        return distance1 > distance2 ? distance2 : distance1;
    }
}

---

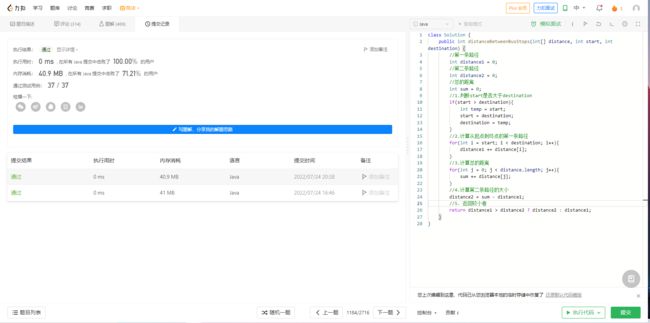
执行结果

可以看到全部的示例都通过了:

如果有其他的思路，可以再评论区发挥你的聪明才智