逻辑回归(吴恩达机器学习笔记)

1.分类问题

 在分类问题中，要预测的变量y是一个离散的值，尝试预测的结果是否属于某一个类，如：判断一封电子邮件是否是垃圾邮箱，区分一个肿瘤是恶性的还是良性的。
 我们将因变量可能属于的两个类分别称为负向类和正向类，则因变量y∈0，1，其中0表示负向类，1表示正向类。

2.假说表示

 ，在逻辑回归中我们引入一个新的模型，该模型的输出变量范围始终在0和1之间。逻辑回归的假设是：$h_{\theta }(x)=g({\theta }^{T}X)$,其中x代表特征向量，g代表逻辑函数（常用的一个逻辑函数为s型函数（Sigmoid function）），公式为:$g(z)=\frac{1}{1+e^{-z}}$.该函数图形为：
 $h_{\theta }(x)$表示根据选择的参数模型计算出输出值为1的概率，即$h_{\theta }(x)=P(y=1|x;\theta )$

3.判定边界

 在逻辑回归中，我们预测：
当$h_{\theta }(x)>=0.5$时，预测y=1.
当$h_{\theta }(x)<0.5$时，预测y=0.
根据S型函数的图像可知：
z=0,g(z)=0.5;
当z>0,g(z)>0.5,
当z<0,g(z)<0.5;
由于z=${\theta }^{T}X$,所以当${\theta }^{T}X>=0$时，y=1，当${\theta }^{T}X<0$时，y=0；
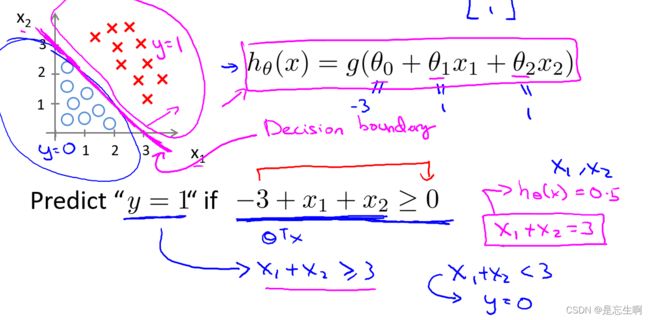
假设有一个模型：$h_{\theta }(x)=g({\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2)$,我们假设${\theta }_0=-3$，则$h_{\theta }(x)>0.5,只需$x_{1}+x_{2}>3$。则在图中画出该线，这条线便是我们的模型的分界线，称为判断边界。

4.代价函数

 在线性回归中，使用了均方误差作为代价函数，理论来说可以在此处也使用该模型。但是由于$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$,该函数不是一个凸函数，则会有许多局部最小值，会影响梯度下降法寻找全局最小值。

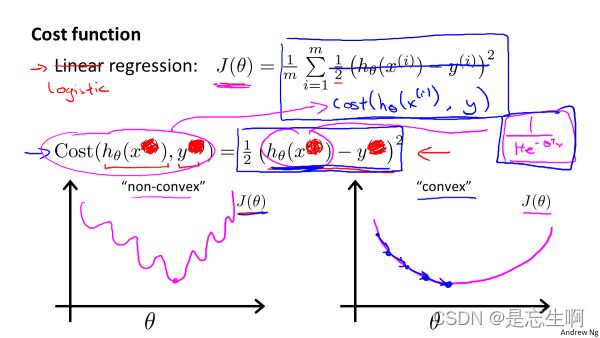
 所以我们重新定义逻辑回归的代价函数：
$J(\theta )=\frac{1}{m}{\sum }_{i=1}^m\frac{1}{2}Cost(h_{\theta }(x^{(i)}),y^{(i)})$其中：

$h_{\theta (x)}$与Cost$(h_{\theta (x)},y)$之间的函数关系为：

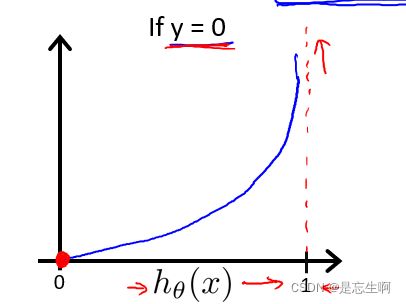
由于y为离散型变量，故Cost可化简为：

将其带入到代价函数中得：

5.应用梯度下降法

 在找出代价函数后，需要找出$J(\theta )$的最小值，此时的参数$\theta$就是要拟合出的合适的参数。于是我们可以使用梯度下降法来最小化代价函数。
 首先对代价函数求偏导：
$\frac{\partial }{\partial J(\theta )}=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})x_j^{(i)}$
 运用梯度下降法，同时更新各参数$\theta$的值：
${\theta }_j={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)})x_j^{(i)}$
$$\theta =\left[\begin{array}{c}{\theta }_0\\ {\theta }_1\\ ...\\ {\theta }_n\end{array}\right]$$

6.多类别分类：一对多

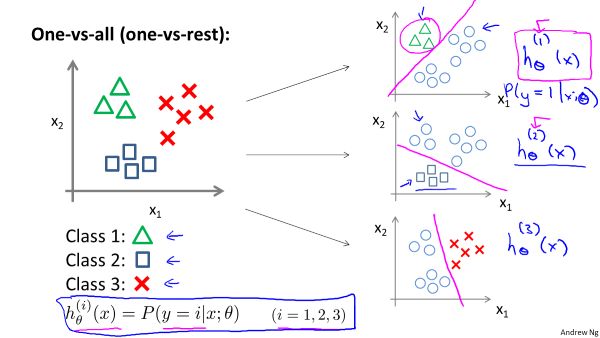
 3 种不同的符号来代表 3 个类别,对于多个类别分类问题，可以将其转换为二分类问题。首先从三角形的类别开始，可以创建一个新的为训练集，将类别2和类别3定位负向类，类别1定义为正向类，则可以拟合出一个合适的模型。对于类别2和类别3同样如此操作，则最终可以得到三个分类模型。对于同一个输入，其输出结果就是三种模型中概率值最高的那个。