1. 摘要
本篇博客简单介绍下用隐马尔科夫模型(Hidden Markov Model, HMM)来解决地图匹配(Map-Matching)问题。转载请注明网址。
2. Map-Matching(MM)问题
根据wikipedia的定义,地图匹配是将一系列有序的用户或者交通工具的位置关联到电子地图的路网上的过程。它的主要目的是跟踪车辆,交通流进行分析和发现驾驶方向的起点。
究其根本,是因为GPS给定的用户或者交通工具的位置信息(经度,纬度)在匹配到电子地图的路网上会有误差,如果不进行地图匹配,那么交通工具可能不显示路网上(例如路旁边的房屋里,或者池塘里等等),引用09年GIS论文[Map-matching for low-sampling-rate GPS trajectories][2]中的例子,如图,
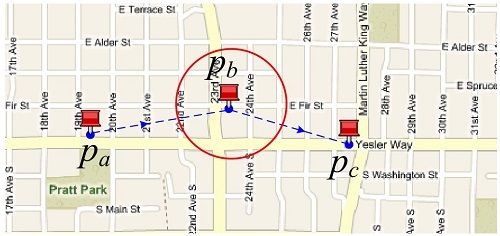
在Figure 1中,$P_a, P_b, P_c$ 是GPS设备定位到的位置信息,可以看出点 $P_b$ 里最近的路也有段距离,如果不做处理,这个点就定位到建筑中了,显然这是不合理的,所以我们需要对这个信息进行一定处理,是它能够较为精确地匹配到路网上。我个人觉得可以将Map-matching看作是LBS应用中的轨迹数据处理的数据预处理步骤,只有处理好这步,以后的研究才能有效地进行。直观地,最简单的方法,就是将GPS点关联到最近的路段上,但有些时候效果会非常差,例如可能3个连续的点,第一个点和第二个点都在一条路上,而第二个点因为误差,定位到另外一条无关的路,但却是是最近的。当然现在有很多方法已经能够很好的处理这个问题,比较著名的方法就是基于隐马尔科夫模型(HMM,之后用缩写表示)的,其正确率在几年的会议论文中结果在一定条件下都已经能够达到90%。
3. 隐马尔科夫模型(HMM)
3.1. HMM简述
HMM已经在应用在许多领域中,比较常见的应用有语音识别,词性标注等,具体的HMM可以参见wikipedia的描述以及Andrew NG教授的公开课Machine Learning,更多的资料大家可以Google,百度,像52nlp里描述的都是很好的,我以后可能也要写一篇关于HMM的博客。 这里简单介绍下HMM, 讲到隐马尔可夫模型,肯定首先要知道马尔科夫链, 在给定当前知识或信息的情况下,只有当前的状态用来预测将来,过去(即当前以前的历史状态)对于预测将来(即当前以后的未来状态)是无关的。用公式表示即:
$$P(X_{n+1}=x|X_0,X_1,X_2,…,X_n) = P(X_{n+1}|X_n),$$ $X_n$ 的值则是在时间 $n$ 的状态,也就是说在知道状态 $X_{n}$ 的前提下,$X_{n+1}$ 的状态只跟 $X_n$ 有关,跟之前的 $(n-1)$ 个状态是无关的. 举个不是很合适的例子就是,今天的天气只跟昨天的天气有关,跟昨天之前的天气无关,当然这是一个很强的假设前提。注:这里所说的马尔科夫链是一阶马尔科夫链,当然可以扩展出去二阶马尔科夫,三阶马尔科夫等等,这里不做过多描述。
而所谓的隐马尔科夫模型就是上述马尔科夫的状态是不可见的,而受状态影响的某些变量是可见,即我们能看的现象。如图Figure 2,$x_{t-1}$,$x_t$,$x_{t+1}$ 符合马尔科夫过程,但是我们是观察不到的,而 $y_{t-1}$, $y_t$, $y_{t+1}$ 是能够观察到的变量,但受各自的状态变量影响。

从上述说明以及Figure 2, 这里列举HMM的5个基本要素:
- HMM的状态变量数目:$N$
- HMM的观察变量数目:$M$
- 状态转移概率矩阵:$A=\left[ a_{ij}\right]_{N \times N}$, 其中 $a_{ij}=P(q_{t+1}=j|q_t = i), 1 \leq i, j \leq N$
- 观测概率矩阵:$B = \left[ b_j(k)\right]_{N \times M}$, 其中 $b_j(k) = P(o_t = o_k|q_t = j), 1 \leq j \leq N, 1 \leq k \leq M$
- 初始状态概率向量 $\pi=(\pi_i)$:$\pi_i = P(q_1 = i), 1 \leq i \leq N$
HMM有三个典型(canonical)问题:
- 概率计算问题:已知模型参数,计算某一特定输出序列的概率.通常使用Forward算法解决;
- 预测问题或者解码(decoding)问题:已知模型参数,寻找最可能的能产生某一特定输出序列的隐含状态的序列。通常使用Viterbi算法解决;
- 学习问题:已知输出序列,寻找最可能的状态转移以及输出概率。通常使用Baum-Welch算法。
上述三个问题不懂的可以先略过,或者参见详细的HMM资料,而且在下面相关论文工作中会说明在这几篇论文中其实只用到了预测问题的Viterbi算法,下面也会另开一小节具体描述下Viterbi算法。
3.2. 基于HMM的Map-Matching
Map-Matching的两个变量:
- 从GPS设备中得到的位置信息(经度,纬度):HMM中观察变量;
- 拥有GPS设备的物体(车,人等)实际所在的位置:HMM中的隐藏状态变量,实际地图是不知道GPS设备的准确位置的。
这样就把Map-Matching问题与HMM结合起来了。从3.1节我们大致描述了HMM的三个基本问题,很明显三个问题在Map-Matching中有用的是两个问题:(1)预测问题;(2)学习问题。因为Map-Matching的问题的特殊性(这里需要说明的是,我其实也不非常确定,只能说自己猜测),例如前一个地点和后一个地点之间的关系是连续的(两个点之间的路线距离),GPS点与路网上的关系也是用距离来表示,而距离是连续的,所以用类似语音识别中的HMM的学习方法是不行的,在我看过的论文中都是用认为定义的规则去拟合历史的真实数据得到状态概率转移矩阵 $A$ 以及观测概率矩阵 $B$。在论文中,定义的规则要满足人的直观上的感觉,即人的先验知识,主要有以下两种:
- 观测概率:观测的GPS点离旁边路段上的位置越近,那么这个真实点在这个路段上的概率越大
- 状态转移概率:这里有两种解决思路:(1)前后两个真实的位置点的距离越近,那么状态转移的概率越大;或者(2)真实路段上的前后两个点的距离与GPS观测的前后两个点的距离越接近,状态转移概率越大。
在第四大节我们会详细介绍相关论文所使用的算法规则。
3.3. Viterbi算法
上面讲了基于HMM的Map-Matching算法学习模型参数的大概思路,那么解决了学习问题解决了,剩下的就是预测问题了。 这一小节,会介绍Viterbi算法。Viterbi算法[6]实际上一个动态规划(DP)算法解隐马尔可夫模型预测问题,即用动态规划求概率最大路径(最优路径),其原理就是:如果最优路径在时刻 $t$ 通过结点 $i_t^\ast$,那么这一路径从节点 $i_t^\ast$ 到终点 $i_T^\ast$ 的部分路径,对于从 $i_t^\ast$ 到 $i_T^\ast$ 的所有可能的部分路径来说,必须是最优的。迭代公式如下;
$$\delta_t(i) = \max_{i_1,i_2,…,i_{t-1}} P(i_t = i, i_{t-1},…,i_1,o_t,…,o_1|\lambda),\quad i = 1,2,…,N$$\begin{eqnarray*}
\delta_{t+1}(i) &=& max_{i_1,i_2,…,i_{t}} P(i_{t+1} = i, i_{t},…,i_1,o_{t+1},…,o_1|\lambda) \\
&=& \max_{1 \leq j \leq N}[\delta_t(j)a_{ji}]b_i(o_{t+1}),\quad i = 1,2,…,N; t = 1,2,…,T-1
\end{eqnarray*} 那么定义在时刻 $t$ 状态为 $i$ 的所有单个路径 $(i_1,i_2,…,i_{t-1},i_t)$ 中概率最大的路径的第 $t-1$ 个结点为:
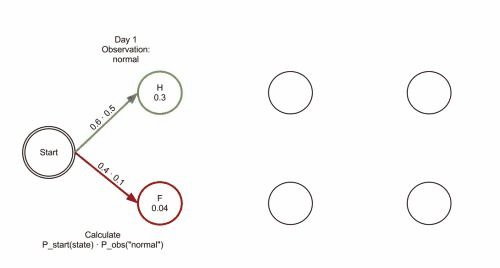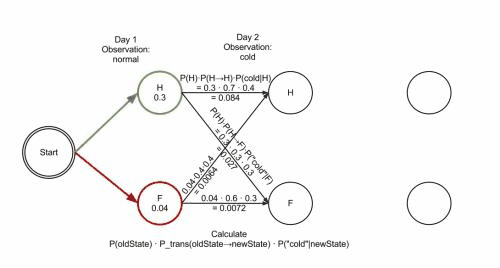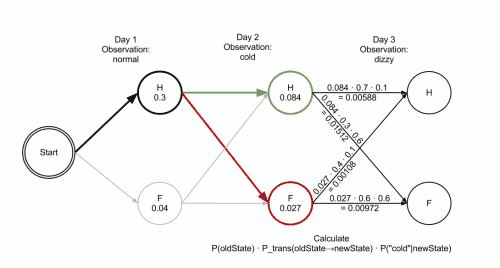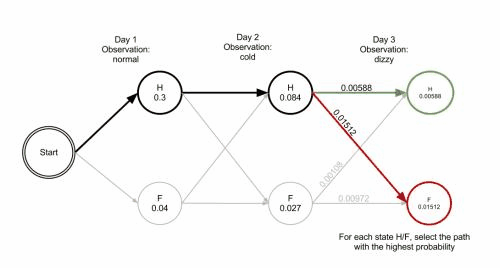
$$\Psi_t(i) = \arg \max_{1 \leq j \leq N}[\delta_{t-1}(j)a_{ji}],\quad i = 1,2,…,N$$上面公式所求的过程,当然迭代跟递归都是可以办到的。接下来看一个wiki上的Viterbi算法的democratic,如Figure 3所示,是一张Gif图片,每一层(每个时刻)要求出每个状态下符合观测变量的最大概率路径,然后再计算下一个时刻的值。
4. 相关部分论文工作
在之前的章节里,大概介绍了HMM以及HMM在Map-Matching 中的使用。在这里,我会列举几篇近几年关于这个主题的论文[1][2][3][4][5],会详细的介绍这些论文是怎样将HMM应用到Map-Matching中,即定义怎样的规则去拟合真实数据得到模型参数,主要依据是3.2中提到的那两点。下面依次介绍这五篇论文的内容(注:为了尊重原文,我尽量在公式中使用的是原文的符号形式,字母尽量按照本文中HMM出现的字母,大家可以一一跟上述的公式或者论文中的公式对应起来)
4.1. A HMM based MM for wheelchair navigation
从论文题目中就可以看出,这是关于轮椅导航的一篇论文[1],跟汽车导航不一样的是,轮椅的速度很慢,地点变化的频率较低,Map-matching处理能更简单,论文中也是简单的定义了规则求得状态转移矩阵 $A$ 和 观测概率矩阵 $B$。
- 首先是状态转移矩阵 $A$:$$a_{ij} = P(q_{t+1} = r_j| q_t = r_i)=e^{-r_{ij}}$$其中 $r_j$ 是时刻 $t+1$ 时所在路段,$r_i$ 是时刻 $t$ 时所在路段, 而 $r_{ij}$ 有三种不同的取值:(1)当路段 $r_j$ 与 $r_i$ 相邻时, $r_{ij} = 1$; (2)当路段 $r_j$ 与 $r_i$ 不相邻时,$r_{ij} = \infty$; (3)当路段 $r_j$ 与 $r_i$ 是同一个路段时,即 $i=j$ 时,$r_{ij} = 0$。上面三种情况对应的说明了在两个相邻时刻同一个路段行驶的概率大于前后两个时刻在两个相邻的路段行驶(譬如,每个路段10m),前后两个时刻分别出现在不相邻的路段上是不可能的(因为假设每个路段10m,时间间隔是1s,那么轮椅的速度是不可能超过10m/s的)。
- 观测概率矩阵 $B$:$$b_j(k) = P(o_t = o_k|q_t = r_j) = 1 / \frac{Distance \; from \; o_k \; to \; r_j}{\sum_{i=1}^n Distance \; from \; o_k \; to \; r_i}$$分母中所有的路段是选取那些以观测点 $o_k$ 为圆心画一定值(譬如10m)为半径的圆所相交的路段,从公式中能够很明显地看出其意图:离观测点越近的路段,其概率会越大。
4.2. MM for low-sampling-rate GPS trajectories
在这篇论文中,作者没有明确提出是基于HMM的,但是总结来看,论文中提出的模型可以算成HMM的变种。 此外, 论文还中考虑了路段的最大速率,以及自身在路段的平均速率。论文中使用了高斯分布来模拟观测概率转移,而状态转移概率则是综合了速率信息,观测点和隐藏实际点的信息计算出来,具体公式如下:
- 状态转移矩阵 $A$:$$a_{ij} = P(q_{t+1} = r_j | q_t = r_i) = V(r_i \rightarrow r_j)\cdot F_t(r_i \rightarrow r_j)$$ $$ F_t(r_i \rightarrow r_j) = \frac{d_{t \rightarrow t+1}}{w_{t \rightarrow t+1}} = \frac{||o_t-o_{t+1}||_{Euclidean\ Distance}}{||r_{i}-r_{j}||_{route}}$$ $$V(r_i \rightarrow r_j)= \frac{ \sum_{u=1}^k(e_u^\prime.v \times \bar{v}_{ij})} {\sqrt{\sum_{u=1}^k(e_u^\prime.v)^2} \times \sqrt{\sum_{u=1}^k{\bar{v}_{ij}}^2}}$$
其中 $F_t(r_i \rightarrow r_j)$ 是根据前后两个时间点之间的观测点和隐藏候选实际点的信息,$V(r_i \rightarrow r_j)$ 是前后两个时间点之间的速率信息;$||o_t-o_{t+1}||_{Euclidean\ Distance}$ 是观测点之间的欧几里德距离或者也可以是地球表明弧线距离,$F_t(r_i \rightarrow r_j)$ 表示如果前后两个观测点之间的距离与前后路段上两个候选点之间的距离的值越接近,那么实际点是这个两个候选点的概率越大;$V(r_i \rightarrow r_j)$ 中 $e_u^\prime.v$ 是路段的最大速率,$\bar{v}_{ij}$ 是平均速率, 公式表示平均速率与最大速率的变化程度相似,那么概率越大。 - 观测概率矩阵 $B$:$$b_j(k) = P(o_t = o_k|q_t = r_j) = \frac{1}{\sqrt{2\pi}\sigma }e ^{-\frac{||o_t- r_j||^2}{2\sigma^2}}$$ 很明显这里是用正态分布来拟合数据,时刻 $t$ 的观测点与候选点之间的距离越小,那么这个候选点是真正的实际点的概率就越大。
4.3. Hidden Markov MM through noise and sparseness
同4.2.节的文章一样,这篇文章也是发在2009年GIS的,同时两篇的内容也是相近的,这里讲下不同点:(1) 这篇文章没有考虑速率信息;(2) 它用前后两个观测点的距离与前后两个候选点的距离之差的绝对值来表示这两段距离的接近程度,越接近,概率越大,且最后的概率是用指数函数来拟合,因为在实际数据分析中,这个状态转移概率是符合指数分布的。而观测概率则是一模一样的,都是用了正态分布,具体公式如下(我就不一一解释了):
- 状态转移矩阵 $A$:$$a_{ij} = P(q_{t+1} = r_j | q_t = r_i) = \frac{1}{\beta}e^{\frac{-d_t}{\beta}}$$ $$d_t = |||o_t-o_{t+1}||_{great\ circle}-||r_{i}-r_{j}||_{route}|$$
- 观测概率矩阵 $B$:$$b_j(k) = P(o_t = o_k|q_t = r_j) = \frac{1}{\sqrt{2\pi}\sigma }e ^{-\frac{||o_t- r_j||^2}{2\sigma^2}}$$
4.2.和4.3.论文小结:其实仔细的人可以发现,这两篇论文中使用的模型不是完美的HMM,因为在计算状态转移概率时既要考虑候选点的信息,也要考虑观测点的信息,可以说是HMM的一个变种,所以在预测问题上对Viterbi算法也需要进行相应的改正。
4.4. MM with HMM on sampled road network
正是因为上面小结中所提到,它们使用的不是完美的最原始的HMM,这篇论文又将其模型简化,做出了一些实验,其实就是在计算状态转移概率时不考虑观测点之间的信息。在实验中,其效果跟4.3.的效果是差不多,甚至更好点。论文中公式如下:
- 状态转移矩阵 $A$:$$a_{ij} = P(q_{t+1} = r_j | q_t = r_i) \propto e^{-\beta d_t}$$ $$d_t = ||r_{i}-r_{j}||_{route}$$
- 观测概率矩阵 $B$:$$b_j(k) = P(o_t = o_k|q_t = r_j) = \frac{1}{\sqrt{2\pi}\sigma }e ^{-\frac{||o_t- r_j||^2}{2\sigma^2}}$$
4.5. Online MM based on HMM
在这篇论文中,与之前论文不同的创新点大概有三种:(1) 在计算状态转移矩阵时用了机器学习的方法:SVM;(2) 计算观测概率矩阵是考虑了路段的宽度信息;(3) 使用在线的Viterbi算法来达到在线的Map-Matching. 此外,这篇论文中的数据是包含时刻 $t$ 的速率和方向,即速度信息。
- 状态转移矩阵 $A$:两个feature,公式如下:
- The distance discrepancy function: $T(d_{i \rightarrow j},D_{i \rightarrow j}) = \frac{|d_{i \rightarrow j}-D_{i \rightarrow j}|}{D_{i \rightarrow j}} $
- The momentum change function: $M(\vec{v}_0,\vec{v}_1,\ell_1,…,\vec{v}_K,\ell_K) = \frac{\sum_i^K \ell_i|\vec{v_i}-\vec{v}_{i-1}|}{\bar{v}_{i\rightarrow j}\sum_i^K\ell_i}$
第一个公式中,$d_{i \rightarrow j}$ 表示前后两个时刻的平均速率乘以时间的距离,而 $D_{i \rightarrow j}$ 是前后两个时刻的两个候选点直接的最短路程的距离, 这个公式说明这两个距离越近越好。而第二个公式表示的动量的变化,利用类似以前高中物理学中的动量变化,只是这里是长度乘以速度,注:这里的 $\vec{v}_0,\vec{v}_1,…,\vec{v}_K$是候选路段上的各个速度,符合线性分布求得,这是假设前提。当然这两个公式算出来的都只是一个feature,之后还要利用标注好的数据利用SVM进行二类分类训练
- 观测概率矩阵 $B$:$$b_j(k) = P(o_t = o_k|q_t = r_j) = S(v_t,v_r)P(observation)$$ $$S(v_t,v_r) = \frac{v_r}{\max (0, v_t-v_r) + v_r}$$ $$P(observation) = \frac{1}{2w} \int_{-w}^{w} \frac{1}{\sqrt{2\pi}\sigma }e ^{-\frac{(\ell-d)^2}{2\sigma^2}}d\ell$$
$S(v_t,v_r)$ 其作用跟4.2.节中的速率变化功能是一样的,其中 $v_r$ 是最大速率,而 $P(observation)$ 考虑的路段的宽度信息,$2w$ 是路段宽度,同样使用高斯分布拟合。 - Online Viterbi算法讨论,如图:

从图中就可以很明显的看出,这个算法就是在递归的时候进行pruning,提前终止递归,如图中的红点时就停止了。不过,这里我有一点疑问,如果使用在线计算,那么用迭代的Viterbi算法,在 $t$ 时刻,只需要记住 $t-1$ 时刻的最大概率点不久完事了,为什么还要这样多此一举。
5.总结及将来工作
在这篇博客中,具体介绍了当前使用隐马尔可夫模型(HMM)对Map-Matching问题进行建模,列举了5篇近期论文,基本上都是属于基于规则的计算了状态转移概率和观察概率,且在每篇论文实验中都表明了这个方法的有效性。现阶段存在的问题就是数据集不统一,各个方法之间也没有进行对比好坏,几乎每篇论文都是用自己的数据集,自己的方法进行测试。那么以后有一个标准的测试集是一个重要问题。
之后的博客中,我会再进行一些相关工作的学习研究,并且看下除了利用HMM以外的方法进行Map-Matching。
6. 参考文献
[1]:Ren M, Karimi H A. A hidden Markov model-based map-matching algorithm for wheelchair navigation[J]. Journal of Navigation, 2009, 62(03): 383-395.
[2]:Lou Y, Zhang C, Zheng Y, et al. Map-matching for low-sampling-rate GPS trajectories[C]. Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. ACM, 2009: 352-361.
[3]:Newson P, Krumm J. Hidden Markov map matching through noise and sparseness[C]. Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. ACM, 2009: 336-343.
[4]:Raymond R, Morimura T, Osogami T, et al. Map matching with hidden Markov model on sampled road network[C]. Pattern Recognition (ICPR), 2012 21st International Conference on. IEEE, 2012: 2242-2245.
[5]:Goh C Y, Dauwels J, Mitrovic N, et al. Online map-matching based on hidden markov model for real-time traffic sensing applications[C]. Intelligent Transportation Systems (ITSC), 2012 15th International IEEE Conference on. IEEE, 2012: 776-781.
[6]:李航.统计学习方法.北京:清华大学出版社,2012