弱监督论文阅读：BoxLevelSet算法笔记

标题：Box-Supervised Instance Segmentation with Level Set Evolution
会议：ECCV2022
论文地址：https://link.springer.com/10.1007/978-3-031-19818-2_1

Abstract

相比于使用像素级掩码标注的全监督方法，边界框监督实例分割利用简单的边界框标注的优势，最近引起了大量研究关注。本文我们提出一种新颖的单阶段边界框监督实例分割方法，巧妙地将经典的水平集模型与深度神经网络相结合。具体来说，我们提出的方法通过一个连续的Chan-Vese能量函数以端到端的方式迭代学习一系列水平集。采用简单的掩码监督的SOLOv2模型预测实例感知的掩码图作为每个实例的水平集。输入图像及其深度特征都作为演化水平集曲线的输入数据，其中，一个边界框投影函数用于获得初始边界。通过最小化完全可微的能量函数，每个实例的水平集在其对应的边界框标注内迭代优化。在4个具有挑战性的基准测试集上的实验结果证明了我们提出的方法在各种场景下鲁棒实例分割的领先性能。

1 Introduction

实例分割旨在获取感兴趣目标的像素级标签，在自动驾驶、机器人控制等诸多应用中发挥着重要作用。尽管取得了良好的性能，但现有的实例分割方法大多以监督的方式进行训练，严重依赖像素级的掩码标注，并且需要高昂的标注成本。
为了解决这个问题，边界框监督实例分割利用简单的边界框标注而不是像素级的掩码标签，最近引起了大量研究关注。为了实现基于边界框标注的像素级监督，一些方法侧重于通过独立的网络生成伪掩码标签，这需要使用额外的辅助显著性数据或者MCG和CRF等后处理方法来获得精确的伪标签。由于涉及多个单独的步骤，训练pipeline因大量超参数而变得复杂。最近的一些方法提出使用成对亲和（pairwise affinity）建模的统一框架，例如相邻像素对和颜色对，从而实现实例分割网络的端到端训练。成对亲和关系定义在部分或所有相邻像素对的集合上，这过度简化了鼓励像素或颜色对共享相同标签的假设。来自外观相似的目标和背景的噪声上下文不可避免地被吸收，导致实例分割性能较差。
在本文中，我们提出一种新颖的单阶段边界框监督实例分割方法来克服上述局限性。我们的方法巧妙地将经典的水平集模型与深度神经网络相结合。与现有的边界框监督方法不同，我们以端到端的方式在标注的边界框内迭代学习一系列隐式曲线演化的水平集函数。与基于全监督水平集的方法不同，我们提出的方法能够以弱监督的方式仅利用原本用于目标检测的边界框标注来训练水平集函数。
具体来说，我们在经典的连续Chan-Vese能量泛函的基础上引入一个能量函数，并利用一个简单有效的掩码监督方法SOLOv2来预测实例感知的掩码图作为每个实例的水平集。除输入图像外，引入具有远程依赖的深层结构特征，使水平集曲线向目标边界鲁棒演化，每一步的水平集曲线都是通过边界框投影函数初始化。通过最小化完全可微的能量函数，每个实例的水平集在其对应的边界框标注内迭代优化。在通用场景、遥感和医学图像等多种场景下，针对实例分割的四个具有挑战性的基准测试集进行了广泛的实验。先进的定性和定量结果证明了我们提出方法的有效性。特别地，在遥感和医学图像上，我们的方法比SOTA方法有很大的提升。
本文工作的亮点总结如下：

1. 我们提出了一种新颖的基于水平集演化的实例分割方法。据我们所知，这是第一个基于深度水平集解决边界框监督实例分割问题的方法。
2. 我们将深层结构特征与低层图像相结合，在边界框区域内实现鲁棒的水平集演化，其中边界框投影函数用于水平集初始化。
3. 我们提出的方法在COCO和Pascal VOC数据集、遥感数据集iSAID和医学数据集LiTS上实现了SOTA的边界框监督实例分割。

2 Related Work

2.1 Box-Supervised Instance Segmentation

现有的实例分割方法大致可以分为两类。第一类是对检测结果中提取的区域进行分割。另一类直接以全卷积的方式对每个实例进行分割，不需要借助检测结果。然而，所有这些方法都依赖于高昂的像素级掩码标注。
仅使用边界框标注来获得像素级掩码预测的边界框监督实例分割最近受到越来越多的关注。Khoreva等人提出在深度学习框架下用边界框标注预测掩码，这在很大程度上依赖于GrabCut和MCG等无监督分割方法生成的区域提议。在Mask R-CNN的基础上，Hsu等人利用相邻像素对的亲和正则化将边界框监督实例分割问题转化为多实例学习（MIL）问题。BoxInst在一个高效的RoI-free的CondInst框架下使用具有边界框约束的颜色对亲和性。尽管性能很好，但成对亲和关系是建立在部分或所有相邻像素对上的，鼓励空间像素或颜色对共享相同的标签是过于简化的假设。这不可避免地引入了噪声，尤其是来自附近背景或相似目标的噪声。此外，最近的BBAM和DiscoBox等方法关注于代理掩码标签的生成，这些方法往往需要多个训练阶段或网络才能获得良好的性能。与上述方法不同，我们提出的基于水平集的方法是以端到端的方式隐式学习的，它能够通过优化边界框区域内的能量函数来迭代地对齐实例边界。

2.2 Level Set-Based Segmentation

作为经典的变分方法，水平集方法在图像分割中得到了广泛的应用，主要分为两类：基于区域的方法和基于边缘的方法。水平集的核心思想是将隐式曲线用更高维度的能量函数表示，通过梯度下降迭代优化。一些工作提出以端到端的方式将水平集嵌入到深度网络中，并取得了很好的分割效果。Wang等人通过结合用户对边界点的点击来预测演化参数并演化预测轮廓，能量函数采用此前文献中基于边缘的水平集方法。Levelset R-CNN在Mask R-CNN的基础上利用深度特征进行Chan-Vese水平集演化，优化时不使用原始图像。Yuan等人基于Mumford-Shah模型构建了一个分段常数函数来解析不同实例对应的各个常数子区域，通过全卷积网络实现实例分割。上述方法以全监督的方式在深度特征和真值掩码之间进行水平集演化，训练网络来预测不同的子区域并得到目标边界。我们提出的方法只使用基于边界框的标注进行水平集演化，而不使用像素级的掩码监督。
Kim等人以无监督的方式进行水平集演化，这与我们提出的方法是最相关的。为了实现N类语义分割，它使用只在输入图像的低层特征上演化的全局多相Mumford-Shah函数。我们的方法基于Chan-Vese泛函，它被约束在局部边界框内，包含了来自输入图像和高层深度特征的丰富信息。

3 Proposed Method

在本节，我们提出一种新颖的边界框监督实例分割方法，将经典的基于连续Chan-Vese能量的水平集模型融入到深度神经网络中。为此，我们引入一个能量函数，使得神经网络可以隐式地学习一系列演化到实例边界的水平集函数。具体来说，我们利用一种有效的掩码监督的SOLOv2模型，根据位置动态分割目标，并预测全图大小的实例感知掩码图。为了便于边界框监督的实例分割，将每个掩码图作为其对应目标的水平集函数$\varphi$。此外，我们同时利用输入图像$I_{img}$和高层深度特征$I_{feat}$作为输入来演化水平集，其中，一个边界框投影函数被用于鼓励网络在每一步自动估计一个初始的水平集${\varphi }_0$。每个实例的水平集在其对应的边界框标注内迭代优化。图1给出了我们提出的框架的概述。

3.1 Level Set Model in Image Segmentation

我们首先简要回顾水平集方法，它将图像分割表示为连续的能量最小化问题。在Mumford-Shah水平集模型中，一个给定图像$I$的分割是通过寻找一个参数轮廓$C$得到的，该轮廓$C$将图像平面$\Omega \subset {\mathbb{R}}^2$划分为$N$个不相交的区域${\Omega }_1,\cdot \cdot \cdot ,{\Omega }_N$。Mumford-Shah能量泛函${\mathcal{F}}^{MS}(u,C)$可以定义如下：
$${\mathcal{F}}^{MS}(u_1,\cdot \cdot \cdot ,u_N,{\Omega }_1,\cdot \cdot \cdot ,{\Omega }_N)=\sum _{i=1}^N({\int }_{{\Omega }_i}(I-u_i{)}^{2}dxdy+\mu {\int }_{{\Omega }_i}|\nabla u_i{|}^{2}dxdy+\gamma |C_i|)$$其中，$u_i$是用于逼近输入$I$的分段平滑函数，保证每个区域${\Omega }_i$内的平滑性。$\mu$和$\gamma$是权重参数。
Chan和Vese后来将Mumford-Shah泛函简化为一个变分水平集，得到了广泛的研究。具体的定义如下：
$${\mathcal{F}}^{CV}(\varphi ,c_1,c_2)={\int }_{\Omega }|I(x,y)-c_1{|}^{2}H(\varphi (x,y))dxdy+{\int }_{\Omega }|I(x,y)-c_2{|}^2(1-H(\varphi (x,y)))dxdy+\gamma {\int }_{\Omega }|\nabla H(\varphi (x,y))|dxdy$$其中，$H$是Heaviside函数，$\varphi (x,y)$是水平集函数，其过零点轮廓$C=\{(x,y):\varphi (x,y)=0\}$将图像空间$\Omega$分为两个不相交的区域，内轮廓$C:{\Omega }_1=\{(x,y):\varphi (x,y)>0\}$和外轮廓$C:{\Omega }_2=\{(x,y):\varphi (x,y)<0\}$。上式中，前两项的意思是拟合数据，第三项用非负参数$\gamma$正则化零水平轮廓。$c_1$和$c_2$分别是输入$I(x,y)$在$C$内和$C$外的平均值。通过寻找使能量${\mathcal{F}}^{CV}$最小的水平集函数$\varphi (x,y)=0$、$c_1$和$c_2$来实现图像分割。

3.2 Box-Supervised Instance Segmentation

我们提出的方法利用基于Chan-Vese能量模型的水平集演化来实现仅使用边界框标注的高质量实例分割。
边界框内的水平集演化。 给定一个输入图像$I(x,y)$，我们旨在通过在标注的边界框$\mathcal{B}$区域内隐式地演化一个水平集来预测目标的边界曲线。SOLOv2的掩码预测$M\in {\mathbb{R}}^{H\times W\times S^2}$包含$S\times S$个尺寸为$H\times W$的潜在实例图。每个潜在实例图只包含一个中心在位置$(i,j)$的实例。对于类别概率$p_{i,j}^{\ast }>0$的位置$(i,j)$，预测的掩码图被视为正实例样本。我们将边界框$\mathcal{B}$内的每个正掩码图视为水平集$\varphi (x,y)$，其对应的输入图像$I(x,y)$的像素空间称为$\Omega$，即$\Omega \in \mathcal{B}$。$C$是零水平的分割边界$C=\{(x,y):\varphi (x,y)=0\}$，它将边界框区域划分为两个不相交的区域，即前景目标和背景。
为了获得每个实例的精确边界，我们通过最小化下面的能量函数来学习一系列水平集$\varphi (x,y)$：
$$\mathcal{F}(\varphi ,I,c_1,c_2,\mathcal{B})={\int }_{\Omega \in \mathcal{B}}|I^{\ast }(x,y)-c_1{|}^2\sigma (\varphi (x,y))dxdy+{\int }_{\Omega \in \mathcal{B}}|I^{\ast }(x,y)-c_2{|}^2(1-\sigma (\varphi (x,y)))dxdy+\gamma {\int }_{\Omega \in \mathcal{B}}|\nabla \sigma (\varphi (x,y))|dxdy$$其中，$I^{\ast }(x,y)$表示归一化的输入图像$I(x,y)$，$\gamma$是非负权重，$\sigma$表示作为水平集$\varphi (x,y)$特征函数的sigmoid函数。不同于传统的Heaviside函数，sigmoid函数更加平滑，能够更好地表示预测实例的特征，促进训练过程中水平集演化的收敛。上式中，前两项迫使预测的$\varphi (x,y)$在内区域$\Omega$和外区域$\bar{\Omega }$都是均匀的。$c_1$和$c_2$分别是$\Omega$和$\bar{\Omega }$的平均值，定义如下：
$$c_1(\varphi )=\frac{{\int }_{\Omega \in \mathcal{B}}{I}^{\ast }(x,y)\sigma (\varphi (x,y))dxdy}{{\int }_{\Omega \in \mathcal{B}}\sigma (\varphi (x,y))dxdy},c_2(\varphi )=\frac{{\int }_{\Omega \in \mathcal{B}}{I}^{\ast }(x,y)(1-\sigma (\varphi (x,y)))dxdy}{{\int }_{\Omega \in \mathcal{B}}(1-\sigma (\varphi (x,y)))dxdy}$$在训练过程中，能量函数$\mathcal{F}$可以利用梯度反向传播进行优化。当时间步长$t\ge 0$时，能量函数$\mathcal{F}$对$\varphi$的导数可以写为：
$$\frac{\partial \varphi }{\partial t}=-\frac{\partial \mathcal{F}}{\partial \varphi }=-\nabla \sigma (\varphi )[(I^{\ast }(x,y)-c_1{)}^2-(I^{\ast }(x,y)-c_2{)}^2+\gamma div(\frac{\nabla \varphi }{|\nabla \varphi |})]$$其中，$\nabla$和$div$分别为空间梯度和散度算子。因此，$\varphi$的更新计算为：
$${\varphi }_i={\varphi }_{i-1}+\Delta t\frac{\partial {\varphi }_{i-1}}{\partial t}$$上述项的最小化可以看作是沿着能量函数下降的隐式曲线演化。通过迭代拟合${\varphi }_i$来最小化能量$\mathcal{F}$，得到实例的最优边界$C$，如下式：
$$\underset{\Omega \in \mathcal{B}}{\inf }\{\mathcal{F}(\varphi )\}\approx 0\approx \mathcal{F}({\varphi }_i)$$输入数据项。 能量函数$\mathcal{F}(\varphi ,I,c_1,c_2,\mathcal{B})$鼓励基于目标内外区域均匀性的曲线演化。输入图像$I_u$表示图像的基本底层特征，包括形状、颜色、图像强度等。然而，这些底层特征通常会随着光照变化、材质不同和运动模糊而变化，使得水平集演化的鲁棒性较差。
除了归一化的输入图像，我们考虑嵌入了图像语义信息的高层深度特征$I_f$，以获得更鲁棒的结果。为此，我们充分利用SOLOv2中来自所有FPN层的统一的高分辨率掩码特征$F_{mask}$，并将其进一步输入进一个卷积层来提取高层特征$I_f$。此外，特征$I_f$通过树滤波器进行增强，使用最小生成树建模远程依赖关系并保留目标结构。水平集演化的总能量函数可以表示如下：
$$\mathcal{F}(\varphi )={\lambda }_1\ast \mathcal{F}(\varphi ,I_u,c_{u_1},c_{u_2},\mathcal{B})+{\lambda }_2\ast \mathcal{F}(\varphi ,I_f,c_{f_1},c_{f_2},\mathcal{B})$$其中，${\lambda }_1$和${\lambda }_2$是平衡两类特征的权重。$c_{u_1}$、$c_{u_2}$和$c_{f_1}$、$c_{f_2}$分别是输入项$I_u$和$I_f$的平均值。
水平集初始化。 传统的水平集方法对初始化敏感，通常需要手动标注。在这项工作中，我们使用边界框投影函数来鼓励模型在每一步自动生成初始水平集${\varphi }_0$的粗略估计。
具体来说，我们利用真值框在$x$轴和$y$轴的的坐标投影，计算预测掩码图与真值框的投影差。这样的简单方案将预测的初始化边界限制在边界框内，为曲线演化提供了良好的初始状态。令$m^b\in \{0,1{\}}^{H\times W}$表示真值框中的位置为1否则为0的二值区域。每个实例的掩码分数预测$m^p\in (0,1{)}^{H\times W}$可视为前景概率。边界框投影函数$\mathcal{F}({\varphi }_0{)}_{box}$的定义如下：
$$\mathcal{F}({\varphi }_0{)}_{box}={\mathcal{P}}_{dice}(m_x^p,m_x^b)+{\mathcal{P}}_{dice}(m_y^p,m_y^b)$$其中，$m_x^p$、$m_x^b$和$m_y^p$、$m_y^b$分别表示掩码预测$m^p$和二值真值区域$m^b$的$x$轴投影和$y$轴投影。${\mathcal{P}}_{dice}$表示由一维dice系数度量的投影操作。

3.3 Training and Inference

损失函数。 训练我们提出网络的损失函数$L$由两项组成，包括用于类别分类的$L_{cate}$和用于边界框标注实例分割的$L_{inst}$：
$$L=L_{cate}+L_{inst}$$其中，$L_{cate}$是Focal Loss。对于$L_{inst}$，我们使用提出的可微水平集能量作为优化目标：
$$L_{inst}=\frac{1}{N_{pos}}\sum _k{\mathbb{I}}_{\{p_{i,j}^{\ast }>0\}}\{\mathcal{F}(\varphi )+\alpha \mathcal{F}({\varphi }_0{)}_{box}\}$$其中，$N_{pos}$表示正样本数，$p_{i,j}^{\ast }$表示目标位置$(i,j)$处的类别概率。$\mathbb{I}$表示指示函数，保证只有正实例掩码样本执行水平集演化。如果$p_{i,j}^{\ast }>0$则$\mathbb{I}$为1否则为0。$\alpha$是权重参数，在我们的实现中经验性地设置为3.0。
推理。 值得注意的是，水平集演化仅在训练时使用，来生成用于网络优化的隐式监督。推理过程与原始的SOLOv2网络相同。给定输入图像，用高效的矩阵非极大值抑制（NMS）直接生成掩码预测。与SOLOv2相比，我们提出的网络只引入了一个额外的卷积层来生成高层特征，其代价可以忽略不计。

4 Experiments

在COCO、Pascal VOC、遥感数据集iSAID和医学数据集LiTS上进行实验，训练过程仅使用边界框标注。

4.1 Datasets

介绍了这4个数据集。

4.2 Implementation Details

介绍了实现细节，$\mathcal{F}(\varphi ,I,c_1,c_2,\mathcal{B})$中的非负权重$\gamma$默认设置为$10^{-4}$。

4.3 Main Results

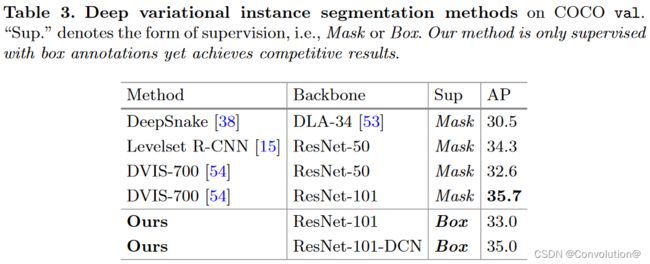
在COCO和VOC上的对比实验，$A{P}_s$略低是因为小目标缺乏丰富的特征用于水平集演化来区分边界框内的前景目标和背景。具体的实验结论可以参照原文。




在iSAID和LiTS上的对比实验。在遥感中，同一类的目标分布密集。对于医学图像，背景与前景高度相似。以往基于像素关系模型的方法都是建立在相邻像素对上，它们很容易受到噪声上下文的影响。我们的基于水平集的方法在水平集最小化的指导下驱动曲线去拟合目标边界，具有更强的鲁棒性。具体的实验结论可以参照原文。

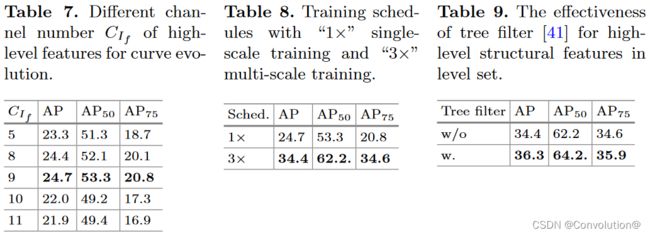
4.4 Ablation Experiments

消融实验，具体的实验结论可以参照原文。

5 Conclusion

本文提出了一种单阶段边界框监督实例分割方法，该方法以端到端的方式迭代学习一系列水平集函数。预测一个实例感知的掩码图并将其作为水平集，原始图像和深度高层特征都作为输入来演化水平集曲线，其中边界框投影函数用于获得初始边界。通过最小化完全可微的能量函数，每个实例的水平集在其对应的边界框标注内迭代优化。在4个具有挑战性的基准测试集上进行了广泛的实验，我们提出的方法在各种场景中表现出领先的性能。我们的工作缩小了全掩码监督和边界框监督实例分割之间的性能差距。