向量大小和归一化(vector magnitude & normalization)、向量范数(vector norm)、标量/向量/矩阵/张量
一、向量大小
首先一个向量![]() 的长度或者大小一般记为
的长度或者大小一般记为![]() 。上图中的平面向量
。上图中的平面向量![]() 的大小计算如下:
的大小计算如下:
![]()
空间向量![]() 的大小计算如下:
的大小计算如下:
![]()
![]() 维复向量
维复向量![]() 的大小计算如下:
的大小计算如下:
![]()
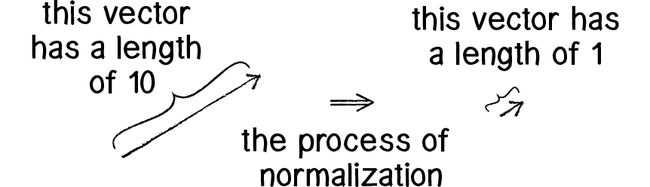
二、向量归一化
向量归一化即将向量的方向保持不变,大小归一化到1。向量![]() 的归一化向量
的归一化向量![]() 为:
为:
三、向量范数
范数是一种加强了的距离或者长度定义,比距离多一个数乘的运算法则。有时候范数可以当距离来理解。
0、![]() 范数,为向量
范数,为向量![]() 的所有元素非0的个数
的所有元素非0的个数
![]()
1、![]() 范数,为向量
范数,为向量![]() 的所有元素绝对值之和:
的所有元素绝对值之和:
对![]() 范数求优化解
范数求优化解![]() ,是想得到一个稀疏解。所以
,是想得到一个稀疏解。所以![]() 可以实现特征的稀疏(通过权重趋于0实现),去掉一些没有信息的特征,例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高、体重等可能关系不大,利用
可以实现特征的稀疏(通过权重趋于0实现),去掉一些没有信息的特征,例如在对用户的电影爱好做分类的时候,用户有100个特征,可能只有十几个特征是对分类有用的,大部分特征如身高、体重等可能关系不大,利用![]() 范数可以过滤掉。
范数可以过滤掉。
2、![]() 范数,为向量
范数,为向量![]() 的所有元素的平方和求正根:
的所有元素的平方和求正根:
对![]() 范数求优化解
范数求优化解![]() ,通常用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂,造成过拟合的现象,用来提高模型的泛化能力。
,通常用来做优化目标函数的正则化项,防止模型为了迎合训练集而过于复杂,造成过拟合的现象,用来提高模型的泛化能力。
3、![]() 范数,为向量
范数,为向量![]() 的所有元素的
的所有元素的![]() 次方之和开
次方之和开![]() 次方的正根:
次方的正根:
4、![]() 范数,为向量
范数,为向量![]() 的所有元素绝对值的最大值:
的所有元素绝对值的最大值:
![]()
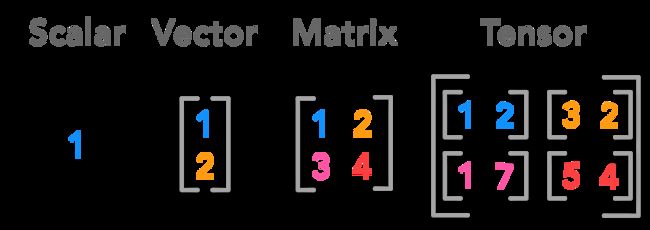
四、标量(Scalar)、向量(Vector)、矩阵(Matrix)、张量(Tensor)
标量是一个数值(1):
![]()
向量是一列数值(1*n),有大小和方向:
矩阵是二维的两列数值(m*n),表示一个面:
张量是多维的多列数值(m*n*h),可以表示多维空间(如3维,4维,5维...)。
注意,标量可以看成0维张量,向量看成1维张量,矩阵看成2维张量。
对于矩阵、张量的范数计算,可以分别拉平到向量应用向量范数计算公式得到。
import tensorflow as tf
import numpy as np
>>> v=tf.ones([3,3])
>>> v
>>> v1=tf.norm(v,ord=1)
>>> v1
>>> v2=tf.norm(v,ord=2)
>>> v2
>>> v3=tf.norm(v,ord=3)
>>> v3
>>> vinf=tf.norm(v,ord=np.inf)
>>> vinf
五、Keras的regularizers
1、![]()
#L1 class
tf.keras.regularizers.l1(l1=0.01, **kwargs)
The L1 regularization penalty is computed as: loss = l1 * reduce_sum(abs(x))2、![]()
#L2 class
tf.keras.regularizers.l2(l2=0.01, **kwargs)
The L2 regularization penalty is computed as: loss = l2 * reduce_sum(square(x))3、![]()
#l1_l2 function
tf.keras.regularizers.l1_l2(l1=0.01, l2=0.01)
Create a regularizer that applies both L1 and L2 penalties.
The L1 regularization penalty is computed as: loss = l1 * reduce_sum(abs(x))
The L2 regularization penalty is computed as: loss = l2 * reduce_sum(square(x))引用
【1】https://www.khanacademy.org/computing/computer-programming/programming-natural-simulations/programming-vectors/a/vector-magnitude-normalization
【2】https://hadrienj.github.io/posts/Deep-Learning-Book-Series-2.1-Scalars-Vectors-Matrices-and-Tensors/
【3】https://www.overleaf.com/learn/latex/Bold,_italics_and_underlining
【4】https://blog.csdn.net/nanhuaibeian/article/details/103727168
【5】https://blog.csdn.net/a493823882/article/details/80569888
【6】https://keras.io/api/layers/regularizers/
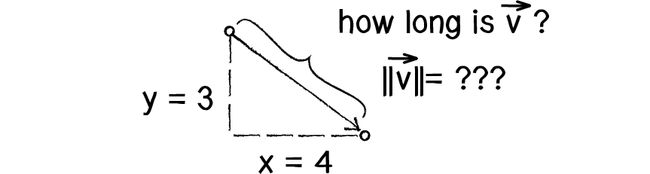

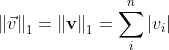
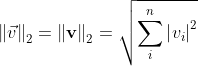
![\left \| \vec{v} \right \|_p=\left \| \bold{v} \right \|_p=\sqrt[p]{\sum_i^n\left |v_i \right |^p}](http://img.e-com-net.com/image/info8/9c003965d74741f381d7004bec298952.gif)