最优化算法----粒子群算法（PSO）

简介

粒子群算法($ParticleSwarmOptimization,PSO$)属于进化算法的一种，和模拟退火相似，也是从随机解出发，通过迭代寻找最优解，也是通过适应度来评价解的品质，比遗传算法规则更为简单，没有遗传算法的“交叉”和“变异”操作，通过追随当前搜索到的最优值来寻找全局最优。 实现容易，精度高，收敛快。

$PSO$在对动物集群活动行为观察基础上，利用群体中得到个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程，从而获得最优解。

原理

$PSO$ 中，每个优化问题的解都是搜索空间中的一只鸟，称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitness value)，每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子门就追随当前的最优粒子在解空间中搜索。

$PSO$ 初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中，粒子通过跟踪两个“极值”来更新自己。第一个就是粒子本身所找到的最优解，个体极值 $P_{id}$​。另一个就是整个种群目前找到的最优解，全局极值 $P_{gd}$ 。也可以不用整个集群而只是用其中一部分最为粒子的邻居，那么在所有邻居中的极值就是局部极值。

粒子公式：

在找到这两个最优值时，粒子根据如下的公式更新自己的速度和新的位置：
$$V_{id}=w{V}_{id}+C_{1}random(0,1)(P_{id}-X_{id})+C_{2}random(0,1)(P_{gd}-X_{id})$$

$$X_{id}=X_{id}+V_{id}$$

$V_{id}$ 是粒子的速度，$w$ 是惯性权重，$X_{id}$ 是当前粒子的位置，$P_{id}$ 表示第 $i$ 个变量的个体极值的第 $d$ 维， $P_{gd}$ 表示全局最优解的第 $d$ 维，$C_1$ 和 $C_2$ 为学习因子，前者为每个粒子的个体学习因子，后者为每个粒子的社会学习因子。$random(0,1)$ 表示区间 $[0,1]$ 上的随机数。

速度更新公式由三部分组成：第一部分为“惯性”或“动量”部分，反映了粒子的运动习惯，代表粒子有维持自己先前速度的趋势；第二部分为“认知”部分，反映了粒子对自身历史经验的记忆或回忆，代表粒子有向自身历史最佳位置逼近的趋势；第三部分为“社会”部分，反映了粒子间协同合作与知识共享的群体历史经验，代表粒子有向群体历史最佳位置逼近的趋势。

伪代码：

for each particle:
	initialize particle
while iter < maxIter:
    for each particle:
        calculate fitness value
        if the fitness is better than the best fitness value(P_id) in history:
            set current value as the new P_id
    choose the particle with the best fitness value of all the partivles as the gBest
    for each partile:
        calculate particle velocity according equation(1)
        update particle position according equation(2)
	if reach the expected optimal solution:
		break

在每一维粒子的速度都会被限制在一个最大速度$V_{max}$，如果某一维更新后的速度超过设定的 $V_{max}$，那么这一维度的速度被限定为$V_{max}$。

参数

粒子数： 一般取20~40，其实对于大部分问题10个粒子已经足够可以取得好的结果，不过对于比较难的问题或者特定类别的问题，粒子数可以取到100或200。

粒子的长度： 由优化问题决定，就是问题解的长度。

粒子的范围： 由优化问题决定，每一维可以设定不同的范围。

$V_{max}$ : 最大速度决定粒子在一个循环中最大的移动距离，通常设定为粒子的范围宽度。

学习因子： $C_1$ 和 $C_2$ 通常等于2，不过也有其他的取值，一般 $C_1=C_2\in [0,4]$。

终止条件： 最大循环数以及最小错误要求。

全局 $PSO$ 和局部 $PSO$ ：前者速度快不过有时会陷入局部最优，后者收敛速度慢一点不过很难陷入局部最优。在实际应用中，可以先用全局$PSO$ 找到大致的结果，再用局部$PSO$ 进行搜索。

惯性权重： 非负，惯性权重 $w$ 很小时偏重于发挥粒子群算法的局部搜索能力，惯性权重很大时教会偏重于发挥粒子群算法的全局搜索能力。

实验结果表明：在0.8~1.2之间，粒子群算法有较快的收敛速度；而当>1.2时，算法容易陷入局部极值。另外搜索过程中可以依据迭代进程及粒子飞行情况对惯性权重进行线性（或非线性）的动态调整，平衡搜索的全局性和收敛速度。在算法开始时，可赋予较大值，随着搜索的进行，可以逐渐减小，这样保证算法在刚开始各粒子都有较大的速度步长在全局范围内探测到较好的区域；而在后期，较小的权重则保证粒子能够在极值点周围做精细的搜索，从而使算法有较大的概率向全局最优解位置收敛。采用较多的动态惯性权重值是Shi提出的线性递减权值策略，表达式如下：
$$w=w_{max}-\frac{(w_{max}-w_{min})\ast t}{T_{max}}$$

其中，$T_{max}$ 表示最大迭代次数，$w_{min}$ 表示最小惯性权重，$w_{max}$ 表示最大惯性权重；$t$ 表示当前迭代次数。大多数应用中 $w_{max}=0.9,w_{min}=0.4$

对于更多的关于惯性权重的改进，可以查看这篇博客。

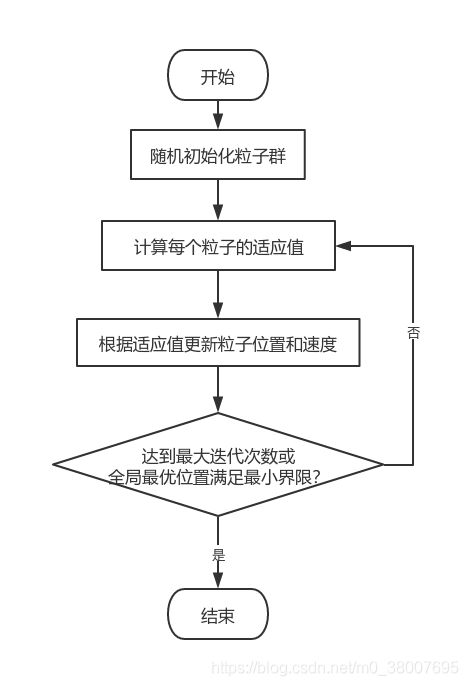
算法流程

初始化： 设置最大迭代次数，目标函数的自变量个数，粒子的最大速度，位置信息为整个搜索空间，在速度区间和搜索区间上随机初始化速度和位置，设置粒子规模，每个粒子随机初始化一个飞翔速度。

个体极值与全局最优解： 定义适应度函数，个体极值为每个粒子找到的最优解，从这些最优解找到一个全局最优解。与历史全局最优比较，进行更新。

终止条件： 1.达到设定的迭代次数；2.全局最优位置满足最小界限