数字信号处理 － Chap8 小波 （1）基础

8.1 基础

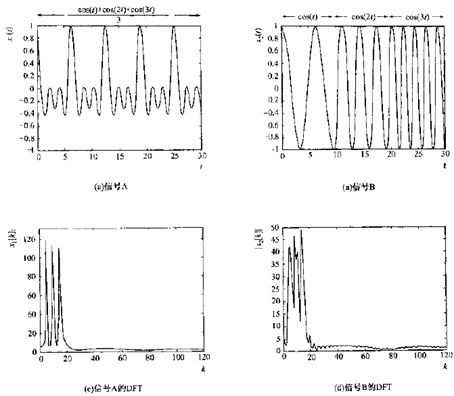
DFT可描述位于窗内的部分信号的频率，但是它不能识别各频率分量出现的时间。如下图所示，DFT的缺点就是不能将随时间变化的信号（非平稳信号）与不随时间变化的信号区（平稳信号）分开。

1）图a是历时30秒的信号A ，图b是依次10秒的cos(t)、cos(2t)、cos(3t)的信号B

2）对信号A和B都都以8采样点/秒进行采样，DFT的前120点如图b、c所示，尽管信号极不相同，但它们的频谱确很相似

 

                       

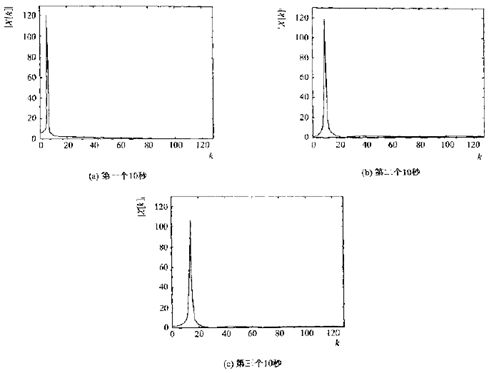
上面的问题也有解决办法，通过几个较短的窗（保证信号在每个窗内是平稳的），然后把从这些窗获得的频谱表示成时间序列，如下图

1）采样三个长度为10秒的窗加到上图b信号上，得到下面三个幅频

2）由于窗长度与信号各部分匹配得很好，所以下图的DFT每隔10秒得到一个单峰

                        

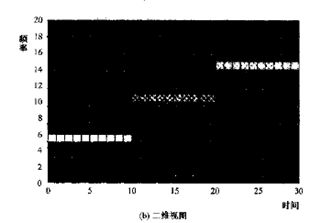
上图可合成为时间－频率图，横坐标是时间轴，单位为秒；纵坐标是频率轴，单位为DFT点；亮区域对应较强的响应。

             

 

虽然刚介绍的方法可提高DFT对非平稳信号的分析能力，但好的时间分辨率和好的频率分辨率不能同时获得，因此难以选择合适的窗长度。同时，选择合适的窗边界位置也很难。因此，用多个窗处理非平稳信号是不切实际的。

 

至此，主角小波该上场了，它用不同的分辨率分析信号中不同频率的分量。

1）对高频分量，采用高的时间分辨率（窄窗），因为此时信号变化快，需要重点了解信号出现和消失的时间

2）对低频分量，采用低的时间分辨率（宽窗），因为此时信号变化慢，较低的时间分辨率可以接受；同时可以获得较好的频率分辨率，使得低频信号能够识别。

为了实现不同频率上的不同分辨率，需要不同尺度的函数。函数 的尺度变化形式是 。若 代表基尺度，则有

1）S>1，得到较低频率的函数，表示基尺度的扩大，能够描述缓慢变化信号的趋势

2）S<1，得到较高频率的函数，表示基尺度的缩小，能够描述快速变化信号的细节

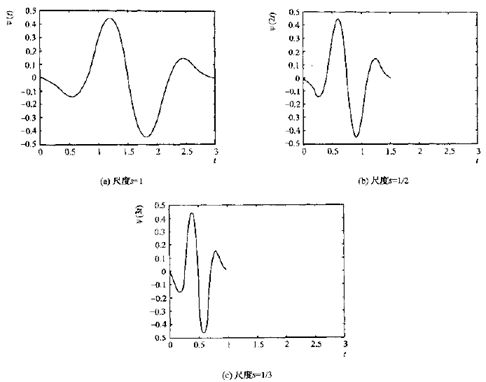
傅里叶级数将周期信号分解成无限多具有谐波关系的正弦和余弦，信号中低频分量响应于低频（大尺度）正弦波，高频分量响应于高频（小尺度正弦波）。小波同样具备这种频率局部化的特点，但与正弦波不同，它同时也是时间局部化的。有大量的小波族，每个族有独特的形状，且每族中基尺度仅覆盖一个固定的有限时间间隔。因此，小波能在时间和频率上提高好的分辨率，如下图所示的二阶样条小波：

1）图a为基尺度，该小波函数局部化于[0,3]时间内

2）尺度1/2和1/3的小波分别覆盖基尺度时间的1/2和1/3

3）这些尺度化的小波具有不同响应频率的函数族，且在时间和频率上都局部化

                              

为了分析信号中具有哪些频率分量以及它们在何时出现，每种尺度的小波函数要沿着时间平移，以与不同时间上的信号进行比较。小波函数的尺度和平移变换形式为 。如下所示，利用小波分析Sinc信号，尺度为1/2的小波与信号中间部分最吻合，，尺度为1/3的小波与信号两头最吻合。

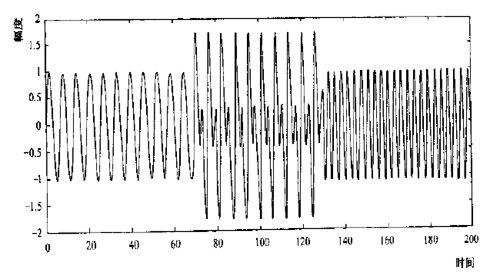
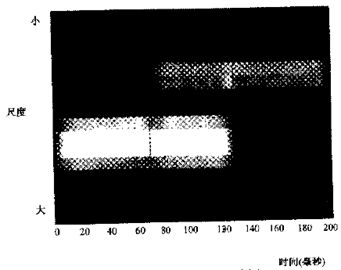
再看下面左图所示信号（0～130秒正弦波A，70～200秒正弦波B，中间两正弦波重叠），其小波时频图如下右图（低频出现在开始地方，高频出现中间到最后，中间地方两信号共存）