CF1681F Unique Occurences两种解法

传送门

---

Analysis

不妨设 $g(x)$ 为边权为 $x$ 的边被且仅被经过 1 次的路径个数。那么答案为 ${\sum }_{i=1}^{n}g(x)$。

接下来分析对于特定 $x$，如何去求得 $g(x)$。

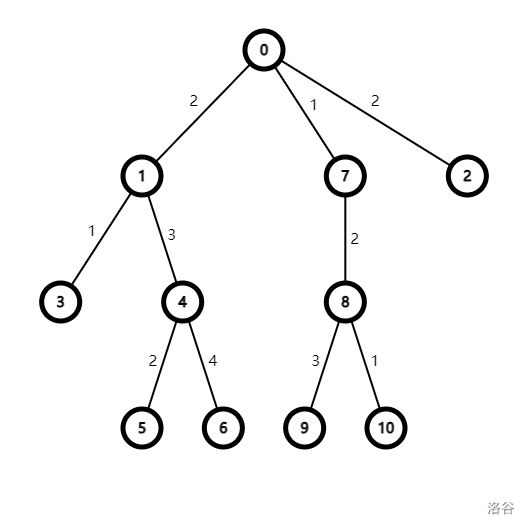
以这棵树为例，我们设当前要求 $g(2)$，即通过且仅通过边权为 2 的边一次的路径个数。

我们将所有边权为 2 的边删去，得到下图。

然后发现由于边的断开，这棵树分成了若干个连通块。观察发现，对于每条边权为 2 的边，它对答案的贡献就是它连接的两个连通块节点个数的乘积(确定路径的起点和终点)。

我们沿着这个思想，来考虑如何求得所有的 $g(x)$。

---

Solution 1

第一种解法是并查集分治。

要处理区间 $[l,r]$ 内所有边权的 $g(x)$ 之和，每次可以从中点将区间分成两半，递归求解左半段时，就将右半段所有边连上；递归求解右半段时，先把右半段所有边断开，再把左半段所有点连上。

这样当我们递归到某个确切的边权 $w$ 时，除了 $w$ 以外其他边权的所有边都连上了，对每个边权为 $w$ 的边求两个端点所在连通块节点个数的乘积。

这一过程可以用栈 + 并查集维护。并查集只能写按秩合并，不写路径压缩，否则无法撤销边。栈内存当前连上的所有边，递归结束回溯时就把栈内多出来的边都撤销。

因为并查集没有路径压缩，所以时间复杂度多了一个 $O(\log n)$。

Code

tourist 大神的现场代码 orz。

/**
 *    author:  tourist
 *    created: 23.05.2022 18:44:02       
**/
#include 

using namespace std;

#ifdef LOCAL
#include "algo/debug.h"
#else
#define debug(...) 42
#endif

int main() {
  ios::sync_with_stdio(false);
  cin.tie(0);
  int n;
  cin >> n;
  vector<vector<pair<int, int>>> g(n);
  for (int i = 0; i < n - 1; i++) {
    int a, b, c;
    cin >> a >> b >> c;
    --a; --b; --c;
    g[c].emplace_back(a, b);
  }
  vector<int> p(n);//并查集
  iota(p.begin(), p.end(), 0);
  vector<int> sz(n, 1);
  vector<pair<int, int>> ops;//栈，存储当前所有连起来的边
  auto Get = [&](int i) {//并查集找根
    while (i != p[i]) {
      i = p[i];
    }
    return i;
  };
  auto Unite = [&](int i, int j) {//按秩合并
    i = Get(i);
    j = Get(j);
    if (i != j) {
      if (sz[i] > sz[j]) {
        swap(i, j);
      }
      ops.emplace_back(i, p[i]);
      p[i] = j;
      ops.emplace_back(~j, sz[j]);
      sz[j] += sz[i];
    }
  };
  auto Rollback = [&](int T) {//撤销边
    while ((int) ops.size() > T) {
      int i = ops.back().first;
      int j = ops.back().second;
      ops.pop_back();
      if (i >= 0) {
        p[i] = j;
      } else {
        sz[~i] = j;
      }
    }
  };
  long long ans = 0;
  function<void(int, int)> Dfs = [&](int l, int r) {//分治函数
    if (l == r) {
      for (auto& p : g[l]) {
        int x = Get(p.first);
        int y = Get(p.second);
        ans += (long long) sz[x] * sz[y];
      }
      return;
    }
    int mid = (l + r) >> 1;
    {
      int save = (int) ops.size();
      bool fail = false;
      for (int i = mid + 1; i <= r; i++) {
        for (auto& p : g[i]) {
          Unite(p.first, p.second);
        }
      }
      Dfs(l, mid);
      Rollback(save);
    }
    {
      int save = (int) ops.size();
      bool fail = false;
      for (int i = l; i <= mid; i++) {
        for (auto& p : g[i]) {
          Unite(p.first, p.second);
        }
      }
      Dfs(mid + 1, r);
      Rollback(save);
    }
  };
  Dfs(0, n - 1);
  cout << ans << '\n';
  return 0;
}

时间复杂度：$O(n{\log }^{2}n)$

空间复杂度：$O(n)$

---

Solution 2

沿用同样的思想，但是我们考虑一次性 dfs 求出所有的 $g(x)$ 。

首先 dfs 一次预处理每个节点子树的节点个数 $s{z}_u$。

再次 dfs，过程中，对于每一个边权 $w$，记录 $cu{r}_w$ 表示当前所在的被 $w$ 分开的连通块编号、序列 ${x_w}_i$ 表示当前被 $w$ 分开的连通块中第 $i$ 个的节点数，以及 ${f{a}_w}_i$ 表示其父亲连通块的编号。

每次向下走，设经过的边权为 $w$，到达的节点为 $u$。就新产生了一个新的被边权为 $w$ 的边分开的连通块 ${x_w}_i=s{z}_u$，且 ${f{a}_w}_i=cu{r}_w$。同时令 ${x_w}_{cu{r}_w}\leftarrow {x_w}_{cu{r}_w}-s{z}_u$。下一步递归时 $cu{r}_w\leftarrow i$。

如此 dfs 完整棵树，就得到了所有边权对应的所有连通块，以及与之相邻的父亲连通块。

对所有边权 $w$，有 $g(w)={\sum }_i{x_w}_i\times {x_w}_{{f{a}_w}_i}$。

接下来放出鄙人现场写的拙劣的 AC 代码。

#include 
#define int long long
#define pb push_back
#define pii pair<int,int>
#define mp make_pair
#define F first
#define S second
using namespace std;
int n,ans,sz[500005],cur[500005];
vector<int> fa[500005],x[500005];
vector<pii> G[500005];//邻接表
void dfs0(int u,int p)//预处理每个子树节点个数
{
	sz[u]=1;
	for(auto pp:G[u])
		if (pp.F!=p)
		{
			int to=pp.F;
			dfs0(to,u);
			sz[u]+=sz[to];
		}
}
void dfs(int u,int p)//核心代码
{
	for(auto pp:G[u])
		if (pp.F!=p)
		{
			int to=pp.F,w=pp.S;
			x[w].pb(sz[to]);
			fa[w].pb(cur[w]);
			x[w][cur[w]]-=sz[to];
			int tmp=cur[w];
			cur[w]=(int)x[w].size()-1;
			dfs(to,u);
			cur[w]=tmp;
		}
}
signed main()
{
	ios::sync_with_stdio(false),cin.tie(nullptr);
	cin>>n;
	for(int i=0;i<n-1;i++)
	{
		int u,v,w;
		cin>>u>>v>>w;--u,--v,--w;
		G[u].pb(mp(v,w));
		G[v].pb(mp(u,w));
	}
	dfs0(0,-1);
	for(int w=0;w<n;w++)//初始化
		x[w].pb(sz[0]),fa[w].pb(-1);
	dfs(0,-1);
	for(int w=0;w<n;w++)
		for(int i=0;i<(int)x[w].size();i++)
			if (fa[w][i]!=-1)
				ans+=x[w][i]*x[w][fa[w][i]];//求答案
	cout<<ans<<endl;
	return 0;
}

时间复杂度：$O(n)$

空间复杂度：$O(n)$