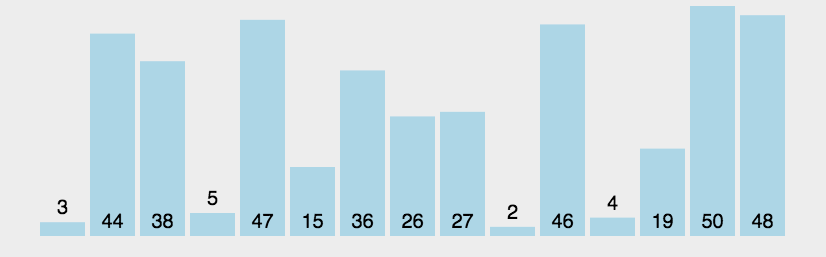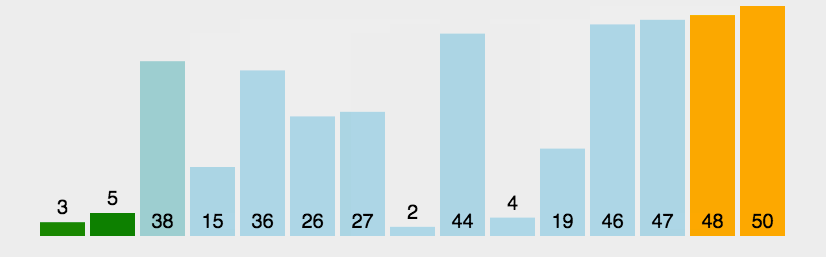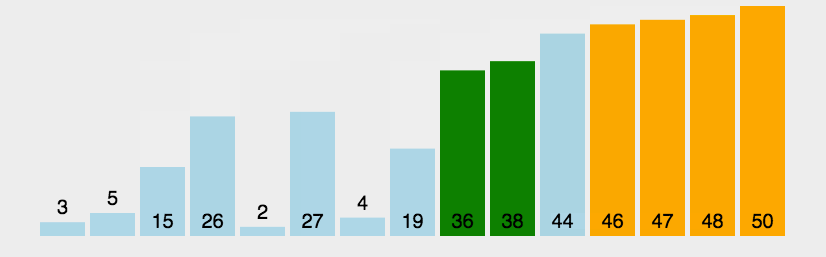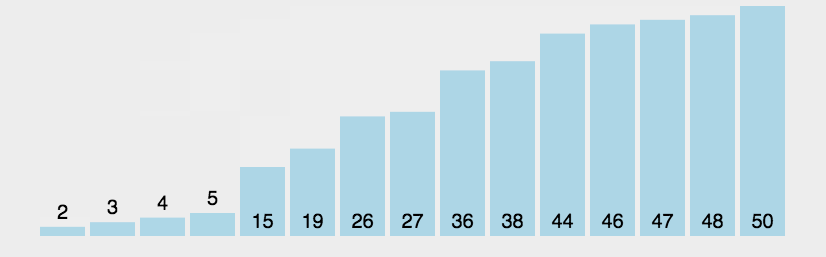Leetcode排序算法合集
文章目录
- 常用排序算法
-
- 快速排序(Quick Sort)
- 归并排序(Merge Sort)
- 插入排序(Insertion Sort)
- 冒泡排序(Bubble Sort)
- 选择排序(Selection Sort)
- 快速选择
-
- 215.数组中的第K个最大元素
- 桶排序
-
- 347.前 K 个高频元素
- 练习
-
- 451. 根据字符出现频率排序
- 75. 颜色分类
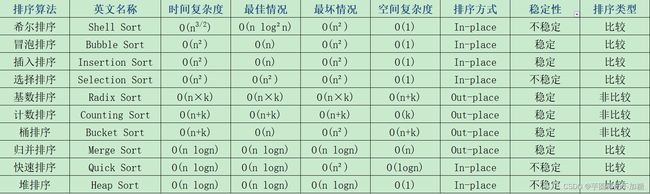
常用排序算法
在C++中可以通过std::sort()快速排序,刷题时很少需要自己手写排序算法,但是熟悉各种排序算法可以加深自己对算法的基本理解,以及解出由这些排序算法引申出来的题目。力扣101书中的内容较为精简,对于小白来说可能还需要再查阅资料,建议参考博客加深理解。
快速排序(Quick Sort)
快速排序采用分治法。首先从数列中挑出一个元素作为中间值。依次遍历数据,所有比中间值小的元素放在左边,所有比中间值大的元素放在右边。然后按此方法对左右两个子序列分别进行递归操作,直到所有数据有序。最理想的情况是,每次划分所选择的中间数恰好将当前序列几乎等分(均匀排布),整个算法的时间复杂度为O(n logn)。 最坏的情况是,每次所选的中间数是当前序列中的最大或最小元素(正序和逆序都是最坏),整个排序算法的时间复杂度为O(n²)。
平均时间复杂度为O(n logn),空间复杂度为O(logn),是一种不稳定的排序算法。
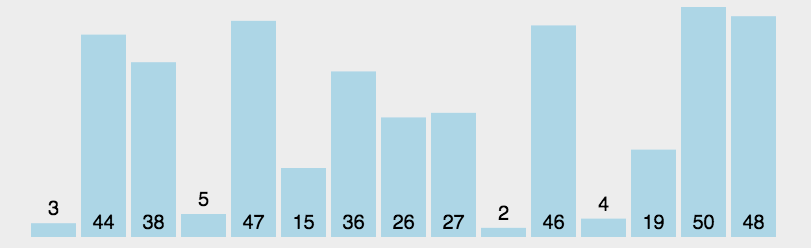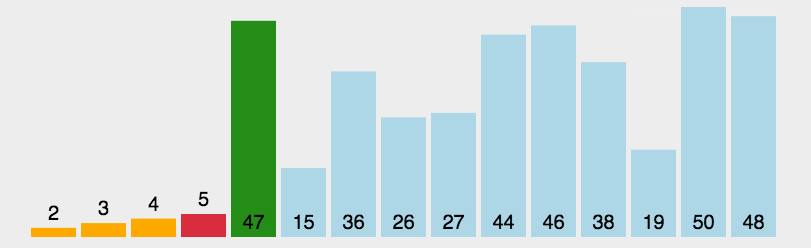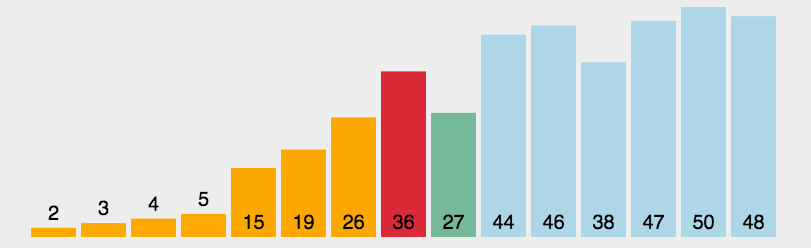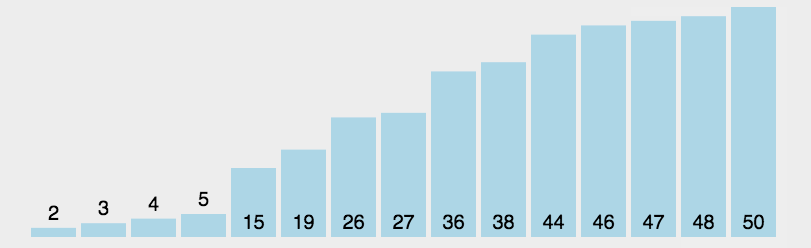
快速排序图解: 图源水印
(动图有点快,感觉脑子跟不上,可以看这个视频)
左闭右开的二分写法-代码:
void quick_sort(vector<int> &nums, int l, int r){
if (l + 1 >= r){//若待排序序列只有一个元素,返回空
return;
}
int first = l, last = r - 1, key = nums[first];//first作为指针从左到右扫描,记录着当前序列的左边界;last作为指针从右到左扫描,记录着当前序列的右边界,此处以第一个数作为基准数
//开始排序基准数
while (first < last){
//右指针先走
while (first < last && nums[last] >= key){//从右边找小于基准数的元素(此处由于last值可能会变,所以仍需判断first是否小于last)
--last;
}
nums[first] = nums[first];//找到则赋值
//左指针后走
while (first < last && nums[first] <= key){//从左边找大于基准数的元素(此处由于first值可能会变,所以仍需判断first是否小于last)
++first;
}
nums[last] = nums[first];//找到则赋值
}
nums[first] = key;//当first和last相遇,将基准元素复制到指针first处
//递归左、右序列
quick_sort(nums, l , first);//first左边的序列继续递归调用快排
quick_sort(nums, first + 1 , r);//first右边的序列继续递归调用快排
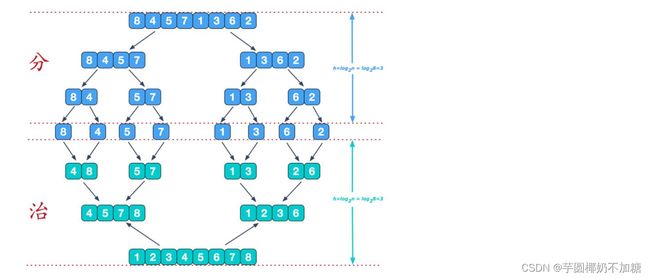
归并排序(Merge Sort)
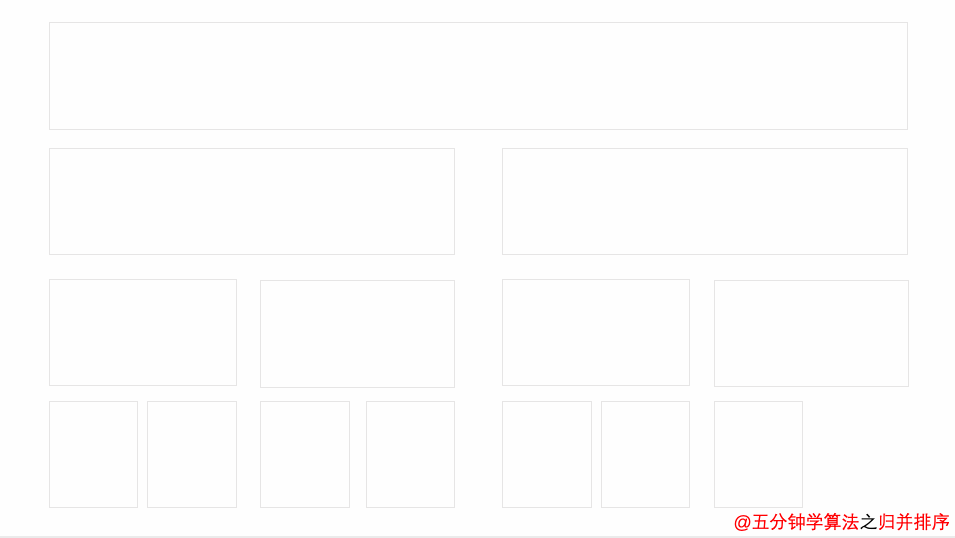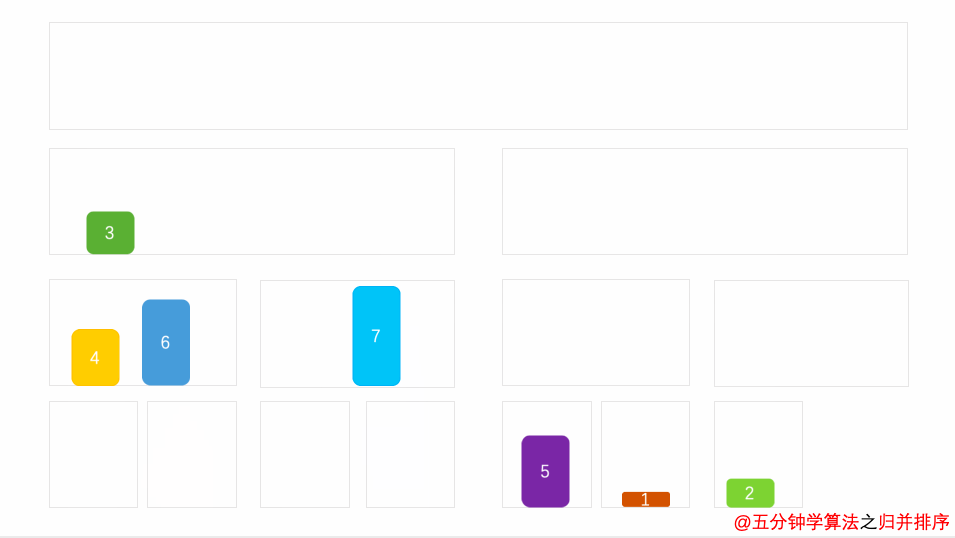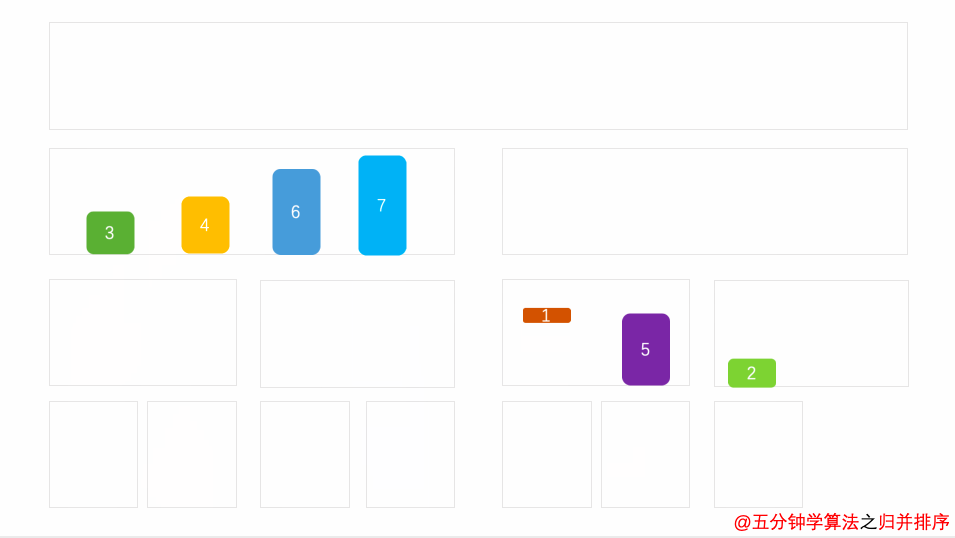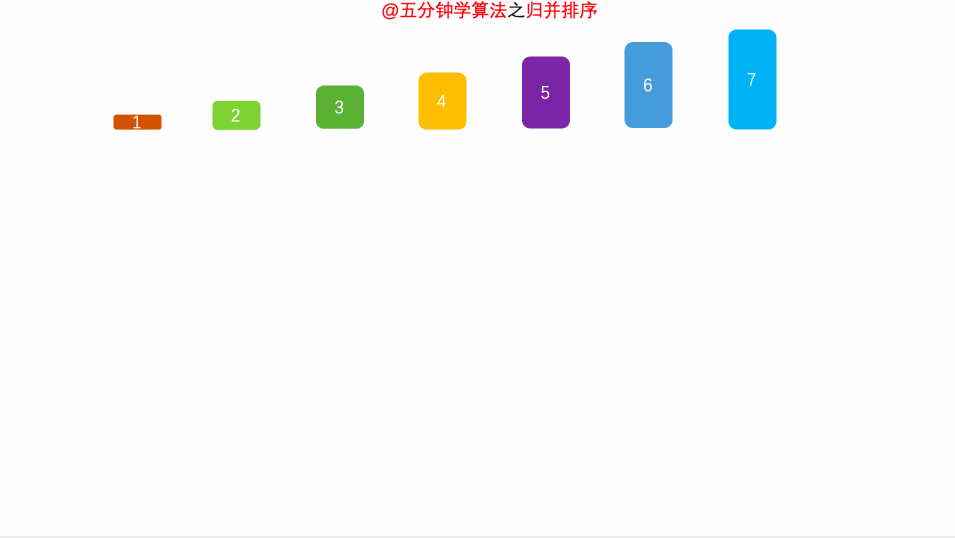
归并排序采用分治法,基本思想为将已有序的子序列合并,得到完全有序的序列。以二路归并为例,首先将整个数据样本拆分为两个子样本, 并分别对它们进行排序,拆分后的两个子样本序列,再继续递归的拆分为更小的子数据样本序列, 再分别进行排序, 直到最后数据序列长度为1无法拆分,最后将同一级别下的子数据样本两两合并在一起,直到所有数据有序。归并排序的终极优化版本为TimSort,最好情况下可将时间复杂度降至O(n)。还有一种改进的原地归并算法可牺牲部分时间效率将空间复杂度降至O(1)。
平均时间复杂度为O(n logn),空间复杂度为O(n),是一种稳定的排序算法。
代码:
void merge_sort(vector<int> &nums, int l, int r, vector<int> &temp) { //左闭右开,temp为辅助数组
if (l + 1 >= r) {
return;
}
// divide 分
int m = l + (r - l) / 2;
merge_sort(nums, l, m, temp);
merge_sort(nums, m, r, temp);
// conquer 治
int p = l, q = m, i = l;
while (p < m || q < r) {
if (q >= r || (p < m && nums[p] <= nums[q])) { //排序
temp[i++] = nums[p++];
} else {
temp[i++] = nums[q++];
}
}
for (i = l; i < r; ++i) { //将辅助数组的值返回到原数组
nums[i] = temp[i];
}
}
插入排序(Insertion Sort)
将前i个(初始为1)数据假定为有序序列,依次遍历数据,将当前数据插入到前述有序序列的适当位置,形成前i+1个有序序列,依次遍历完所有数据,直至序列中所有数据有序。数据是反序时,耗费时间最长O(n²);数据是正序时,耗费时间最短O(n)。适用于部分数据已经排好的少量数据排序。
平均时间复杂度为O(n²),空间复杂度为O(1),是一种稳定的排序算法。
插入排序图解:
代码:
void insertion_sort(vector<int> &nums, int n) {
for (int i = 0; i < n; ++i) {
for (int j = i; j > 0 && nums[j] < nums[j-1]; --j) {
swap(nums[j], nums[j-1]);
}
}
}
冒泡排序(Bubble Sort)
遍历所有的数据,每次对相邻元素进行两两比较,如果顺序和预先规定的顺序不一致,则进行位置交换;这样一次遍历会将最大或最小的数据上浮到顶端,之后再重复同样的操作,直到所有的数据有序。数据是反序时,耗费时间最长O(n²);数据是正序时,耗费时间最短O(n)。
平均时间复杂度为O(n²),空间复杂度为O(1),是一种稳定的排序算法。
代码:
void bubble_sort(vector<int> &nums, int n) {
bool swapped;
for (int i = 1; i < n; ++i) {//注意这个是从1开始
swapped = false;
for (int j = 1; j < n - i + 1; ++j) {//注意j的取值范围
if (nums[j] < nums[j-1]) {
swap(nums[j], nums[j-1]);
swapped = true;
}
}
if (!swapped) {
break;
}
}
}
选择排序(Selection Sort)
遍历所有数据,先在数据中找出最大或最小的元素,放到序列的起始;然后再从余下的数据中继续寻找最大或最小的元素,依次放到序列中直到所有数据有序。原始数据的排列顺序不会影响程序耗费时间O(n²),相对费时,不适合大量数据排序。
平均时间复杂度为O(n²),空间复杂度为O(1),是一种不稳定的排序算法。
代码:
void selection_sort(vector<int> &nums, int n) {
int mid;
for (int i = 0; i < n - 1; ++i) {
mid = i;
for (int j = i + 1; j < n; ++j) {
if (nums[j] < nums[mid]) {
mid = j;
}
}
swap(nums[mid], nums[i]);
}
}
以上排序代码调用方法为:
void sort() {
vector<int> nums = {1,3,5,7,2,6,4,8,9,2,8,7,6,0,3,5,9,4,1,0};
vector<int> temp(nums.size());
sort(nums.begin(), nums.end());
quick_sort(nums, 0, nums.size());
merge_sort(nums, 0, nums.size(), temp);
insertion_sort(nums, nums.size());
bubble_sort(nums, nums.size());
selection_sort(nums, nums.size());
}
快速选择
215.数组中的第K个最大元素
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
思路:
快速选择一般用于求解k-th Element 问题,可以在O(n) 时间复杂度,O(1) 空间复杂度完成求解工作。快速选择的实现和快速排序相似,不过只需要找到第 k 大的枢(pivot)即可,不需要对其左右再进行排序。与快速排序一样,快速选择一般需要先打乱数组,否则最坏情况下时间复杂度为O(n²),我们这里为了方便省略掉了打乱的步骤。
白话版本:快速排序每次排序会将基准数排到的位置,如果是从小到大排序,则第k大元素,就在num.size() - k的位置;如果是从大到小排序,则第k大元素,就在k - 1的位置。我们将基准数放到正确位置后,根据其位置,可以判断其是否是第k大元素。假定从大到小排序,如果基准数位置大于k - 1,我们继续往左排序即可,否则往右排序。
思路参考:https://leetcode.cn/problems/kth-largest-element-in-an-array/solution/you-xian-dui-lie-by-xiaocaigang-arcc/
代码:
class Solution {
public:
// 关于排序基准,试了三种方法,随机数、首位元素、两端和中间点取中值,结果是随机更快一点
int partition(vector<int>& nums, int left, int right) {
// 为了防止第一位元素是最小或者最大的那几个,取随机元素,尽量每次将区间对半分
int idx = rand() % (right - left + 1) + left;
swap(nums[left], nums[idx]);
int base = nums[left];
// 快速排序,注意是从大到小,因为我们找的是第K大
while (left < right) {
while (left < right && nums[right] <= base) {
--right;
}
nums[left] = nums[right];
while (left < right && nums[left] >= base) {
++left;
}
nums[right] = nums[left];
}
nums[left] = base;
return left;
}
int findKthLargest(vector<int>& nums, int k) {
srand(time(NULL));
int l = 0, r = nums.size() - 1;
// 迭代法实现,避免递归造成空间开销
while (l <= r) {//注意这里是小于等于
int pivot = partition(nums, l, r);
// 元素下标从0开始
if (pivot + 1 == k) {
return nums[pivot];
} else if (pivot + 1 < k) {
// 如果基准是前K大,第K大元素位于其右边
l = pivot + 1;
} else {
// 与上面相反
r = pivot - 1;
}
}
return 0;
}
};
桶排序
347.前 K 个高频元素
给你一个整数数组 nums 和一个整数 k ,请你返回其中出现频率前 k 高的元素。你可以按 任意顺序 返回答案。
示例 1:
输入: nums = [1,1,1,2,2,3], k = 2
输出: [1,2]
示例 2:
输入: nums = [1], k = 1
输出: [1]
思路: 桶排序
示例:
Input: nums = [1,1,1,1,2,2,3,4], k = 2
Output: [1,2]
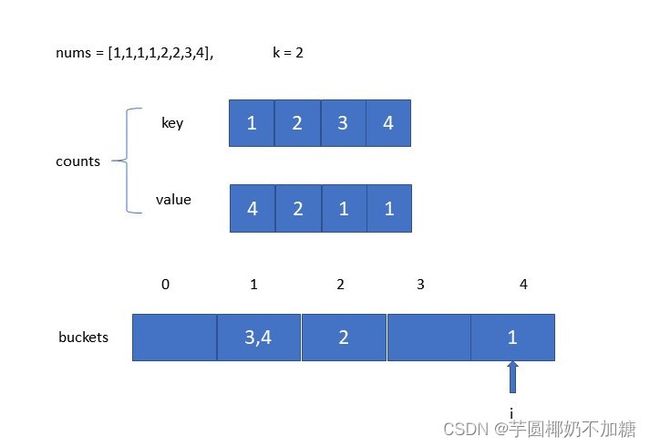
我们为每个值设立一个桶,桶内记录这个值出现的次数(或者其他属性),然后对桶进行排序。针对样例来说,我们先通过桶排序得到四个桶[1,2,3,4],它们的值分别为[4,2,1,1],表示每个数字出现的次数。
然后我们对桶的频次进行排序,前k个大的桶即是前k个频繁的数。这里我们可以使用各种排序算法,甚至可以再进行一次桶排序,把每个旧桶根据频次放在不同的新桶内。针对样例来说,目前最大的频次是4,我们建立[1,2,3,4]三个新桶,它们分别放入的旧桶为[[3,4],[2],[],[1]],表示不同数字出现的频率。最后,我们从后往前遍历,直到找到k个旧桶。
桶排序的时间复杂度为O(n)。
代码1-自做: 利用自带的sort函数会使时间复杂度为O(n log n),不符合题意
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
//考虑map数组储存
map<int, int> m;
for (int i = 0;i < nums.size();i++){
if (m.find(nums[i]) != m.end()) m[nums[i]]++;
else m.insert(pair<int, int>(nums[i],1));//如果没有该字符,则插入
}
//需要注意的是 map并没有像vector一样的sort函数
//解决方法:将map中的key和value分别存放在一个pair类型的vector中,然后利用vector的sort函数排序
vector<pair<int, int> > arr;
for (map<int, int>::iterator it = m.begin();it != m.end();++it){
arr.push_back(make_pair(it -> first,it -> second));//std::pair主要的作用是将两个数据组合成一个数据,两个数据可以是同一类型或者不同类型。
}
//比较函数
sort(arr.begin(), arr.end(), [](const pair<int, int>& a, const pair<int, int>& b){//要用常数 不然编译错误
return a.second > b.second;
});
//输出结果
vector<int> res(k);
for (int i = 0;i < k;i++){
res[i] = arr[i].first;//需要注意这里是first
}
return res;
}
};
代码2-桶排序:
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> counts; // 无序映射,用法count[key]=value
int max_count = 0;
for(const int & num : nums){ // for each循环遍历nums数组,每次遍历时把nums中的值赋给num
max_count = max(max_count, ++counts[num]); // 找出每个num出现频次最多的为多少次
}
vector<vector<int>> buckets(max_count + 1);//这里为什么要+1?可能是为了防止溢出
//vector> a(row,vector);定义一个row*column二维动态数组,并初始化为0,row必须定义
for(const auto & p : counts){
buckets[p.second].push_back(p.first);
// buckets[出现次数].push_back(当前元素);p.first为key值为num,p.second为value值为++counts[num]的值
}
vector<int> ans;
for(int i = max_count; i >= 0 && ans.size() < k; --i){ // 索引越高,所储存的数组中的元素出现的次数越多
for(const int & num : buckets[i]){
ans.push_back(num);
if(ans.size() == k){
break;
}
}
}
return ans;
}
};
练习
451. 根据字符出现频率排序
给定一个字符串 s ,根据字符出现的 频率 对其进行 降序排序 。一个字符出现的 频率 是它出现在字符串中的次数。
返回 已排序的字符串 。如果有多个答案,返回其中任何一个。
示例 1:
输入: s = “tree”
输出: “eert”
解释: 'e’出现两次,'r’和’t’都只出现一次。
因此’e’必须出现在’r’和’t’之前。此外,"eetr"也是一个有效的答案。
示例 2:
输入: s = “cccaaa”
输出: “cccaaa”
解释: 'c’和’a’都出现三次。此外,"aaaccc"也是有效的答案。
注意"cacaca"是不正确的,因为相同的字母必须放在一起。
示例 3:
输入: s = “Aabb”
输出: “bbAa”
解释: 此外,"bbaA"也是一个有效的答案,但"Aabb"是不正确的。
注意’A’和’a’被认为是两种不同的字符。
思路:
结合347思路理解,采用桶排序的话,思路是统计字符串中各字符的个数,然后进行按照次数装进桶中,最后从桶中取出各字符填入结果字符串中。
代码-桶排序:
class Solution {
public:
string frequencySort(string s) {
//桶排序的变形题
//注意字符串由大小写英文字母和数字组成
unordered_map<char, int> counts;
//统计字符串中各字符的个数
int max_count = 0;
int len = s.length();
for (int i = 0;i < len;i++){
if (counts.find(s[i]) != counts.end()) counts[s[i]]++;
else counts.insert(pair<char,int>(s[i],1));
max_count = max(max_count,counts[s[i]]);
}
//进行桶排序
vector<vector<int> > buckets(max_count + 1);
for (const auto & p : counts){
buckets[p.second].push_back(p.first);
}
//输出结果字符串
string ans = "";
for (int i = max_count;i >= 0;--i){
for (const char & ch : buckets[i]){//这里需要写一个函数:字符*i + 接到ans字符串后
int temp = i;
while(temp != 0){
ans.push_back(ch);
temp--;
}
}
}
return ans;
}
};
75. 颜色分类
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:
输入:nums = [2,0,1]
输出:[0,1,2]
思路:
这是经典的“荷兰国旗”问题。荷兰国旗由红、白、蓝三色组成。现在有若干个红、白、蓝三种颜色的球随机排列成一条直线。现在我们的任务是把这些球按照红、白、蓝排序。如下图所示。
原地排序就是不申请多余的空间来进行的排序。参考力扣题解,采用三路快排的方法。
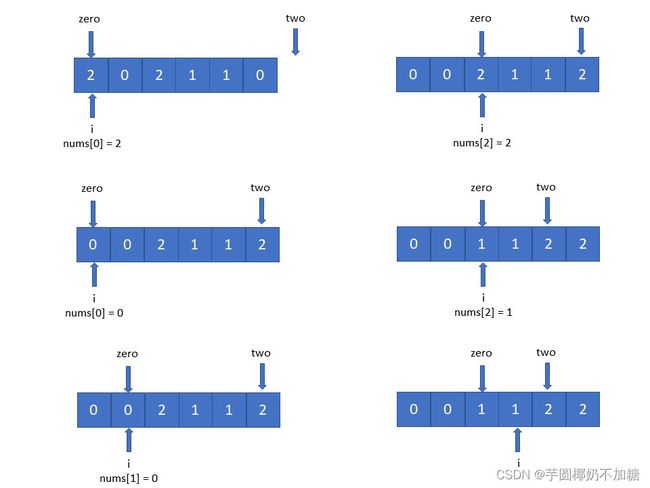
一次遍历,三路快排,双指针:用i遍历数组:[0...zero)是0,[two...len-1]是2,[zero...i)是1;
- 如果
nums[i] == 1,i++即可; - 如果
nums[i] == 0, 交换nums[i]和nums[zero],zero++,i++; - 如果
nums[i] == 2,two--,交换nums[i]和nums[two]。
图解:
代码1:
class Solution {
public:
void sortColors(vector<int> &nums) {
int size = nums.size();
if (size < 2) {
return;
}
// all in [0, zero) = 0
// all in [zero, i) = 1
// all in [two, len - 1] = 2
// 循环终止条件是 i == two,那么循环可以继续的条件是 i < two
// 为了保证初始化的时候 [0, zero) 为空,设置 zero = 0,
// 所以下面遍历到 0 的时候,先交换,再加
int zero = 0;
// 为了保证初始化的时候 [two, len - 1] 为空,设置 two = len
// 所以下面遍历到 2 的时候,先减,再交换
int two = size;
int i = 0;
// 当 i == two 上面的三个子区间正好覆盖了全部数组
// 因此,循环可以继续的条件是 i < two
while (i < two) {
if (nums[i] == 0) {
swap(nums[zero], nums[i]);
zero++;
i++;
} else if (nums[i] == 1) {
i++;
} else {
two--;
swap(nums[i], nums[two]);
}
}
}
};
完结撒花★,°:.☆( ̄▽ ̄)/$:.°★ 。