Python图像处理【10】基于离散余弦变换的图像压缩

0. 前言

由于图像中相邻像素间的相关性引起的空间冗余、图像序列中不同帧之间存在相关性引起的时间冗余，因此我们需要对图像数据进行压缩。数据压缩的目的就是通过去除这些数据冗余来减少数据表示所占用的存储空间。随着大数据时代的到来，图像数据在质量提高的同时，其大小也变得越来越大，在存储、传输、处理时非常困难，因此图像数据的压缩就显得非常重要。
图像压缩是数据压缩技术在图像上的应用，利用图像压缩可以减少图像数据中的冗余信息，从而能够更加高效存储和传输数据。在本节中，我们首先介绍离散余弦变换 (Discrete Cosine Transform, DCT) 的基本原理，利用 DCT 执行图像压缩操作，并实现图像 JPEG 压缩。

1. 离散余弦变换基础

离散余弦变换 (Discrete Cosine Transform, DCT) 以不同频率振幅的余弦函数组合表示图像，而离散傅里叶变换 (Discrete Fourier Transform, DFT) 则以复杂指数的形式使用正弦和余弦函数。以下方程式显示了如何计算 $N\times N$ 图像 $f(x,y)$ 的 DCT 的第 $(i,j)$ 项(系数)：

$$D(i,j)=\frac{1}{\sqrt{2N}}C(i)C(j)\sum _{x=0}^{N-1}\sum _{y=0}^{N-1}f(x,y)cos[\frac{(2x+1)i\pi }{2N}]cos[\frac{(2y+1)i\pi }{2N}]$$

其中 $C(u)=\{\begin{array}{rcl}\frac{1}{\sqrt{2}}& & u=0\\ 1& & u>0\end{array}$，对于块大小为 $8\times 8$ 的 DCT，$N=8$ 。

2. 基于离散余弦变换的图像压缩

DCT 算法用途广泛，通常用于实现图像 JPEG 压缩，在本节中，我们将学习如何使用 Python 执行图像重建操作。

(1) 首先，导入所需库，关键在于从 scipy.fftpack 模块导入所需的函数 dct() 和 idct()：

import scipy.fftpack as fp
from skimage.io import imread
from skimage.color import rgb2gray, gray2rgb
from skimage.draw import rectangle_perimeter
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D  # noqa: F401 unused import
from mpl_toolkits.axes_grid1 import make_axes_locatable
from matplotlib.ticker import LinearLocator, FormatStrFormatter
from scipy.fftpack import dct, idct

(2) 使用 scipy.fftpack 的 dct() 和 idct() 函数分别定义函数 dct2() 和 idct2() 以实现 2D-DCT 和 IDCT。其中，函数 dct() 的调用方式如下，而 idct() 函数的调用方式类似：

scipy.fftpack.dct(x, type=2, n=None, axis=-1, norm=None, overwrite_x=False)

该返回任意类型序列x的离散余弦变换。

根据在前言中介绍的 DCT 方程，并使用通过使用参数 norm ='ortho' 应用归一化：

def dct2(a):
    return dct(dct(a, axis=0, norm='ortho'), axis=1, norm='ortho')

def idct2(a):
    return idct(idct(a, axis=0, norm='ortho'), axis=1, norm='ortho')  

(3) 读取输入 RGB 图像并将其转换为灰度。计算图像的 2D-DCT，然后利用 IDCT 使用前面定义的函数重建图像：

im = rgb2gray(imread('1.png'))
imF = dct2(im)
im1 = idct2(imF)

(4) 检查重建的图像，观察其与原始图像之间的差别，查看其是否与原始图像相同，在这里使用函数 np.callclose() 评估图像间的差距：

print(np.allclose(im, im1))

(5) 使用 matplotlib.pyplot 绘制原始图像和重建图像，得到结果如下所示：

plt.figure(figsize=(10,5))
plt.gray()
plt.subplot(121), plt.imshow(im), plt.axis('off'), plt.title('original image', size=10)
plt.subplot(122), plt.imshow(im1), plt.axis('off'), plt.title('reconstructed image (DCT+IDCT)', size=10)
plt.tight_layout()
plt.show()

在以上结果图像中可以看到，重建后的图像与原始图像在视觉效果上类似，证明了可以使用 DCT 进行图像压缩，使用 IDCT 对压缩后的图像进行重建。

3. 图像 JPEG 压缩

在上一小节中，我们已经学习了如何实现 2D-DCT 和 IDCT，在本节中，我们将使用这两种技术执行图像压缩操作，完成 JPEG 格式图像压缩。

3.1 JPEG 压缩原理

JPEG 压缩基本操作步骤如下所示：

• 将图像分割为 8x8 的图像块
• 在每个图像块上(从左到右，从上到下)应用 DCT
• 对每个图像块使用量化压缩
• 将压缩后的图像块存储在较小的空间中，从而达到较高的压缩效果

下图显示了在 8x8 图像块的 64 个 DCT 基函数，对于图像中的每个块，64 个 DCT 系数是基函数的线性组合以生成图像块系数：

接下来，我们将实现简化版 JPEG 压缩，以确保仅需少数 DCT 系数可以表示图像，而不会导致图像质量有过多的视觉失真。在本节中，我们将直接在输入图像像素上计算 8x8 图像块的 DCT。此外，我们将使用全局阈值来清零大部分 DCT 系数，而不是通过用量化矩阵(对于给定的压缩级别)分割 DCT 矩阵来进行量化。最后，我们将跳过霍夫曼 (Huffman) 编码，并存储(压缩)/读取(解压缩)图像。

3.2 JPEG 压缩实践

(1) 导入所需库，读取输入图像，并将图像分割为 8x8 的 DCT 块：

import scipy.fftpack as fp
from skimage.io import imread
from skimage.color import rgb2gray, gray2rgb
from skimage.draw import rectangle_perimeter
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D  # noqa: F401 unused import
from mpl_toolkits.axes_grid1 import make_axes_locatable
from matplotlib.ticker import LinearLocator, FormatStrFormatter
from scipy.fftpack import dct, idct

def dct2(a):
    return dct(dct(a, axis=0, norm='ortho'), axis=1, norm='ortho')

def idct2(a):
    return idct(idct(a, axis=0, norm='ortho'), axis=1, norm='ortho')

im = rgb2gray(imread('1.png'))

dct_coeffs = np.zeros(im.shape)

for i in range(0, im.shape[0], 8):
    for j in range(0, im.shape[1], 8):
        dct_coeffs[i:(i+8),j:(j+8)] = dct2(im[i:(i+8),j:(j+8)])

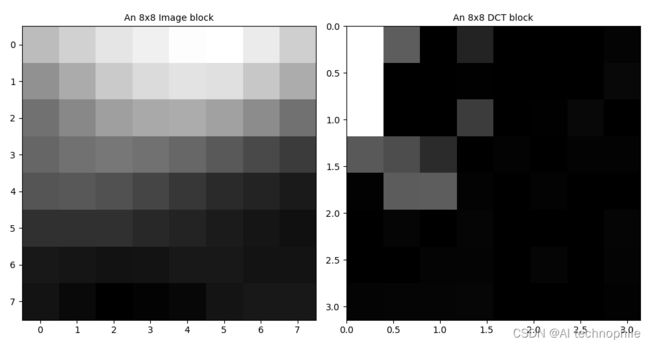
(2) 从图像中提取一个图像块，并显示该块的 DCT 系数。

index = 112
plt.figure(figsize=(10,6))
plt.gray()
plt.subplot(121), plt.imshow(im[index:index+8,index:index+8]), plt.title( "An 8x8 Image block", size=10)
plt.subplot(122), plt.imshow(dct_coeffs[index:index+8,index:index+8], vmax= np.max(dct_coeffs)*0.01, vmin = 0, extent=[0, np.pi, np.pi, 0])
plt.title("An 8x8 DCT block", size=10)
plt.show()

输出结果如下所示：

(3) 使用全局阈值对 DCT 系数进行阈值设置，将值小于阈值乘以最大系数值的所有 DCT 系数置为 0，打印应用阈值后剩余的非零 DCT系数的百分比。

thresh = 0.03
dct_thresh = dct_coeffs * (abs(dct_coeffs) > (thresh*np.max(dct_coeffs)))
percent_nonzeros = np.sum( dct_thresh != 0.0 ) / (im.shape[0]*im.shape[1])
print ("Keeping only {}% of the DCT coefficients".format(percent_nonzeros*100.0))
# Keeping only 3.45875% of the DCT coefficients

从以上输出可以看出，应用阈值后，只有约 3.5％ 的 DCT 系数为非零值。

(4) 可视化原始 DCT 系数以及阈值处理后获得的系数：

plt.figure(figsize=(12,7))
plt.gray()
plt.subplot(121), plt.imshow(dct_coeffs,cmap='gray',vmax = np.max(dct_coeffs)*0.01,vmin = 0), plt.axis('off')
plt.title("8x8 DCTs of the image", size=10)
plt.subplot(122), plt.imshow(dct_thresh, vmax = np.max(dct_coeffs)*0.01, vmin = 0), plt.axis('off')
plt.title("Thresholded 8x8 DCTs of the image", size=10)
plt.tight_layout()
plt.show()

(5) 最后，仅使用 3.5％ 非零 DCT 系数，使用 8x8 块 IDCT 重建压缩图像：

im_out = np.zeros(im.shape)
for i in range(0, im.shape[0], 8):
    for j in range(0, im.shape[1], 8):
        im_out[i:(i+8),j:(j+8)] = idct2( dct_thresh[i:(i+8),j:(j+8)])

(6) 绘制原始图像和 DCT 压缩图像，并对比原始图像和重建(压缩)图像：

plt.figure(figsize=(15,7))
plt.gray()
plt.subplot(121), plt.imshow(im), plt.axis('off'), plt.title('original image', size=10)
plt.subplot(122), plt.imshow(im_out), plt.axis('off'), plt.title('DCT compressed image', size=10)
plt.tight_layout()
plt.show()

从以上图像可以看到，仅通过有效地存储大约 3.5％ 的 DCT 系数，我们便可以高图像质量的重建图像，而不会过多的降低图像质量上，从而实现较高压缩比，并计算 MSE/PSNR 以进行定量测量图像间的差距。

小结

离散余弦变换 (Discrete Cosine Transform, DCT) 以不同频率振幅的余弦函数组合表示图像，而离散傅里叶变换 (Discrete Fourier Transform, DFT) 则以复杂指数的形式使用正弦和余弦函数。在实际应用中，DCT 算法用途广泛，通常用于实现图像 JPEG 压缩，在本节中，我们学习了如何利用 DCT 执行图像 JPEG 压缩，用于更加高效存储和传输图像数据。

系列链接

Python图像处理【1】图像与视频处理基础
Python图像处理【2】探索Python图像处理库
Python图像处理【3】Python图像处理库应用
Python图像处理【4】图像线性变换
Python图像处理【5】图像扭曲/逆扭曲
Python图像处理【6】通过哈希查找重复和类似的图像
Python图像处理【7】采样、卷积与离散傅里叶变换
Python图像处理【8】使用低通滤波器模糊图像
Python图像处理【9】使用高通滤波器执行边缘检测