python与人工智能：线性回归和逻辑回归

 线性回归

  线性回归是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，运用 十分广泛。

        

 梯度下降？

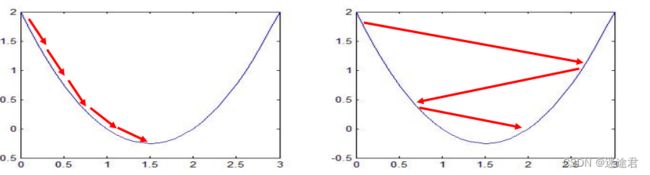
梯度下降法的基本思想可以类比为一个下山的过程。 假设这样一个场景：一个人被困在山上，需要从山上下来(例如： 找到山的最低点，也就是山谷)。但此时山上的浓雾 很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。 这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位 置最陡峭的地方，然后朝着山的高度下降的地方走，然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷

转换成计算机理解：

就是让计算机不断猜最小值的那个点自变量x在哪，猜大了让它小一点，猜小了让它大一点，也许猜个几万次就猜中了。 怎么猜的根据梯度猜的。梯度是啥，导数。怎么根据导数猜的？高中老师教过当前这个点导数大于0证明它周围单调增， 最小值点肯定比当前猜的这个点小，那我下次就猜小一点（因为我想找最小值点在哪）

我们同时可以假设这座山最陡峭的地方是无法通过肉眼立马观察出来的，而是需要一个复杂的工具来测量，同时，这 个人此时正好拥有测量出最陡峭方向的能力。所以，此人每走一段距离，都需要一段时间来测量所在位置最陡峭的方 向，这是比较耗时的。那么为了在太阳下山之前到达山底，就要尽可能的减少测量方向的次数。这是一个两难的选择， 如果测量的频繁，可以保证下山的方向是绝对正确的，但又非常耗时，如果测量的过少，又有偏离轨道的风险。所以 需要找到一个合适的测量方向的频率（学习率或者步长），来确保下山的方向不错误，同时又不至于耗时太多！

 下面我们用代码来演示一下：首先我们需要手动建立一个模型，并得到我们的数据集，然后用sklean框架中的线性回归方法，对这些数据进行学习训练得到一个假模型

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression

def load_data():
    # 先假设模型的 k=0.85 b=15
    x = np.random.uniform(0, 90, (200, 1))
    y = 0.9*x + 15
    # 将x, y在假模型直线附近呈正态分布
    x = np.random.normal(x, 6)
    y = np.random.normal(y, 6)
    return x, y

def drawScatter(xx, yy):
    plt.scatter(xx, yy, c='b')
    plt.show()

if __name__ == "__main__":
    # 获得数据集
    x, y = load_data()
    x_test = np.array([[40, ]])
    # 创建线性回归对象
    linear = LinearRegression()
    # 学习训练，得到模型
    linear.fit(x, y)
    # 根据模型预测y坐标
    y_pre = linear.predict(x_test)
    # coef_:保存模型的k值，intercept:保存模型的b值
    print("k:{} b:{}".format(linear.coef_, linear.intercept_))
    print("预测：", y_pre)
    print("真实：", 0.9*x_test+15)
    # 画出真实点和预测点
    plt.scatter(x_test, y_pre, c='y', marker="*")
    plt.scatter(x_test, 0.9*x_test+15, c='g', marker='s')
    plt.plot(x_test, linear.coef_ * x_test + linear.intercept_, c='r')
    drawScatter(x, y)

逻辑回归

        逻辑回归虽然被称为回归，但一般被用来处理二分类问题，它是将样本的特征和样本发生的概率联系起来，是一种监督学习的方法。

    """
        线性回归中，模型，y=kx+b
        逻辑回归中，k值有多个，b值有多个，那么模型为fx=k0*xx+k1*yy+b
        那么当fx=0时，概率为0.5表示当前（x,y）刚好在两个阵营的中间
        fx>0,表示1阵营，fx<0 表示为0阵营
    """

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
def load_data():
    xx = np.array([
        [0.1, 1.1],
        [0.25, 0.5],
        [0.28, 1.0],
        [0.48, 1.6],
        [0.85, 1.49],
        [0.91, 0.1],
        [1.2, 1.3],
        [1.5, 2.8],
        [2.0, 1.8],
        [1.2, 2.4],

        [0.3, 2.7],
        [0.5, 2.2],
        [0.5, 3],
        [0.9, 2.9],
        [1.43, 3.7],
        [1.6, 2.6],
        [1.7, 1.1],
        [1.9, 3.8],
        [2.1, 2.6],
        [2.28, 3.6],
        [2.38, 1.4],
    ])
    yy = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1])
    return xx, yy
def draw(xx, yy):
    plt.scatter(xx[:10, 0], xx[:10, 1], c='r', marker="^")
    plt.scatter(xx[10:, 0], xx[10:, 1], c='b', marker="*")
    plt.show()

if __name__ == "__main__":
    x, y = load_data()
    logistic = LogisticRegression()
    logistic.fit(x, y)
    print("k:{},b:{}".format(logistic.coef_, logistic.intercept_))
    # 画出回归线
    k1 = logistic.coef_[0, 0]
    k2 = logistic.coef_[0, 1]
    b = logistic.intercept_
    xx = np.arange(0, 2.5, 0.05)
    yy = (0 - b - k1*xx)/k2
    plt.scatter(xx, yy, c='g')

    x_test = np.array([[1.25, 2.0]])
    pre = logistic.predict(x_test)
    print(pre)
    plt.scatter(x_test[0, 0], x_test[0, 1], c='y', marker="s")
    draw(x, y)