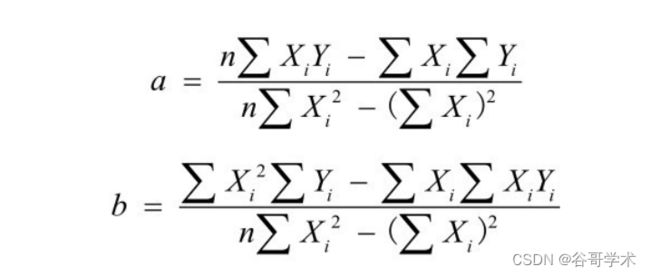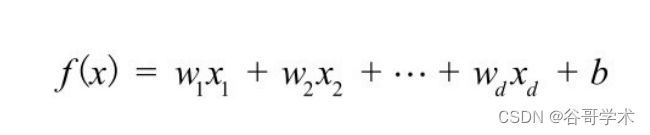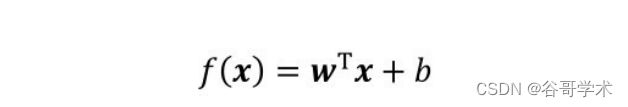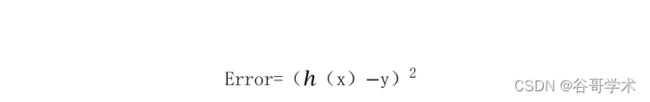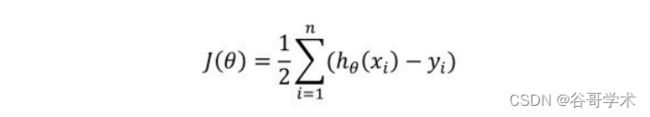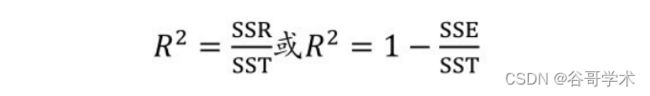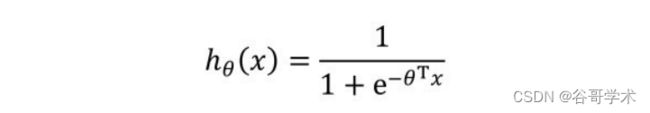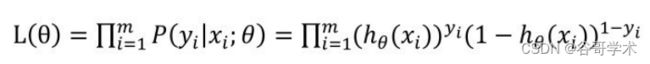人工智能知识全面讲解:回归分析
回归分析对我们来说并不陌生,早在小学的时候,有一种题目是从数列中
找规律,然后填出?一个数字。例如一个数列为“1、4、7、10、__”,请找
出规律填出?一个数字。对于这个简单的数列很容易看出规律,每一个后面的
数字是前一个加“3”得到的,因此横线处应该填写 13。实际上我们已经找到
了这个数列的函数表达式,也预测出了?一个值,只是我们当时只知道用“加
3”这样的方式表示。
在统计学中,回归分析法指利用数据统计原理,对大量统计数据进行数学
处理,确定因变量与某些自变量的相关关系,建立一个强相关性的回归方程
(函数表达式),并加以应用,来预测今后的因变量的变化的分析方法。简单
来说,可以把回归分析理解为研究不同变量相关关系的算法。例如在坐标轴中
随意画一条直线,这条直线反映了自变量x和因变量y之间关系,回归分析就是
用特殊的方法找到这个关系的算法。
回归分析按照涉及变量的多少,可分为一元回归分析和多元回归分析;按
照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量
之间的关系类型,可分为线性回归分析和非线性回归分析。按照不同维度,回
归分析有不同的类别。
回归分析中最常见的算法是线性回归以及逻辑回归,线性回归常用于处理
回归任务,输入的训练数据是连续型的数据,例如人体的身高、体重等属性;
逻辑回归常用于处理分类任务,输入的训练数据是离散型的数据,例如人体头
发的颜色、瞳孔的颜色等属性。这两个都是最常见的回归算法,产品经理必须
清楚两者的区别,重点掌握回归分析的实现原理以及所用数据的特点。实际上
回归分析模型并不难理解,但是在实际工作中,很多产品经理往往理不清头
绪,特征变量从哪来?又怎么选?模型的输出结果是什么?如何评价模型好
坏?有了模型如何应用等等一系列问题都出来了。希望你通过以?对回归分析
的学习,掌握回归分析的方法,从而在工作中更加得心应手。
4.2 线性回归
4.2.1 一元线性回归
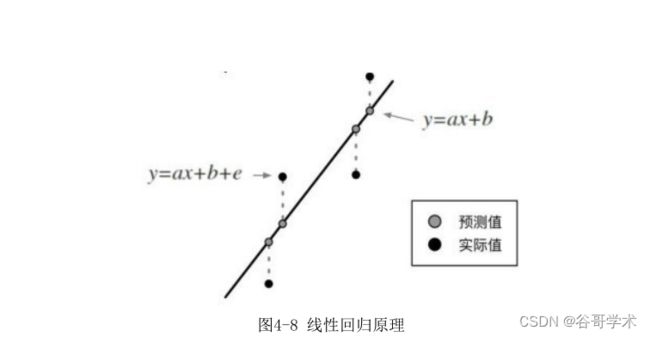
线性回归描述两个及以上变量之间的关系,最简单的一元线性回归则描述
两个变量之间的关系。回想初中的数学课堂上,老师教会我们如何求解一元一
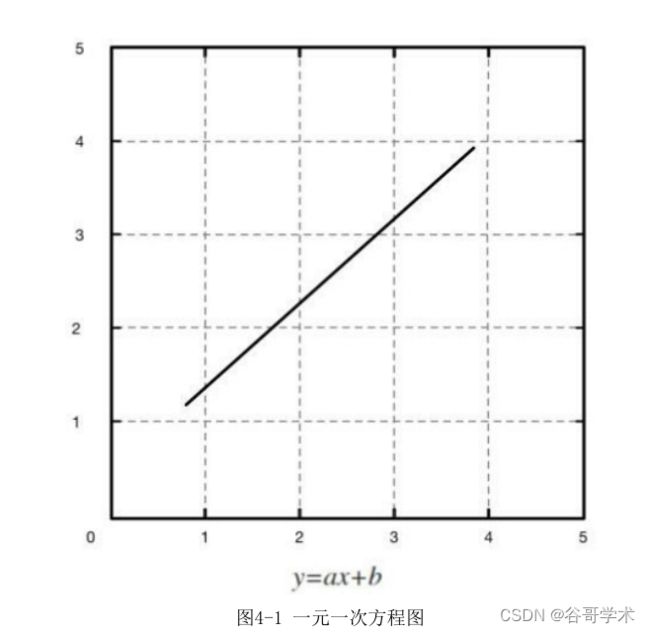
次方程,这是最简单的线性方程表达式。如图4-1所示,只需要知道坐标系上
任意两个点,通过解方程,就能求出一条穿过这两个点的直线,表达式为:
y=ax+b
一元一次方程的特点是,自变量x变化时,因变量y会随之改变,y的取值
只取决于x的变化。
在生活中我们也经常遇到这种场景,通过已知的一些数据,找到一个函
数,并预测?一个增长点出现的位置。例如某车间生产过程中,设备的折损率
与订单数量成正比,订单数量越多,机器运转的时间越长,设备出问题的概率
越高。因此我们通过以往订单数量与折损率之间的关系,找到一个函数表达
式,推测订单数量的峰值。如果超过这个峰值,那么设备损坏的概率极高,得
不偿失。由此我们可以将订单数量与机器折损率控制在一个平衡的状态中。
某企业在经营过程中,每个季度的销售额与广告的投放量成正比。广告投
放越多,越多客户知道该企业的产品,购买的人数也会越多。因此我们通过以
往每个季度的销售额与广告投放量之间的关系,预测?一个季度如果想达到一
定的销售额,需要投入多少广告成本;以及经济学家根据一段时间内的股票指
数变化预测后续股市的交易趋势是上升还是?降,等等,这些都是典型的一元
线性回归场景。
通过以上的例子可以看出,一元线性回归是分析只有一个自变量的线性相
关关系的方法。一个变量往往受许多因素的影响,若其中只有一个因素是主要
的,起决定性作用,则可用一元线性回归进行预测分析。我们用一个简单的例
子来探究一元线性回归的拟合过程。
某运动记录软件近期新增商城板块,用户可以在商城中购买运动装备。运
营一段时间后,负责这个模块的产品经理发现,经常运动的用户似乎更愿意在
商城中消费,消费的总金额也随运动总时长而增长。于是他想找到运动时长与
消费金额之间的规律,以便使用户的运动时长增加,从而使用户的购买率增
加。
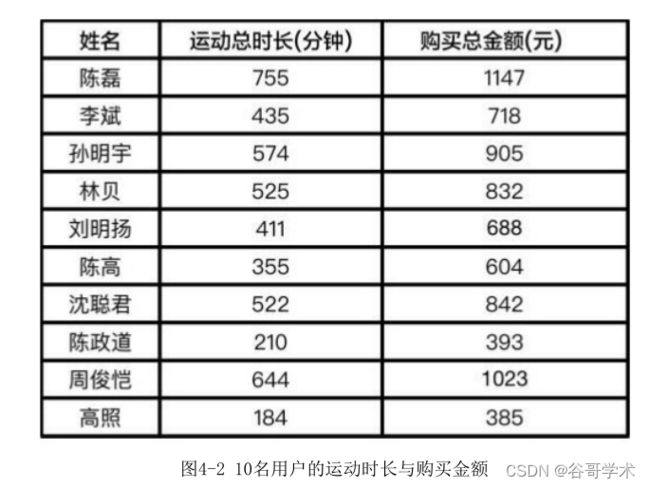
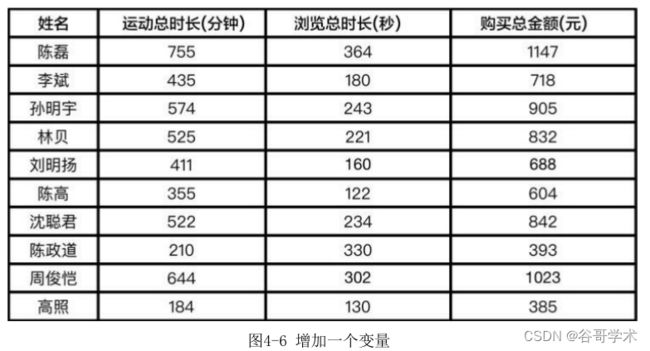
首先取10名用户的运动总时长与商场购买总金额,如图4-2所示。
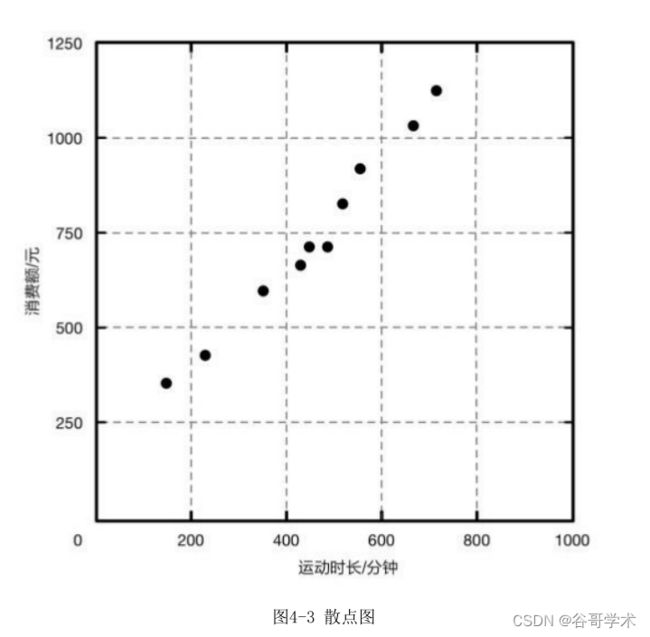
我们以用户的运动总时长作为x轴,消费总金额作为y轴,将这些数据表示
在平面直角坐标系中,能够得到一个散点图,如图4-3所示。
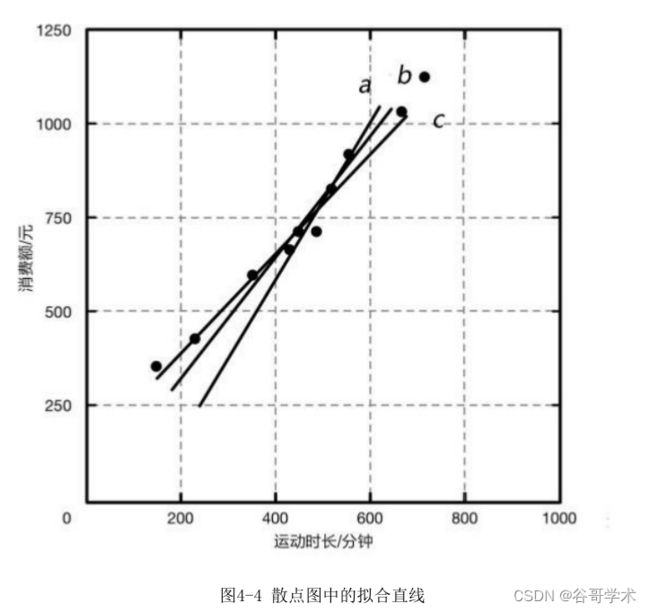
从这个散点图可以看出,如果想在这堆散点中用一条直线拟合这些数据
点,可以画出很多条直线,如图4-4所示。
图中的直线都可以用表达式y=ax+b表示,但是在表达式中,参数a和b的取
值如何确定?也就是说到?哪一条直线才是我们想要的方程呢?如何评判我们
挑选的直线就是最合适的直线呢?
还记得我们在第1章曾讲过,训练模型的过程从本质上来说,就是通过一
堆训练数据找到一个与理想函数最接近的函数。设想在最理想的情况?,对于
任何适合使用机器学习去解决的问题,在理论上都存在一个最优的函数能够完
美解决这个问题。但在现实应用中不一定能这么准确地找到这个函数,所以我
们找与这个理想函数接近的函数,如果其能够满足我们的使用那么我们就认为
它是一个好的函数。
回到这个场景中,模型找到与理想函数最接近函数的过程,实际上就是我
们通过这些数据点找到最佳的一元线性回归方程的过程。最佳的一元线性方程
按照我们的理解,就是能够完美穿过所有点的直线,每一个样本点都“恰
好”在这条线上。但是从图可以看出,实际上我们找不出这样的直线,恰好
穿过所有的样本点,所以只能找到最接近理想直线的直线,即这条直线尽量
靠近所有的样本点 。
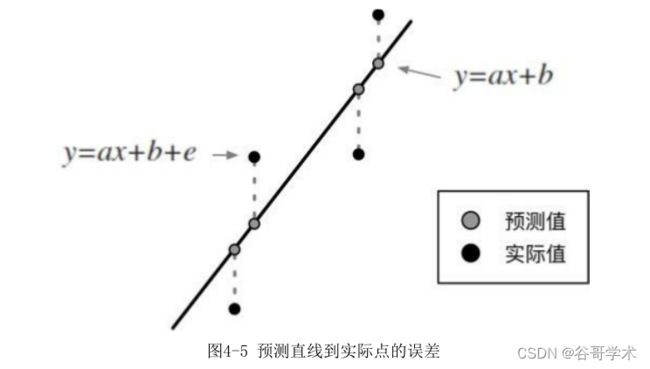
图中的数据点称为样本点,我们预测的直线上的点称为预测点,让这条直
线尽量靠近所有数据点,也就是让预测点距离样本点的误差尽可能小,如图4-
5所示。
为了计算预测点到样本点之间的误差,我们需要在算式中加入参数e代表
误差,用公式表示为:
y=ax+b+e
现在的解决思路转变为,寻找最理想函数的过程实际上是寻找让总误差最
小的方程,因此我们做一个移项,把每个点的误差表示为:
|e|=|y−ax−b|
只需要想办法利用已知的样本点(x,y)来寻找合适的参数a和b,使得误
差|e|的和对于所有已知点来说最小,我们就能够解决线性回归的问题。|e|的
和被称为?差和,可以表示为:
最后求?差和的最小值,我们一般通过“最小二乘估计”法推导出参数 a
和 b的求解公式,从而算出?差和。
在此简单讲解一?什么是“最小二乘估计”法,最小二乘估计法涉及较多
简单的数学知识。首先我们知道一元函数最小值点的导数为0,例如函数y=x 2
,式中x 2 的导数为2x。接?来我们令2x=0,求得x=0的时候,y取最小值。
实际上二元函数和一元函数比较类似。我们不妨把二元函数的图像设想成
一个曲面,把最小值想象成一个凹陷的位置,在这个凹陷?部,从任意方向上
看,偏导数都是0。因此,对于函数Q,分别对a和b求偏导数,然后令偏导数等
于0,可以得到一个关于a和b的二元方程组,由此可以求出a和b的具体取值,
这个方法被称为最小二乘法。
推导过程我们不展开?述。通过最小二乘估计法,我们可以得到a和b的求
解公式为:
有了这个公式,若想知道运动时长与商城购买金额之间的关系,我们可以
通过数据算出那条拟合直线,分别求出公式中的各种平均数,然后代入即可。
最后算出a=1.98, b=2.25,即最终的回归拟合直线为:
y=1.98x+2.25
利用这条回归直线,产品经理可以设置一些提高销售额的目标。例如要让
商城的销售额达到人均620元,那么整体运动时长必须提升到350分钟以上。当
用户运动到一定时长,我们可以增加一些激励措施或者设计一些小功能让用户
继续运动,提升用户的运动时长,这也是提升用户购买欲望的潜在方法。
4.2.2 多元线性回归
在回归分析中,如果有两个或两个以上的自变量,就称为多元回归。在实
际生活中,出现某种现象一定是与多个因素相关的,因此由多个自变量的组合
共同预测因变量,会比只用一个自变量进行预测更准确。因此多元回归的实际
意?更大。一元线性回归研究的是一个变量与结果之间的关系,而多元线性回
归研究的是多个变量与结果之间的关系。用公式表示为:
上式是一个多元一次线性方程,一般使用向量形式简写成:
其中w = (w 1 ,w 2 ,…,w d ),w和b就是模型需要学习的参数。
在上面的例子中,我们探究的是用户的运动时长与购买力之间的关系。随
着进一步的挖掘,产品经理又发现除了运动时长以外,用户在商城的平均浏览
时长也会对销售额产生影响,从数据上看,平均浏览时长越长的用户,消费的
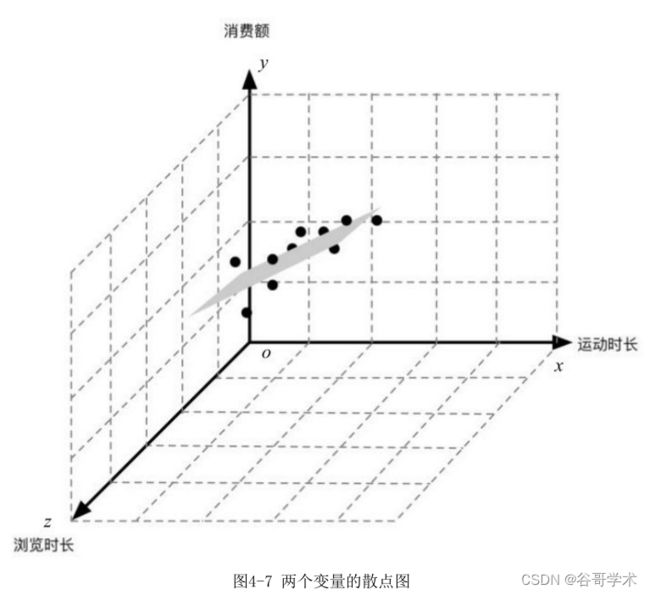
金额越大。于是我们找到这10个用户的商城平均浏览时长,如图4-6所示。这
一次我们研究两个自变量与一个因变量之间的关系,希望能够找出这两个变量
对销售额的影响。
增加一个变量以后,原本表示两个变量关系的二维平面变成了表示三个变
量关系的三维立面,如图 4-7 所示。如果增加更多的变量,则表示的图像维
度会不断升高,变成高维空间。超过三维后我们很难将其图像画出来。
从图中可以看出,实际上多元线性回归与一元线性回归的原理是相同的,
也是希望找到一个函数能够穿过所有的样本点,在三维空间中就是找到一个平
面,使所有的样本点恰好都落在这个平面上。但是实际上并不存在这样的平
面。因此,与一元回归模型一样,我们需要找到一个离所有点最“接近”的平
面。
值得注意的是,我们说线性回归的学习目标是要找到最优的参数w和b ,
以此确定一个超平面(直线与平面都是超平面),使得所有样本点到超平面
最“接近”,也就是距离最小。那么怎么来定?这里所说的“远近”关系呢?
在三维空间不像在二维平面那样好计算点到直线的距离,因此在回归问题中,
我们常用均方误差(Mean Squared Error)来表示样本点到这个超平面的远近
程度。均方误差的定?为:对于任意样本 (x,y) 和模型的预测值 h(x) ,均
方误差为标注值 y 和预测值 h(x)之间差的平方,用公式表示为:
因此,我们的目标变成了,使得训练数据中 N 个样本点的平均均方误差
最小。即令以?式子的值最小:
这个式子称为线性回归的损失函数。损失函数是回归模型中非常重要的概
念,它定?了模型效果的好与坏的评判标准。求得最优参数 w ,实际上就是
让 w 的损失值最小。对于多元线性回归方程,可以采用“最小二乘估计
法”或“梯度?降法”求解,具体的求解过程在此不展开?述。
在实际项目中,并非所有场景都适合做回归分析,明确问题的分析目标很
关键。获得样本数据以后,通常先从直方图、散点图入手,寻找数据之间因变
量和自变量可能存在的关系。只有当因变量与自变量确实存在某种线性关系
时,建立回归方程才有意?。因此作为自变量的因素与作为因变量的预测对象
是否有关,相关程度如何,以及判断这种相关程度的把握性多大,都是进行回
归分析必须要解决的问题。
在互联网领域,产品的运营数据无疑是一座待开垦的金矿。而机器学习模
型则是强有力的挖掘工具,帮助我们找出数据规律。回归分析模型是产品经理
手上一把强力的钻头,帮助其预测目标的趋势发展。例如上线某营销活动以
后,预估流量转化的销售额有多少;分析客户购买了某产品后,多长时间后会
再次购买新产品;预测某产品在未来半年内日活、月活用户数的增长趋势,等
等。以上例子都是对某些变量进行分析与运算,以此得到目标值变化趋势的典
型场景。
回归分析不但能够帮助我们预测发展趋势,制定业务运营的目标,也可以
用来寻找发生某些现象的原因,找到影响因变量的自变量有哪些。例如影响用
户购买某产品的原因、浏览某页面的时长的因素、用户点击购买的因素,等
等。只有带着数据需求,深入业务流程中,才能做到透过现象看本质,并且做
出理性的决策。
。
4.3 如何评价回归模型的效果
现在我们知道,在任何场景?都不存在一个“理想函数”,恰好拟合所有
样本点的数值,所以我们求得的只是一个最接近“理想函数”的拟合函数。无
论函数拟合得多好,肯定存在某些样本点没有落在该函数所表示的超平面上的
情况。因此需要通过一些指标定?函数的“拟合程度”,这也是判断模型效果
的关键。
回归分析来源于统计学,因此我们可以使用统计学的相关指标来评价拟合
程度。统计学中常用判定系数(coe??icient o? determination)R 2 判断回
归方程的拟合程度, R 2 越大,代表回归方程拟合程度越好;R 2 越小,代表回
归方程拟合程度越差。统计学认为,样本之所以存在波动,是函数的作用与
非函数的作用共同造成的。因此我 们需要使用三个不同的参数表示样本之间
的波动、函数的作用以及非函数的作用 。所以R 2 一般由以?三个参数组成。
(1)总偏差平方和(Sum o? Squares ?or Total,SST):是指每个因变
量y的实际值与因变量平均值Y(给定样本点的所有y的平均)的差的平方和,
这个指标反映了样本值的总体波动情况。总偏差平方和的计算公式为:
总偏差平方和=回归平方和+?差平方和
(2)回归平方和(Sum o? Squares ?or Regression,SSR):是指因变
量y的回归值(函数上的Y值)与其均值(给定样本点的Y值平均)的差的平方
和,它是由于自变量x的变化引起的y的变化,反映了因变量y的总偏差中由于x
与y之间的线性关系引起的y的变化部分,这个变化可以由回归函数解释,它体
现了函数的作用。
(3)?差平方和(Sum o? Squares?or Error,SSE):为了明确解释变
量和随机误差各产生的效应是多少,在统计学上把实际点与它在回归直线上预
测点相应位置的差异称为?差,把每个?差的平方加起来称为?差平方和,它
表示随机误差的效应。这个指标反映了除因变量对自变量的线性影响之外的其
他因素对样本产生变化的作用,这个变化不能用回归函数解释,它体现了非函
数的作用。
这三个参数怎么理解呢?还是以用户购买力与运动时长之间的关系为例。
实际上运动时长只是影响用户购买力的众多因素中一个相对比较重要的因素,
用户的购买力可能还受到用户的运动次数、商城的浏览时长、商品自身的吸引
力等众多难以把控的因素所影响。因此用户购买力是众多因素相互作用的最终
结果。由于每个用户在商城的消费金额是波动的,因此我们用每个用户的实际
消费金额与整体用户消费金额的平均值之间差的平方和来表示整体的波动情
况,即SST。
用回归模型拟合的函数只表示运动时长这个变量对于用户消费金额的影
响,因为还有其他的影响因素,所以实际值和预测值之间有所偏差,这也是
部分样本点没有落在函数拟合出来的平面上的根本原因 。因此我们说回归函
数只能解释一部分影响用户购买力的因素。实际值与预测值之间的差异,就是
除了运动时长之外其他因素共同作用的结果,是不能用回归函数解释的部分。
因此我们可以得到如?计算公式:
SST=SSR(回归函数可以解释的偏差)+SSE(回归函数不能解释的偏差)
对以上三个概念有了一个初步认识以后,我们再看R 2 的计算公式:
R 2 的取值在[0,1]之间,取值越接近1说明预测函数的拟合程度越好。假
设所有的样本点都在回归函数上,则SSE为0,R 2 =1,这意味着Y的变化完全是
由因变量的变化引起的,没有其他因素会影响样本的真实值,回归函数完全能
够解释样本的变化。如果R 2 很低,则说明X和Y之间可能不存在任何关系。
在产品工作中,经常遇到价值量化的问题。比如一些 B 端产品是为中小
企业服务的,上线新功能后如何评价这个功能的价值是一个颇具争议的问题。
如果单纯看点击率或使用率可能反映不了价值,只有销售额的变化最能够体现
出新功能的价值。但是企业的销售额有周期性的变化并且变化也不是由这个新
功能单独一个变量引起的,所以、我们就很难去量化新功能的价值。学习了判
定系数后,我们可以预测提升的产能与实际产能之间的偏差,尝试自己定义
判定系数的计算方式,来量化新功能带来的业务价值 。
4.4 逻辑回归
4.4.1 从线性到非线性
逻辑回归(Logistic Regression,LR)与线性回归一样,是一种应用广
泛的机器学习算法。该算法简单高效,预测速度快,而且容易学习和理解。逻
辑回归不仅适用于回归问题,也可以用于分类问题,通常我们用于解决分类问
题。实际上,逻辑回归仅仅是在线性回归的基础上,套用了一个逻辑函数。但
也是因为这个逻辑函数,使得回归模型在分类任务中大显身手,有了更为广阔
的应用前景,例如在流行病判别、个人信用评估以及计算广告学等很多领域都
能见到逻辑回归的身影。
在讲述逻辑回归的原理之前,我们先回顾线性回归的原理。通过以上的讲
解我们知道,线性回归的关键点是,对于多维空间中存在的样本点,可以用特
征的线性组合去拟合空间中点的分布和轨迹,如图4-8所示。
这时我们会思考,线性回归能够对连续值进行预测,那么也能够适用分类
场景吗?既然线性回归能够拟合出预测值的分布轨迹,即如果我们增加一个阈
值,把低于阈值的结果设为0,把高于阈值的结果设为1,不就可以解决最简单
的二分类问题了吗?
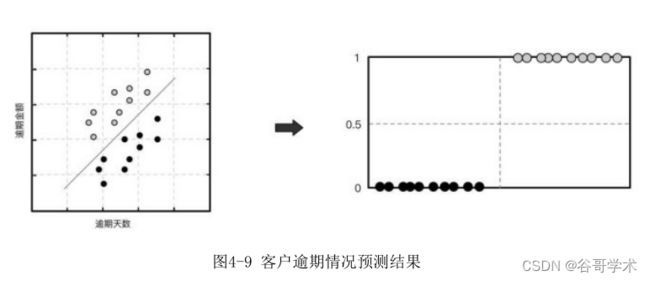
我们通过一个例子讲述这个问题。某信用卡中心试图通过以往客户的逾期
还款数据建立一个模型来判断新客户是否会出现恶意逾期的情况。如图4-9所
示,图中横坐标轴表示过往客户的逾期天数,纵坐标轴表示过往客户的欠款金
额,且黑色样本为非恶意逾期客户,灰色样本为恶意逾期客户。构建线性回归
模型后,我们设定阈值为0.5,模型判定h θ (x)≥0.5的客户为恶意逾期的客
户,而h θ (x)<0.5的客户为非恶意逾期客户。
如果数据分布像图 4.9 一样规整,那么我们用前文讲述的方法就可以解
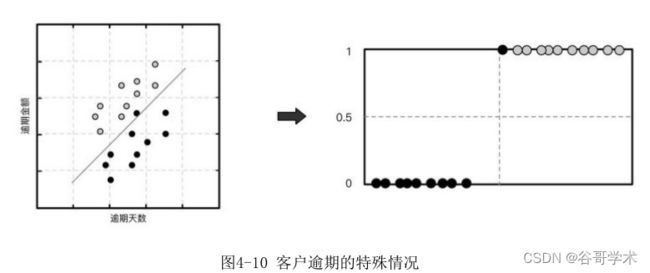
决问题。但在实际情况中,我们拿到的样本数据并没有这么准确,有一些客户
可能是超过了几天忘记还款,并非真的恶意逾期,如果用原来的方法判断会出
现如图 4-10 所示的情况。
这时如果我们还是用0.5的阈值,那么判定为恶意逾期的结果中就包含了
非恶意逾期的情况,判定结果显得没那么准确。如果出现更多逾期非恶意欠款
的情况,模型就更加难以应对。显然在线性回归中加入阈值的方法已经不能够
满足我们的分类需求。
细想到?是哪个环节出了问题。对于一个新输入的样本点,通过模型计算
出来的结果只要是大于0.5,哪怕只比0.5大了0.0001就会被分类为恶意逾期。
这个函数在0.5处有一个跃阶的现象,导致模型过于“敏感”,如图4-11所
示。
有没有什么方法可以让这个函数表现更“光滑”一点,变得不那么敏感
呢?
生活中很多事情并不是非黑即白,所谓的对和错并没有那么绝对。现在我
们遇到的情况就是模型太过于“死板”,出来的结果非负即正。要想解决这个
问题,可以尝试将直接判断结果是正是负转化为判断结果是正类或负类的概率
是多少。原本的方法在阈值大于0.5的情况?就直接判定为正类,现在改变为
不直接判定类别,只输出是正类或负类的概率是多大,概率越高,判定的把握
越大,是正类的可能性也就越高。有了这个思路以后,我们需要找到从输出某
个结果转化为输出某个结果的概率的方法。
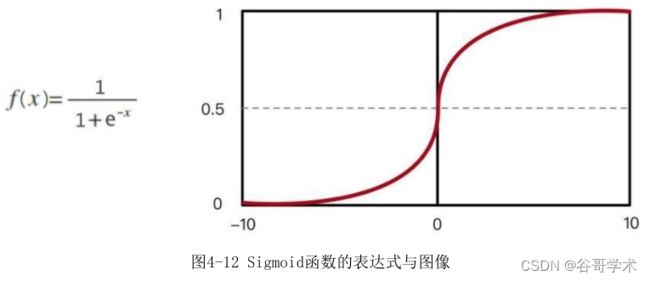
4.4.2 引入Sigmoid函数
有了解决思路,还需要找到具体的实现方法。在数学上恰好存在Sigmoid
函数具有这样的特性,其能够满足我们的需要。这个函数的输入范围是
−∞→+∞,而值域则光滑地分布在0到1之间。函数表达式和图像如图4-12所
示。
从函数图像上看,函数y=g(z)在z=0的时候取值为0.5。随着z逐渐变小,
函数值趋于 0。z 逐渐变大时,函数值逐渐趋于 1,这正好是一个概率的表达
范围。由此我们可以得到逻辑回归算法的公式为:
逻辑回归的本质是线性回归。只是在特征转变为输出结果的时候,加入了
一层函数映射,即先把特征线性求和,然后使用函数g(z)作为假设函数进行预
测。我们看到的参数z实际上是一个线性回归方程,只不过在这里用符号表
示。逻辑回归的求解方式与线性回归相同,都是通过损失函数的方式?近最优
解求得结果。
逻辑回归的目的不仅仅是将样本分成0或1两类,更重要的是样本分类的准
确性。例如进行肿瘤检测时,在患者确诊带有肿瘤的情况?,我们更关心患恶
性肿瘤的概率是多少。因此对于逻辑回归,我们可以理解它通过概率将样本分
成了0和1两类。由于逻辑回归的这个特性,在互联网领域我们通常使用逻辑回
归预测客户流失的概率、客户恶意欠款概率以及进行风险监测。
因为逻辑回归不是通过一个固定的阈值判定样本数据的正负性,所以在二
维平面上也不再是简单的一刀切,通过一条直线区分不同类别的样本。逻辑回
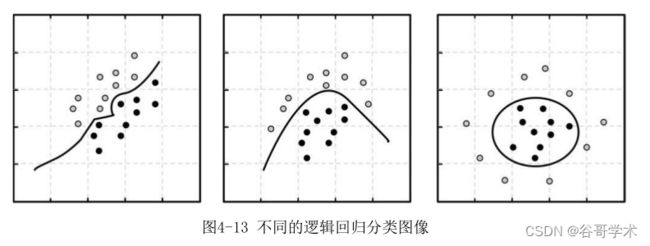
归更具有包容性,可以将不能线性区分的数据集区分开。这一切归因于激活函
数Sigmoid,其将因变量与自变量之间的线性关系变成了非线性关系,使得函
数在二维平面上的表现更为柔和,也就是说分类的判定边界变得更加贴合样本
数据的特点,如图4-13所示。
以上三幅图中的实心圆与空心圆样本点为不同的类别。使用逻辑回归生成
的分类边界,不管是直线或曲线,都能够将图中的两类样本点区分开。?面我
们来看看,逻辑回归是如何根据样本点获得这些判定边界的。
生成判定边界与 h θ (x)的取值有很大关系。只要 h θ (x)设计得足够合
理,我们就能在不同的样本分布环境?,拟合出不同的判定边界,从而把不同
类别的样本点区分开。接?来的问题就变成如何获得最合适的参数h θ (x),如
何计算参数h θ (x)的具体取值。
逻辑回归与线性回归相同,我们没有办法找到一个完美的函数完全拟合预
测类别的概率,只能想办法找到一个最接近理想函数的函数。因此我们的解决
思路是让h θ (x)的计算值与理想值之间的损失最小,也就是引入一个损失函
数。
最合适的参数ℎ θ (x),其实就是让损失最小的h θ (x)。说到损失函
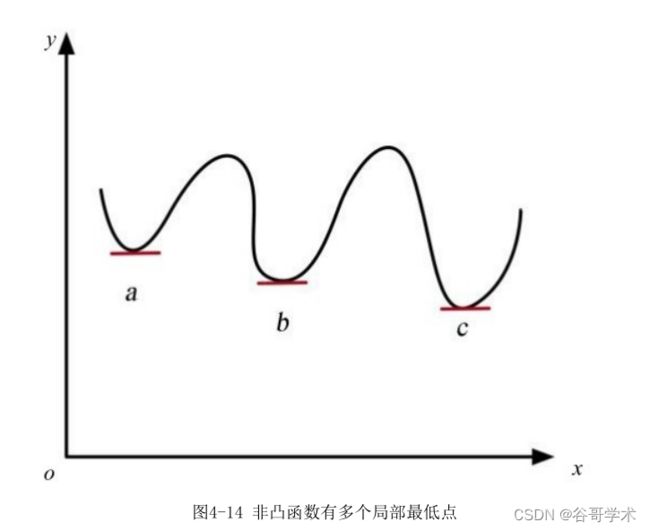
数,我们首先想到的是线性回归模型中使用的均方误差。使用均方误差作为损
失函数可以求解,但是会导致损失函数变成一个“非凸”函数,简单地说就是
这个函数有很多个局部最低点,如图4-14所示。
如果出现图 4-14 这种情况,我们很难把握到?在什么时候损失函数才达
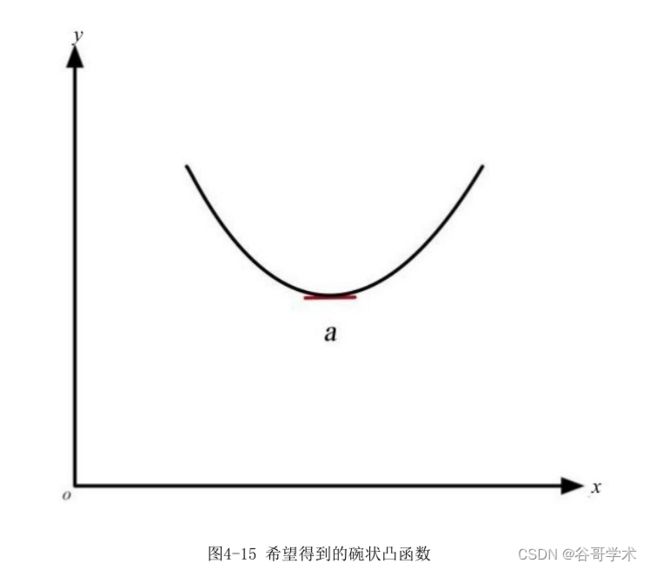
到了全局最小值。最理想的情况是找到一个“碗状结构”的凸函数作为损失函
数,这样我们通过求解得到的局部最低点一定是全局最小值点,如图4-15所
示。
十分幸运的是,在数学上恰好有一种方法可以构造这个碗状结构的凸函
数,即采用“最大似然估计法”建立损失函数。使用最大似然估计法推导损失
函数的过程比较繁杂,在这里不再展开?述。我们只需要了解通过最大似然估
计法,获得的损失函数的表达式为:
构造出符合我们要求的碗状结构凸函数以后,问题还没结束。我们的目标
是找到这个凸函数的最低点,那么如何才能找到这个函数的最低点呢?