浅谈深搜广搜
深搜广搜
-
- 深度优先搜索 Depth First Search(DFS)
-
- 简介:
- 基本思想:
- 回溯法:
- 深搜优缺点
-
- 优点
- 缺点
- 分析
- 算法的实际实现流程:
- 算法举例
-
- 例一:
- 例二:
- 广度优先搜索 Breadth First Search(BFS)
-
- 简介:
- 基本思想:
- 广搜优缺点:
-
- 优点
- 缺点
- 分析
- 算法的实际实现流程:
- 算法举例:
-
- 例一:
- 例二:
- 例三:
深度优先搜索 Depth First Search(DFS)
简介:
- 深度优先搜索所遵循的搜索策略是尽可能深地搜索树,属于盲目搜索。
基本思想:
- 为了求得问题的解,会将每一结点所有可能路径都走一遍,先选择某一种可能情况向前(子结点)探索,在探索过程中,一旦发现原来的选择不符合要求,就回溯至父亲结点(可认为是上一结点)重新选择另一结点,继续向前探索,如此反复进行,直至求得最优解。深度优先搜索的实现方式可以采用递归或者栈来实现。(深搜会找出所有解)
回溯法:
- 回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法
深搜优缺点
优点
- 能找出所有解决方案
- 优先搜索一棵子树,然后是另一棵,所以和广搜对比,有着内存需要相对较少的优点
缺点
- 要多次遍历,搜索所有可能路径,标识做了之后还要取消(视情况为认定)。
- 在深度很大的情况下效率不高
分析

例子1:找到从a到h的路线
分析:遍历优先级:上优先于下结点
回溯的实现是由for循环和函数递归嵌套实现的
- 回溯完成将在存在多条分路结点产生
从a出发,开始深搜,下一可能路径为B, C, D,进入B结点,B结点下一可能路径为E,进入E结点,E结点下一可能路径为G,进入G结点,G结点不是目标结点且无路可走开始回溯,后退一步进入E结点,E结点无另外路径,再次后退一步进入B结点,同理,再次后退,进入A结点, A结点除B外还存在C, D,回溯完成,再次进行搜索,进入C结点,C结点可进入E结点,E结点下一可能路径为G,进入G结点,G结点无路可走开始回溯,后退一步进入E结点,E结点无另外路径,再次后退一步进入C结点,C结点除E结点外存在F结点,回溯完成,进入F结点,F进入G,再次回溯,回溯至F结点,回溯完成,进入H结点,DFS完成,路线为A->C->F->H,虽然此时已经找到路线但其仍会回溯至A,然后由A->D->H到达目标,再次回溯至A点,发现所有路径已走,退出最外层DFS,深搜结束
优化:从上述过程我们不难发现,在第二次从A搜索时,C结点仍走向了E结点,在第一轮搜索中已经走过此路径,发现从E结点无法走到目标地点,此时走向E结点是无用的,所以在深搜中我们需要标记已走过的路径,避免重复搜索(在有些情况下不进行标记将无法完成搜索),此时在第二轮从A搜索将直接从A->C->F->H,由于E点,G点已被标记将不再进入(此优化后将只产生一种路径,因为在到达一次目标点后,H点将被标记,后续将不能走到H点)
例子2:找到从a到h的路线最少走几步
分析:由于我们需要找到最短路径,所以需要找到所有能到达H点的路径,比较得到最小值,所以上面不优化深搜过程符合要求,只需定义min记录最步数,count统计步数,每次在走到H点时比较count和min,维护min一直未最小值,最终min为2
优化:我们其实对所走路径仍可进行标记,但由于我们需要所有可能路径,所以我们需要在对有些点的标记进行清除,我们将可到达H点的路径上的结点的标记进行清除,从而使后续仍能经过此路径
算法的实际实现流程:
- 先找到每一步能走的各种可能
- 寻找问题边界
- 想办法标记经过路径(有的需要消除标记)
- 写出DFS函数(递归函数)
- 遍历全图进行深搜
算法举例
例一:
岛屿数量:
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
示例 2:
输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出:3
m = grid.length
n = grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’
解题思路:遍历所有位置,如果当前为‘1’则将其修改为‘0’(表示此处已被经过),然后寻找上下左右四个方向,如果存在则重复此过程(深搜过程),当搜索完成,与之相连的‘1’都被修改为‘0’,定义count记录陆地数量,遍历判断每个元素,若是‘1’则count自增1,之后搜索与之相邻陆地,将其标记为‘0’,遍历完成返回count
代码实现:
int dir[4][2] = {{0,1}, {1,0}, {0,-1}, {-1,0}};//用二维数组表示四个方向
void dfs(char ** grid, int row, int col, int x, int y)
{
if(x < 0 || x >= row || y < 0 || y >= col || grid[x][y] == '0')//处理边界,是否为‘0’必须得放在最后一个,不然-1超出数组范围
return ;
else
grid[x][y] = '0';
for(int i = 0; i < 4; i++)
{
int xx = x + dir[i][0];
int yy = y + dir[i][1];
dfs(grid, row, col, xx, yy);
}
}
int numIslands(char** grid, int gridSize, int* gridColSize)//grindcolSize上传二维数组的列数
{
int col = gridColSize[0];/*列数gridColSize[0]可替换为*gridColSize,[0]表示读取此地址的int型数据,[1]表示读取此地址偏移一个sizeof(int)字节地址的int型数据, 所以在此处两者相等*/
int row = gridSize;//行数
int count = 0;
for(int i = 0; i < row; i++)
for(int j = 0; j < col; j++)//遍历每个点
{
if(grid[i][j] == '1')
{
dfs(grid, row, col, i, j);
count++;
}
}
return count;
}
以示例一为例分析流程:
dir[4][2] = {{0,1}, {1,0}, {-1,0}, {0,-1}} 决定搜索时优先进入的点,此dir表示顺序为右下左上

将其数组编号,并给数组外围增加一圈0,表示超范围(例如(0,0)点向左走,进入(0,-1)点,超出范围用0表示),将岛屿标为黄色,无色表示海
以(0,0)点即1点为起始点,开始深搜,(0,0)点有如下搜索路径

行走路线:1->2->3->4然后4走向5,5不符合要求,回溯至4重新选择,选择9,9无路可走开始回溯,回溯过程与4->5过程类似(选择可能路径),由于2存在可能路径,随意回溯至2,从2进入7,经过与第一次类似过程,最终退出最外层DFS,完成搜索
在深搜中由于每一次都进行标记,所以上所经过路径都被标记(即下次再经过时不在进行搜索),对于本示例,1点符合,进行第一轮搜索,count++,完成搜索,我们发现,数组全变为‘0’,然后遍历完所有位置,不在存在符合结点,此时count = 1,即只存在一块岛屿。
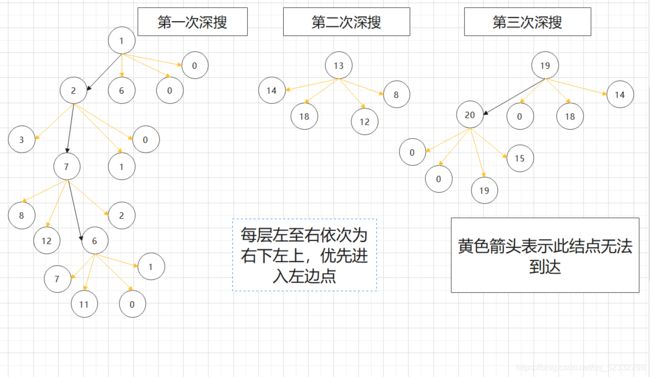
以示例二为例分析流程:
行走路线:
第一次深搜:1->2->7->6
第二次深搜:13
第三次深搜:19->20
1点符合要求,进行第一次深搜,将相邻符合点全部标记,完成搜索,count++;然后判断2点,不符合,判断3点,依次类推,13点符合,进行第二次深搜,count++;然后继续向后遍历,19点符合,进行第三次深搜,count++;继续遍历,直到遍历完所有位置,此时count = 3,即存在三块岛屿。
例二:
全排列问题:
列出所有数字1到数字n的连续自然数的排列,要求所产生的任一数字序列中不允许出现得复数字。
输入:
n (1<=n<=9)
示例一:
输入: 3
输出:
123
132
213
231
312
321
示例二:
输入: 4
输出:
1234
1243
1324
1342
1423
1432
2134
2143
2314
2341
2413
2431
3124
3142
3214
3241
3412
3421
4123
4132
4213
4231
4312
4321
**解题思路:**定义a[9]记录排列的数,定义book[9]用于标记排列过的数字,排列通过深搜时对数字的标记和消除实现对数字的重复使用,达到全排列的要求
#include以示例一为例分析流程:

123为运行的先后顺序,对比此题与上一题,我们不难发现,在上一题中一个树中每个结点都只能被使用一次,而此题,每个结点可被多次使用,因为在每一轮回溯时会对标记值进行清除
广度优先搜索 Breadth First Search(BFS)
简介:
BFS是一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
基本思想:
宽度优先搜索的核心思想是:从初始结点开始,应用算符生成第一层结点,检查目标结点是否在这些后继结点中,若没有,再用产生式规则将所有第一层的结点逐一扩展,得到第二层结点,并逐一检查第二层结点中是否包含目标结点。若没有,再用算符逐一扩展第二层所有结点……,如此依次扩展,直到发现目标结点为止(并不会找出所有解,到达目标点直接结束搜索),广度优先搜索同过while循环和队列实现。while循环判断条件为队列不为空,每次将头指针所指拿出用于下一层结点的扩展。
广搜优缺点:
优点
- 对于解决最短或最少问题特别有效,而且寻找深度小
- 每个结点只访问一遍,结点总是以最短路径被访问,所以第二次路径确定不会比第一次短
缺点
- 内存耗费量大(需要开大量的数组单元用来存储状态,用数组模拟队列)
分析
初始图:
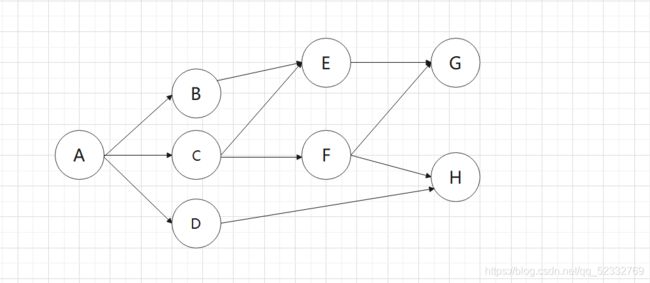
例子:找到从A到H的路线
初始化队列用来存储所走路径,绿色箭头表示头指针,红色箭头表示尾指针
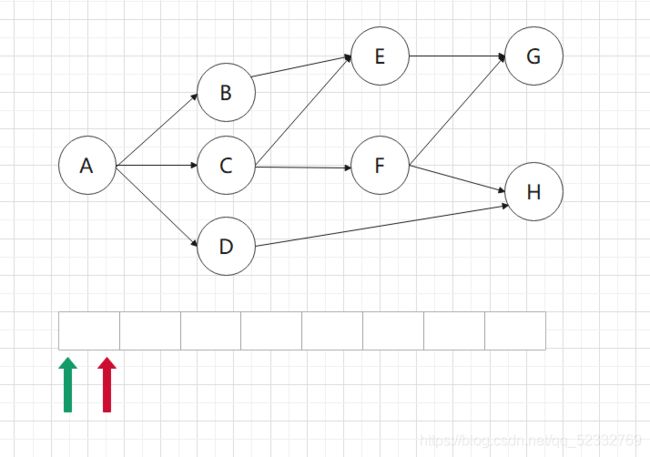
由于从A点出发,所以先将A点入队,此时状态为图1,然后将A点出队用于下层结点扩展,扩展完成状态为图2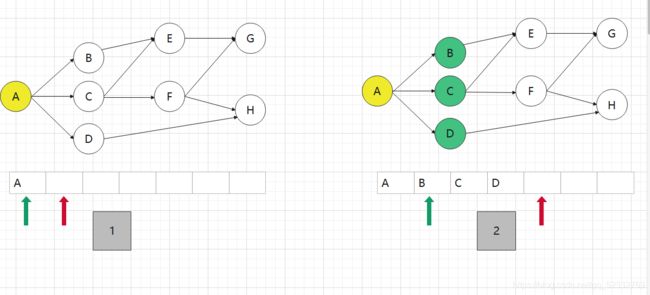
再将B点出队,用于下层扩展,扩展结果为图3,再将C点出队,用于下层扩展,扩展结果为图4,此时我们发现,C点可走向E点,但C的扩展结果并没有E点,因为再广搜时我们也会对所走路径进行标记,避免重复搜索(标记很重要)
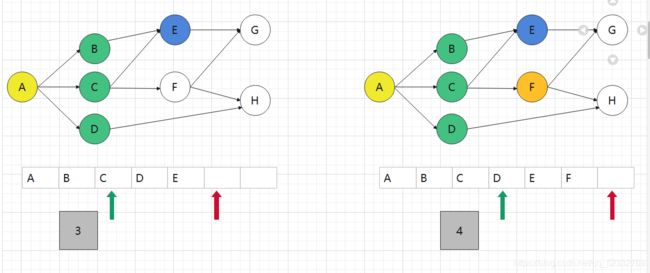
将D点出队,用于下层扩展,扩展结果为图5,此时发现扩展结点存在目标点H,广搜结束,所走路径为A->D->H

我们发现,上面过程在找到路径时正好就是最短路径,所以广搜一般被用于解决最短路径问题。
下面我们看一下无目标结点时如何退出搜索:
还是上初始图,我们将题改为:找到从A到K的路线
搜索过程前面一样,所以我们从扩展至图5时分析,此时H将不再是目标点,
所以继续搜索,将E点出队,用于下层扩展,扩展结果为图6
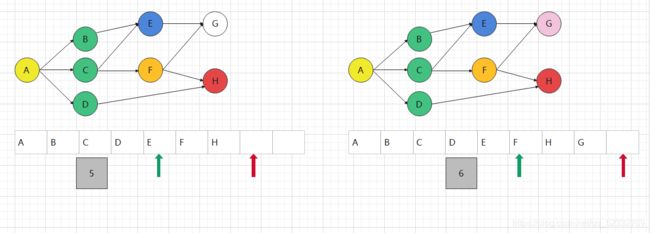
然后继续搜索,将F点出队,用于下层扩展,F并无新路径可走,所以此次扩展并无新元素入队,实现队列的所减,重复此过程,最终所有元素全部出队,结束广搜。
算法的实际实现流程:
- 先找到每一步能走的各种可能
- 寻找入队条件
- 想办法标记经过路径
- 循环搜索
算法举例:
例一:
岛屿数量:
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
示例 1:
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
示例 2:
输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出:3
m = grid.length
n = grid[i].length
1 <= m, n <= 300
grid[i][j] 的值为 ‘0’ 或 ‘1’
解题思路:(与深搜一样)遍历所有位置,如果当前为‘1’则将其修改为‘0’(表示此处已被经过)并入队,然后开始广搜,当搜索完成,与之相连的‘1’都被修改为‘0’,定义count记录陆地数量,遍历判断每个元素,若是‘1’则count自增1,之后搜索与之相邻陆地,将其标记为‘0’,遍历完成返回count。
代码实现:
//广度优先搜索:通过队列对数组进行遍历搜索
//定义count记录岛屿数量
/*遍历所有位置,若当前位置符合题意的位置入队,count++,
然后while循环对队列进行操作,记录队列头的位置判断它所能走到的所有位置,
将其入队,将能走的位置进行标记,避免重复操作,然后头指针指向出队,
判断下一位置,直到队列为空*/
int numIslands(char** grid, int gridSize, int* gridColSize){
int col = *gridColSize;
int cow = gridSize;
int queuex[1200];
int queuey[1200];
int count = 0, x, y;
for(int i = 0; i < cow; i++)
for(int j = 0; j < col; j++)
{
int left = 0, right = 0;
if(grid[i][j] == '1')
{
grid[i][j] = '0';
count++;
queuex[right] = i;
queuey[right] = j;
right++;
while(left < right)//
{
x = queuex[left];
y = queuey[left];
if(y+1 >= 0 && y+1 < col && grid[x][y+1] == '1')
{
grid[x][y+1] = '0';
queuex[right] = x;
queuey[right] = y + 1;
right++;
}
if(x+1 >= 0 && x+1 < cow && grid[x+1][y] == '1')
{
grid[x+1][y] = '0';
queuex[right] = x + 1;
queuey[right] = y;
right++;
}
if(y-1 >= 0 && y-1 < col && grid[x][y-1] == '1')
{
grid[x][y-1] = '0';
queuex[right] = x;
queuey[right] = y - 1;
right++;
}
if(x-1 >= 0 && x-1 < cow && grid[x-1][y] == '1')
{
grid[x-1][y] = '0';
queuex[right] = x - 1;
queuey[right] = y;
right++;
}
left++;
}
}
}
return count;
}
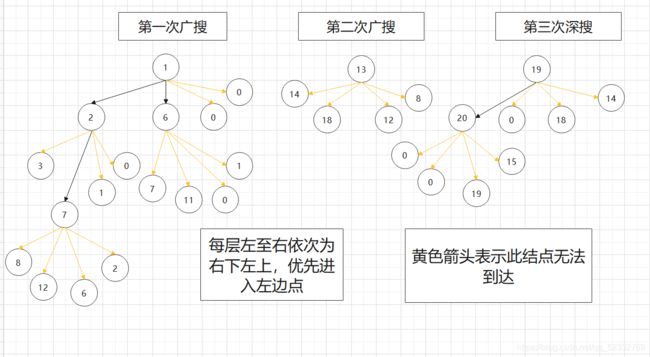
以示例一为例分析流程:
此搜索方向仍为右下左上,方向优先级由while内if顺序决定。
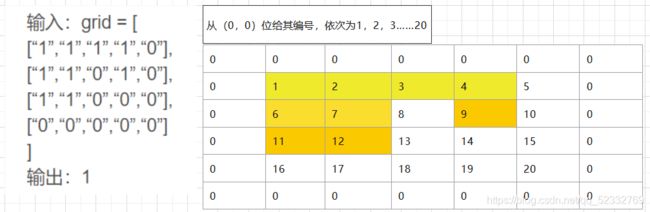
将其数组编号,并给数组外围增加一圈0,表示超范围(例如(0,0)点向左走,进入(0,-1)点,超出范围用0表示),将岛屿标为黄色,无色表示海
以(0,0)点即1点为起始点,开始广搜,(0,0)点有如下搜索路径
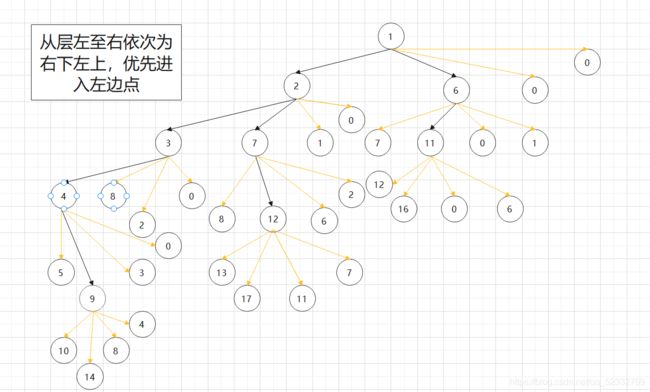
入队顺序为:1->2->6->3->7->11->4->12->9
对应所需步数为:0->1->1->2->2->2->3->3->4
对于本示例,1点符合,它会以上述路径完成入队,完成广搜,将岛屿标记为’0’;进行一轮搜索,count++,完成搜索,我们发现,数组全变为‘0’,然后遍历完所有位置,不在存在符合结点,此时count = 1,即只存在一块岛屿。
例二:
打开转盘锁(力扣752):
你有一个带有四个圆形拨轮的转盘锁。每个拨轮都有10个数字: '0', '1', '2', '3', '4', '5', '6', '7', '8', '9' 。每个拨轮可以自由旋转:例如把 '9' 变为 '0','0' 变为 '9' 。每次旋转都只能旋转一个拨轮的一位数字。
锁的初始数字为 '0000' ,一个代表四个拨轮的数字的字符串。
列表 deadends 包含了一组死亡数字,一旦拨轮的数字和列表里的任何一个元素相同,这个锁将会被永久锁定,无法再被旋转。
字符串 target 代表可以解锁的数字,你需要给出最小的旋转次数,如果无论如何不能解锁,返回 -1。
示例 1:
输入:deadends = ["0201","0101","0102","1212","2002"], target = "0202"
输出:6
解释:
可能的移动序列为 "0000" -> "1000" -> "1100" -> "1200" -> "1201" -> "1202" -> "0202"。
注意 "0000" -> "0001" -> "0002" -> "0102" -> "0202" 这样的序列是不能解锁的,
因为当拨动到 "0102" 时这个锁就会被锁定。
示例 2:
输入: deadends = ["8888"], target = "0009"
输出:1
解释:
把最后一位反向旋转一次即可 "0000" -> "0009"。
示例 3:
输入: deadends = ["8887","8889","8878","8898","8788","8988","7888","9888"], target = "8888"
输出:-1
解释:
无法旋转到目标数字且不被锁定。
示例 4:
输入: deadends = ["0000"], target = "8888"
输出:-1
提示:
- 死亡列表
deadends的长度范围为[1, 500]。 - 目标数字
target不会在deadends之中。 - 每个
deadends和target中的字符串的数字会在 10,000 个可能的情况'0000'到'9999'中产生。
//广度优先搜索
//change函数返回转盘锁拨动后的字符,1向上拨,-1向下拨
//定义book数组标记死亡列表,book数组初始化为0,将死亡字符串对应角码的book赋值为1,以达到死亡字符串的更新与标记
//定义字符类型二维数组queue用于广搜存储可经过路径,定义整型一维数组queuel存储步数
/*起始判断"0000"是否在死亡列表,在的话直接返回-1,然后判断是否为target字符串,是的话返回0(表示到达目标只需转动0次),
然后将"0000"入队成为起始位置,并更新死亡列表将"0000"加入,防止重复判断,queuel[0]赋值为0,表示0已走0步
*/
//每一位置都有八种可能路径,即每0一位上下拨动
/*从队列头开始判断,对其八种情况分别判断,若其与target相同则返回其对应queuel+1(加0以表示走到当前位置还需走一步),若其不在死亡队列,则将其入队,将其添加死亡队列(类似于岛屿问题的标记,若无此步骤,此轮上拨,在下轮下拨后将还原,陷入死循环),对应queuel更新,反之之则不入队(达成队列的缩减,以最后终止循环),*/
//若队列为空,仍无返回值则表示无法到达目标位置,返回-1
char change(char s, int i)//i为1表示向上拨,i为-1表示向下拨
{
if(s == '9' && i == 1)
return '0';
else if(s == '0' && i == -1)
return '9';
else
return s + i;
}
int openLock(char **deadends, int deadendsSize, char * target){
char queue[20000][5];//中间步骤
int queuel[20000];//步数队列
int left = 0, right = 0;
int book[10000] = {0};//标记数组,初始化为零
for(int i = 0; i < deadendsSize; i++)//添加死亡队列
book[atoi(deadends[i])] = 1;
if(book[0] == 1)//起始判断
return -1;
else if(!strcmp(target, "0000"))
return 0;
else
book[0] = 1;
for(int i = 0; i < 4; i++)//将起始位置入队
queue[0][i] = '0';
right++;
queuel[0] = 0;
while(left < right)//循环广搜
{
char s[5];
strcpy(s, queue[left]);
s[0] = change(s[0], 1);
if(book[atoi(s)] == 0)
{
if(!strcmp(s, target))
return queuel[left] + 1;
strcpy(queue[right], s);
book[atoi(s)] = 1;
queuel[right] = queuel[left] + 1;
right++;
}
strcpy(s, queue[left]);
s[0] = change(s[0], -1);
if(book[atoi(s)] == 0)
{
if(!strcmp(s, target))
return queuel[left] + 1;
strcpy(queue[right], s);
book[atoi(s)] = 1;
queuel[right] = queuel[left] + 1;
right++;
}
strcpy(s, queue[left]);
s[1] = change(s[1], 1);
if(book[atoi(s)] == 0)
{
if(!strcmp(s, target))
return queuel[left] + 1;
strcpy(queue[right], s);
book[atoi(s)] = 1;
queuel[right] = queuel[left] + 1;
right++;
}
strcpy(s, queue[left]);
s[1] = change(s[1], -1);
if(book[atoi(s)] == 0)
{
if(!strcmp(s, target))
return queuel[left] + 1;
strcpy(queue[right], s);
book[atoi(s)] = 1;
queuel[right] = queuel[left] + 1;
right++;
}
strcpy(s, queue[left]);
s[2] = change(s[2], 1);
if(book[atoi(s)] == 0)
{
if(!strcmp(s, target))
return queuel[left] + 1;
strcpy(queue[right], s);
book[atoi(s)] = 1;
queuel[right] = queuel[left] + 1;
right++;
}
strcpy(s, queue[left]);
s[2] = change(s[2], -1);
if(book[atoi(s)] == 0)
{
if(!strcmp(s, target))
return queuel[left] + 1;
strcpy(queue[right], s);
book[atoi(s)] = 1;
queuel[right] = queuel[left] + 1;
right++;
}
strcpy(s, queue[left]);
s[3] = change(s[3], 1);
if(book[atoi(s)] == 0)
{
if(!strcmp(s, target))
return queuel[left] + 1;
strcpy(queue[right], s);
book[atoi(s)] = 1;
queuel[right] = queuel[left] + 1;
right++;
}
strcpy(s, queue[left]);
s[3] = change(s[3], -1);
if(book[atoi(s)] == 0)
{
if(!strcmp(s, target))
return queuel[left] + 1;
strcpy(queue[right], s);
book[atoi(s)] = 1;
queuel[right] = queuel[left] + 1;
right++;
}
left++;
}
return -1;
}
例三:
完全平方数(力扣279):
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, ...)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
给你一个整数 n ,返回和为 n 的完全平方数的 最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12
输出:3
解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13
输出:2
解释:13 = 4 + 9
提示:
-
1 <= n <= 104//广度优先搜索 //定义队列queue记录可以路径,queuel记录与之对应的路径的步数 //定义book标记出现过的大小的可能方式,初始化为零,表示都没出现过,出现过的赋值为1 //当queue[left]+i*i小于目标值,然后判断其是否出现过(出现过的book[其]等于1),未出现过则入队,并将其book赋值1 //因为最大值为10000,所以每次增加的i*i中的i的范围为1到100 int numSquares(int n){ int queue[10000];//可能队列 int queuel[10000];//出现过的队列 int book[10000] = {0};//标记数组 int left = 0, right = 0;//初始化队列 if(n == 0)//若n为零则发明会零 return 0; queue[right++] = 0;//将起始位置入队 queuel[0] = 0; book[0] = 1; while(left < right) { for(int i = 1; i <= 100; i++) { if(queue[left] + i * i < n && book[queue[left] + i * i] == 0) { book[queue[left] + i * i] = 1; queue[right] = queue[left] + i * i; queuel[right] = queuel[left] + 1; right++; } else if(queue[left] + i * i == n) return queuel[left] + 1; } left++; } return 0; }