阿白数模笔记之岭回归（ridge regression）与LASSO回归（Least Absolute Selection and Shrinkage Operator）
目录
Preface
一、岭回归（Ridge regression）
①岭系数
②代价函数（Costfunction）
③参数矩阵的解
④岭系数的确定
Ⅰ、岭迹法
Ⅱ、迭代法
二、LASSO回归（Least Absolute Selection and Shrinkage Operator）
①代价函数
②惩罚系数的确定
③参数矩阵的解
Ⅰ、坐标下降法（Coordinate descent）
Ⅱ、最小角回归法（Least Angle Regression，LARS）
Preface
在阿白数模笔记之最小二乘法（Least square method）中提到过复共线性的问题，岭回归和LASSO回归是一种解决方式。岭回归(ridge regression, Tikhonov regularization)是一种专用于共线性数据分析的有偏估计回归方法，实质上是一种改良的最小二乘估计法，通过放弃最小二乘法的无偏性，以损失部分信息、降低精度为代价获得回归系数更为符合实际、更可靠的回归方法，对病态数据的拟合要强于最小二乘法。Lasso回归的全称是Least Absolute Selection and Shrinkage Operator，即最小绝对值选择与收缩算子。Lasso方法是以缩小变量集（降阶）为思想的压缩估计方法。它通过构造一个惩罚函数，可以将变量的系数进行压缩并使某些回归系数变为0，进而达到变量选择的目的。两种回归都可以用来解决标准线性回归的过拟合问题。
一、岭回归（Ridge regression）
①岭系数
![X=[x_{ij}]_{m*(n+1)}](http://img.e-com-net.com/image/info8/e972ac735f2d4e25aa4e0460c1e6fb15.gif){kind=small}
，(第一列都是1)，m是样本数，n是维度，参数矩阵
，当
奇异或
很小时（复共线性或n+1>m）
的计算会出错，因此引入修正因子岭系数
使得
是满秩矩阵，
是(n+1)阶单位矩阵，被修正为
②代价函数（Costfunction）
其中
是
正则化项（2范数的平方），也叫正则化系数或惩罚系数，值越大，正则化越强。对于“惩罚”的理解：引入参数矩阵是为了提炼模型，是一个简化的步骤，降低了复杂度，引入“惩罚”进行修正。当
时即为最小二乘法（Least square method）；当
时
③参数矩阵的解
④岭系数的确定
Ⅰ、岭迹法
岭估计的回归系数中岭参数的选择是一个十分重要的问题，使用较多的方法是岭迹法。岭迹法中选择k值的一般原则是：(1)各回归系数的岭估计基本稳定；(2) 用最小二乘法估计时符号不合理的回归系数，其岭估计的符号将变得合理；(3)回归系数没有不合乎经济意义的绝对值；(4)残差平方和增加不太多。岭迹法确定k值缺少严格的令人信服的理论依据，存在着一定的主观人为性，这似乎是岭迹法的一个明显的缺点。但是，岭迹法确定k值的这种人为性正好是发挥定性分析与定量分析有机结合的地方。
是关于（岭系数）的函数，绘制曲线即为岭迹图。
如何阅读岭迹图？
1. 了解横轴和纵轴的含义。通常，岭迹图的横轴表示正则化参数，纵轴表示特征系数的值。正则化参数是用于控制模型复杂度的参数，它越大，模型的复杂度就越低。特征系数表示不同特征在模型中的重要性。
2. 查看岭迹图的形状。岭迹图通常呈现出一个平滑的曲线，这条曲线反映了正则化参数对特征系数的影响。如果曲线呈现出急剧的变化，说明正则化参数对模型产生了较大的影响。
3. 分析曲线的峰值。曲线的峰值表示正则化参数的最佳取值，使得模型的效果最佳。在峰值处，不同特征的系数都有一个最优的取值，表示这些特征在模型中的贡献最大。
4. 比较不同曲线的差异。如果有多条曲线，可以比较它们的峰值和形状，以了解不同正则化参数对模型的影响。如果不同曲线的峰值相似，那么这些曲线可能对应着类似的模型，可以进行进一步的比较和分析。
load('data.mat')
x0=data(:,[3,4,5]);
y=data(:,2);
m=size(x0,1);
x=[ones(m,1),x0];
[m,n]=size(x);
e=eye(n);
for k=0:1:10000
theta(:,k+1)=(x'*x+k/10*e)^(-1)*x'*y;
end
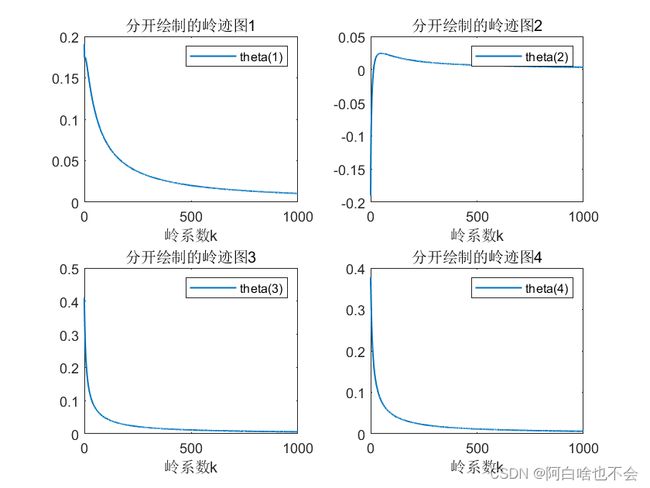
%分开绘制
for i=1:n
subplot(2,2,i)
plot((0:1:10000)/10,theta(i,:),'LineWidth',1)
title({['分开绘制的岭迹图',num2str(i)]})
legend({['theta(',num2str(i),')']})
hold on
end
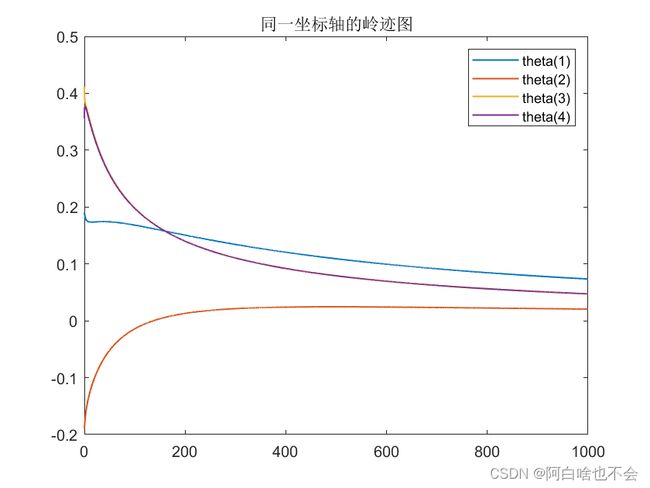
%一起绘制
figure
for i=1:n
plot((0:1:10000)/10,theta(i,:),'LineWidth',1)
legends([i])={['theta(',num2str(i),')']};
hold on
end
legend(legends);
title('同一坐标轴的岭迹图')
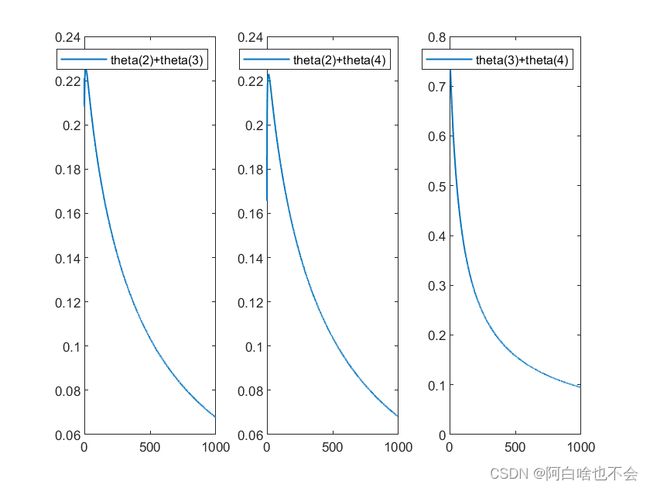
%参数两两和和的绘制
figure
for i=2:(n-1)
for j=(i+1):n
subplot(1,3,i+j-4)
plot((0:1:10000)/10,theta(i,:)+theta(j,:),'LineWidth',1)
legend({['theta(',num2str(i),')','+theta(',num2str(j),')']})
hold on
end
endMATLAB中的ridge函数可用来做岭回归分析的，参数说明如下
b=ridge(y,x,k,s);
%b是岭回归模型中的系数向量β=[β0，β1，β2，...，βn],β0是常数项，β1到βn是自变量x1到xn对应的系数
%y是因变量向量
%x是自变量矩阵，x=[x1,...,xn],每个xi都是列向量
%k是岭参数，岭参数不同，岭回归模型不同，要选取合适的岭参数
%s这个位置的参数只能填0或1，或者不填默认为0。0表示输出的系数β该是多少就是多少，1表示输出系数β是标准化后的
Ⅱ、迭代法
根据Hoerl、Kernard和Baldwin(1975)提出的方法取k的固定值。具体确定方法如下：对于标准化的回归模型
,
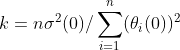，其中
是修正后的样本维度，
是回归方程的残差均方，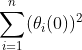
是最小二乘的参数矩阵2范数的平方。
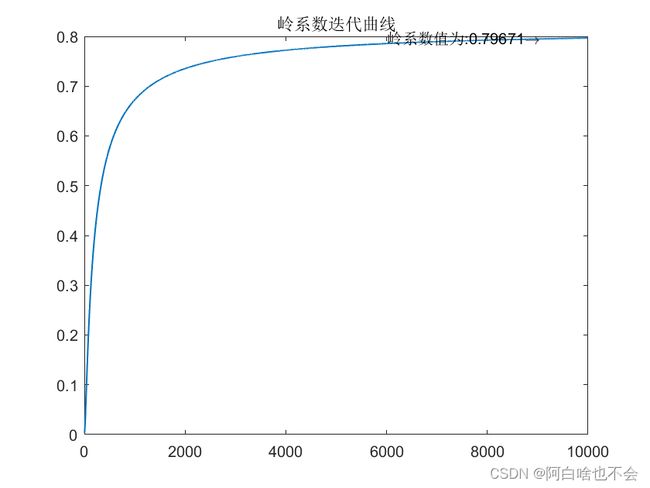
%迭代法确定k
k0=n*var(y-x*theta(:,1))/(theta(:,1)'*theta(:,1));
ik(1)=k0;
for j=2:10000
k1=n*var(y-x*theta(:,j))/(theta(:,1)'*theta(:,1));
ik(j)=k1;
if (abs(k0-k1)>1e-07)
k0=k1;
else
break
end
end
plot(ik,'LineWidth',1)
text(size(ik,2)-4000,ik(end),{['岭系数值为:',num2str(ik(end)),'\rightarrow']})
title('岭系数迭代曲线')
%最后得到的参数矩阵
theta_last=(x'*x+k0*e)^(-1)*x'*y
figure
y1=x*theta(:,1);
y2=x*theta_last;
error1=y-x*theta(:,1);
error2=y-x*theta_last;
plot(1:m,error1,1:m,error2,[1,m],[0,0],'LineWidth',1)
legend([{'最小二乘法'},{['岭系数=',num2str(k0)]}])
title('残差曲线');
theta_last =
0.1900
-0.1887
0.4037
0.3630二、LASSO回归（Least Absolute Selection and Shrinkage Operator）
LASSO 回归的特点是在拟合广义线性模型的同时进行变量筛选（variable selection）和复杂度调整（regularization）。因此不论目标因变量（dependent/response varaible）是连续的（continuous），还是二元或者多元离散的（discrete），都可以用 LASSO 回归建模然后预测。
这里的变量筛选是指不把所有的变量都放入模型中进行拟合，而是有选择的把变量放入模型从而得到更好的性能参数。复杂度调整是指通过一系列参数控制模型的复杂度，从而避免过度拟合（overfitting）。Lasso回归也存在一些缺点，Lasso回归无法得出显式解，智能使用近似化的计算法（坐标轴下降法和最小角回归法）估计出来的结果不太稳定，存在一定的误差。
LASSO回归与岭回归的不同在于代价函数的差异。
①代价函数
，
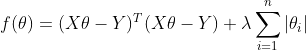是
正则化项。与岭回归的不同在于，此约束条件使用了绝对值的一阶惩罚函数代替了平方和的二阶函数。
②惩罚系数的确定
Lasso回归的惩罚系数可以通过交叉验证来确定，具体步骤如下：
1. 将数据集分成训练集和验证集
2. 对于每个可能的惩罚系数值（例如，通过对数空间进行网格搜索），在训练集上拟合Lasso模型
3. 使用训练集上拟合的模型对验证集进行预测，并计算预测误差
4. 重复步骤2-3，直到测试完所有可能的惩罚系数值
5. 选择具有最小平均预测误差的惩罚系数
6. 使用最终选择的惩罚系数在整个数据集上训练Lasso模型
这种方法称为交叉验证。它可以减少过度拟合和选择较好的惩罚系数。
%将(MISSING)数据分为训练集和测试集
load('data.mat')
x0=data(:,[3,4,5]);
y=data(:,2);
m=size(x0,1);
x=[ones(m,1),x0];
[m,n]=size(x);
cv = cvpartition(size(x,1),'Holdout',0.3);
%cvpartition函数是Matlab中用于交叉验证的函数。它可以将数据集分成训练集和测试集，
% 以便评估模型的性能。cvpartition函数可以根据不同的交叉验证方法，如K折交叉验证、
% 留一交叉验证等，将数据集分成不同的训练集和测试集。同时，cvpartition函数还可以
% 根据指定的比例将数据集分成训练集和测试集。
Xtrain = x(cv.training,:);
ytrain = y(cv.training,:);
Xtest = x(cv.test,:);
ytest = y(cv.test,:);
%!使(MISSING)用交叉验证确定最优的lambda值
[B,FitInfo] = lasso(Xtrain,ytrain,'CV',10);
lassoPlot(B,FitInfo,'PlotType','Lambda','XScale','log');
bestLambda = FitInfo.LambdaMinMSE;
③参数矩阵的解
由于引入的惩罚项是绝对值的一阶函数，不可导，因此无法使用偏导进行计算。主要有两种求解参数矩阵的方法——坐标下降法（Coordinate descent）和最小角回归法（Least Angle Regression，LARS）
Ⅰ、坐标下降法（Coordinate descent）
从岭迹法可以看出它更多是用来判断某个维度数据对模型的影响和维度间的线性相关问题，在确定岭系数时存在精度问题。坐标下降法（Coordinate descent）通过迭代可以解决精度问题。
坐标下降法步骤：
1、初始化参数矩阵theta，一般都取0
2、遍历所有权重系数，依次将其中一个权重系数作为变量
3、当权重系数变化不大或达到最大迭代次数时结束迭代
从坐标下降法的思路可以发现粒子群法(Particle Swarm Optimization，PSO)可以用来解决参数矩阵的确定，关于PSO可以参考阿白数模笔记之粒子群法(Particle Swarm Optimization，PSO)负反馈（Degenerative Feedback）修正及MATLAB代码详解
代价函数：
function v=cost(x,y,t,k)
%x是m*(n+1)矩阵，y是函数值,t是1*（n+1）参数矩阵,k是岭系数
v=(y-x*t)'*(y-x-t)+k*sum(abs(t));
endPSO求解
%坐标下降法，粒子群法
N = 100; %群体粒子个数
D = n; %粒子维数
T = 200; %最大迭代次数
c1 = 1.5; %正反馈调节因子1
c2 = 1.5; %正反馈调节因子2
c3=-0.3;%负反馈调节因子1
c4=-0.3;%负反馈调节因子2
Wmax = 0.9; %惯性权重最大值
Wmin = 0.4; %惯性权重最小值
Xmax = 10; %位置最大值
Xmin = 0; %位置最小值
Vmax = 1; %速度最大值，当更新后速度v>Vmax，取v=Vmax
Vmin = -1; %速度最小值,当更新后速度vgworst)
gw=p(i,:);
gworst=pbest(i);
end
end
gb = ones(1,T);%记录每次迭代最优值
%%%%%%%%%按照公式依次迭代直到满足精度或者迭代次数%%%%%%%%
for i = 1:T
for j = 1:N
%%%%%%%%%更新个体最优位置和最优值%%%%%%%%%%%%%
if (cost(x,y,X(j,:),k)< pbest(j))
p(j,:) = X(j,:);
pbest(j) = cost(x,y,X(j,:),k);
%%%%%%%%%更新个体最差位置和最差值%%%%%%%%%%%%%
elseif (cost(x,y,X(j,:),k) >pworst(j))
pw(j,:)=X(j,:);
pworst(j)= cost(x,y,X(j,:),k);
end
%%%%%%%%%%更新全局最优位置和最优值%%%%%%%%%%%%
if(pbest(j) < gbest)
g = p(j,:);
gbest = pbest(j);
%%%%%%%%%%更新最差位置和最差值%%%%%%%%%%%%
elseif (pworst(j) > gworst)
gw=p(j,:);
gworst=pworst(j);
end
%%%%%%%%%%%计算动态惯性权重值%%%%%%%%%%%%%%%
w = Wmax-(Wmax-Wmin)*i/T;%线性递减公式
%%%%%%%%%%%%更新位置和速度值%%%%%%%%%%%%%%%
v(j,:) = w*v(j,:)+c1*rand*(p(j,:)-X(j,:))...
+c2*rand*(g-X(j,:))+c3*rand*(pw(j,:)-X(j,:))+c4*rand*(gw-X(j,:));
X(j,:) = X(j,:)+v(j,:);
%%%%%%%%%%%%%%边界条件处理%%%%%%%%%%%%%%%
for ii = 1:D
if (v(j,ii) > Vmax) | (v(j,ii) < Vmin)
v(j,ii) = rand * (Vmax-Vmin)+Vmin;
end
if (X(j,ii) > Xmax) | (X(j,ii) < Xmin)
X(j,ii) = rand * (Xmax-Xmin)+Xmin;
end
end
end
%%%%%%%%%%%%%%记录历代全局最优值%%%%%%%%%%%%%%
gb(i) = gbest;
end
g %最优个体
gb(end) %最优值
figure
plot(gb)
xlabel('Iterations');
ylabel('Fitness value');
title('Fitness evolution curve')
g =
0.0794 0.0567 0.0603 0.8174
ans =
0.1344 结果分析，MATLAB中lasso函数也可进行参数矩阵求解
%!使(MISSING)用最优的lambda值进行lasso回归
[B,FitInfo] = lasso(Xtrain,ytrain,'Lambda',bestLambda);
yhat = Xtest*B + FitInfo.Intercept;
%!计(MISSING)算测试集的均方误差
mse = mean((yhat - ytest).^2);
disp(['Test MSE: ' num2str(mse)]);
intercept=FitInfo.Intercept;%截距
y3=x*B+intercept;
error3=y-y3;y4=x*g';
error4=y-x*g';
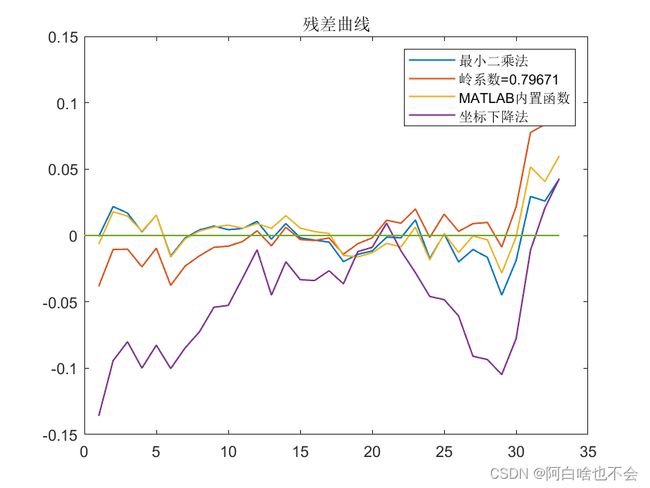
plot(1:m,error1,1:m,error2,1:m,error3,1:m,error4,[0,m],[0,0],'LineWidth',1)
legend([{'最小二乘法'},{['岭系数=',num2str(k0)]},{'MATLAB内置函数'},'坐标下降法'])
title('残差曲线');
figure
plot(1:m,y,1:m,y1,1:m,y2,1:m,y3,1:m,y4,'LineWidth',1)
legend([{'原始数据'},{'最小二乘法'},{['岭系数=',num2str(k0)]},{'MATLAB内置函数'},'坐标下降法'])
Ⅱ、最小角回归法（Least Angle Regression，LARS）
LARS是Efron于2004年提出的一种变量选择的方法，类似于向前逐步回归(Forward Stepwise)的形式。从解的过程上来看它是lasso regression的一种高效解法。MATLAB内置函数lasso采用的便是最小角回归。故下图的最小角回归与内置函数的图样重合。
[B,FitInfo] = lasso(trainX,trainY,'Alpha',1,'CV',10);
B存储了Lasso算法得出的系数向量，即训练集中每个特征的重要性权重。这些系数可以用于预测新的观测值或者做特征选择。FitInfo是一个结构体，它包含了关于Lasso模型的一些统计信息，例如每次交叉验证的误差、正则化参数的路径等。
% 加载数据
load('data1.mat')
% 将数据分为训练集和测试集
trainData = data1(1:30,:);
testData = data1(31:end,:);
% 将训练集和测试集分为特征和标签
trainX = trainData(:,1:end-1);
trainY = trainData(:,end);
testX = testData(:,1:end-1);
testY = testData(:,end);
% 进行最小角回归
[B,FitInfo] = lasso(trainX,trainY,'Alpha',1,'CV',10);
% 打印最小角回归的结果
fprintf('最小角回归的结果：\n');[B,FitInfo] = lasso(trainX,trainY,'Alpha',1,'CV',10);
fprintf('选择的特征数量：%d\n',sum(B(:,FitInfo.IndexMinMSE)~=0));
fprintf('最小均方误差：%f\n',FitInfo.MSE(FitInfo.IndexMinMSE));
% 使用最小角回归的结果进行预测
predY = testX*B(:,FitInfo.IndexMinMSE) + FitInfo.Intercept(FitInfo.IndexMinMSE);
% 计算预测结果的均方误差
mse = mean((predY-testY).^2);
% 打印预测结果的均方误差
fprintf('预测结果的均方误差：%f\n',mse);
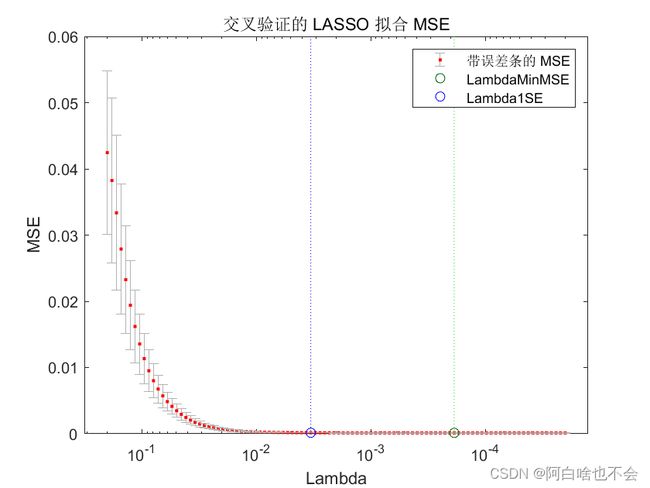
lassoPlot(B,FitInfo,'PlotType','CV');
legend('show') % Show legend
%!找(MISSING)到交叉验证误差最小的索引
minMSEIdx = find(FitInfo.MSE == min(FitInfo.MSE));
%!最(MISSING)后的权重系数矩阵
finalB = B(:,minMSEIdx);
intercept=FitInfo.Intercept;%截距
y5=x*finalB+intercept(minMSEIdx);
error5=y-y5;
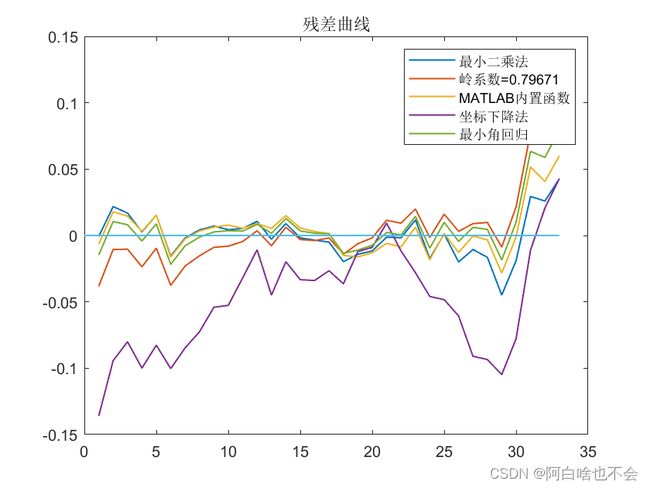
plot(1:m,error1,1:m,error2,1:m,error3,1:m,error4,1:m,error5,[0,m],[0,0],'LineWidth',1)
legend([{'最小二乘法'},{['岭系数=',num2str(k0)]},{'MATLAB内置函数'},'坐标下降法','最小角回归'])
title('残差曲线');
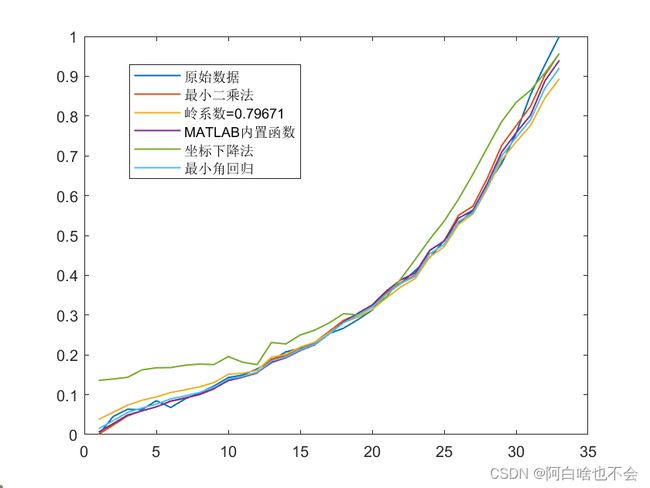
figure
plot(1:m,y,1:m,y1,1:m,y2,1:m,y3,1:m,y4,1:m,y5,'LineWidth',1)
legend([{'原始数据'},{'最小二乘法'},{['岭系数=',num2str(k0)]},{'MATLAB内置函数'},'坐标下降法','最小角回归'])