针对语义分割的真实世界的对抗样本攻击
针对语义分割的真实世界的对抗样本攻击
来自于论文"Evaluating the Robustness of Semantic Segmentation for Autonomous Driving against Real-World Adversarial Patch Attacks"
代码在[github](https://github. com/retis-ai/SemSegAdvPatch)有开源,各位感兴趣的可以自己去跑跑看。
文章的主要贡献:
- 提出了一种像素级别的交叉熵误差,用于生成强大的对抗补丁(adversarial patch)
- 使用3D世界的几何信息来构造对抗补丁
- 充分的实验,在Cityscape,CRALA和真实世界上进行测试
攻击概述
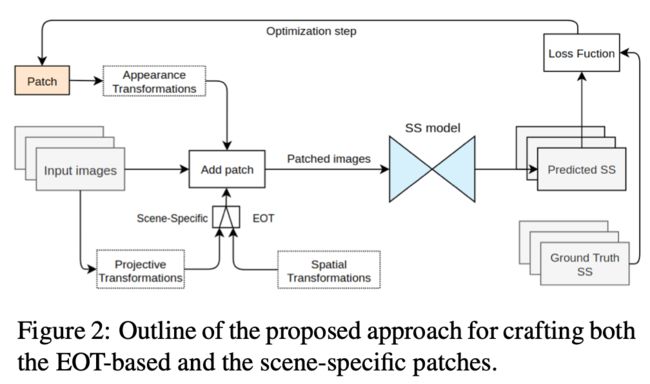
如上图所示的流程:
- 首先输入图片
- 图片会经过投影变换和空域变换,
- 然后传入到一个场景特定的EOT生成对应的补丁, EOT是指 Expectation Of Transformation
- EOT一般用来生成真实世界可用的对抗样本,使得对抗样本对真实世界的一些变换鲁棒
- 将打补丁之后的图片输入到SS模型之中,SS指Semantic Segmentation,也就是语义分割
- 得到语义分割的结果并优化对应的补丁
基于EOT的攻击
这里首先给出EOT攻击的形式化描述:
δ ∗ = arg max δ E x ∈ X , ζ a ∈ Γ a , η ∈ Γ L ( f ( x ~ ) , y ) \delta^* = \arg\max_{\delta}\mathbb{E}_{x\in\mathcal X, \zeta_a\in \Gamma_a,\eta\in \Gamma} \mathcal L(f(\tilde{x}), y) δ∗=argδmaxEx∈X,ζa∈Γa,η∈ΓL(f(x~),y)
其中 δ ∗ \delta^* δ∗ 代表最优的补丁, Γ \Gamma Γ 是空域变换的空间(包括平移、缩放等), Γ a \Gamma_a Γa 代表对实体的变换(包括明亮度、对比度、噪声等)
其中 x ~ = x + δ ∗ \tilde{x} = x + \delta^* x~=x+δ∗ 代表加上了最优补丁的输入
总的来说,EOT和普通对抗样本的区别其实在于,多了一些可能的变换,是的对抗样本具备更强的鲁棒性。
误差函数设计
有了EOT攻击的概述,我们只需要定义好误差函数,就可以对补丁进行梯度下降,进而搜索到好的对抗补丁了
这篇文章采用的是,较为简单的交叉熵误差,定义如下:
L C E ( p i , y i ) = − ∑ i y i log p i \mathcal L_{CE}(p_i, y_i) = -\sum_i y_i\log p_i LCE(pi,yi)=−i∑yilogpi
其中 y i ∈ { 0 , 1 } y_i\in\{0,1\} yi∈{0,1} 代表是否是正确类别, p i p_i pi 是指模型在 i i i 类别上的输出
对于语义分割而言,我可以把输出的每一个像素点位置当成是分类任务。
我们可以定义一个集合 P P P, 该集合包括除了补丁位置之外所有的像素位置,且这些像素位置被正确分类
P = { i ∈ N / N ~ ∣ S S i ( x ~ ) = y i } P = \{i\in \mathcal N /\ \tilde{\mathcal N} | SS_i(\tilde{x})=y_i\} P={i∈N/ N~∣SSi(x~)=yi}
其中 N \mathcal N N 代表所有像素的位置, N ~ \tilde{\mathcal N} N~ 代表补丁覆盖的像素位置, x ~ \tilde{x} x~ 代表加了补丁的图像, S S i ( x ~ ) SS_i(\tilde{x}) SSi(x~) 代表对应输出的第 i i i 个像素的位置的输出。
那么逐个像素的交叉熵误差可以被分成两个部分:
L 1 = ∑ i ∈ P L C E ( f i ( x ~ ) , y i ) L 2 = ∑ i ∉ P L C E ( f i ( x ~ ) , y i ) \mathcal L_1 =\sum_{i\in P} \mathcal L_{CE}(f_i(\tilde{x}), y_i)\\ \mathcal L_2 = \sum_{i\notin P} \mathcal L_{CE}(f_i(\tilde{x}), y_i) L1=i∈P∑LCE(fi(x~),yi)L2=i∈/P∑LCE(fi(x~),yi)
这两个部分分别代表,补丁区域的输出误差以及补丁区域之外的输出误差
我们可以定义出一个融合误差,表示成他们的线性组合,进而计算出梯度:
∇ δ L ( f ( x ~ ) , y ) = γ ⋅ ∇ δ L 1 ∣ ∣ ∇ δ L 1 ∣ ∣ + ( 1 − γ ) ⋅ ∇ δ L 2 ∣ ∣ ∇ δ L 2 ∣ ∣ \nabla_\delta \mathcal L(f(\tilde{x}), y) = \gamma \cdot \frac{\nabla_{\delta}\mathcal L_1}{||\nabla_{\delta}\mathcal L_1||}+ (1-\gamma)\cdot\frac{\nabla_{\delta}\mathcal L_2}{||\nabla_{\delta}\mathcal L_2||} ∇δL(f(x~),y)=γ⋅∣∣∇δL1∣∣∇δL1+(1−γ)⋅∣∣∇δL2∣∣∇δL2
实验结果
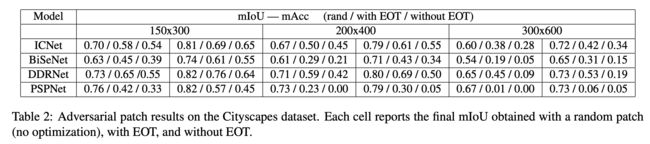
这里我们简单看一下在Cityscapes数据集上的实验结果,如上表所示。
Cityscapes是一个驾驶图像的数据集,其图片分辨率为1024x2048,其中2975张用于训练,500张用于测试。
表中的150x300,200x400,300x600是指补丁的大小。
rand/with EOT/without EOT 分别代表随机噪声,用EOT的对抗补丁,不用EOT的对抗补丁。
有几个容易得到的结论:
- 随着补丁范围的增加,正确率下降越明显
- EOT的效果要优于不加EOT的效果
- DDRNet的鲁棒性看上去是最佳的