狗都能看懂的VAE笔记

生成模型Auto-Encoder一直是一个非常有创造性的方向。期中的VAE变分编码器一直是我没搞懂的部分，在AI绘画突然火起来的时候，不得不搞清楚VAE了。看了很多VAE的讲解，没有良好的数学基础，看的我是云里雾里，终于看了众多大神的讲解，搞清楚了VAE设计的思路和解决的问题。所以此博客不涉及数学的推导，只从直观的理解和作用上讲解。

自编码器

自编码器是生成模型的一种，输入为一张图，通过Encoder压缩成低维特征之后，再利用Decoder恢复成原图。它的优化目标是输入$X$与输出$\hat{X}$越接近越好，所以可以选择L2Loss作为重构Loss。这里插一句题外话，可能大家会认为Auto-Encoder会在压缩图像领域很流行，但实际上是在去噪领域比较常用。输入带噪声的图像，输出不带噪声的原图图像。

普通Auto-Encoder的问题

除了Encoder的部分，自编码器还有的Decoder部分。那这里我们可以想象下，如果取出一个训练好的自编码器Decoder部分，给他输入一组vector，是不是可以创造出新的图像？理想确实是这样，但现实是，随便输入一组数据，它大概率生成的是一张毫无逻辑的噪声图。

那为什么会这样呢？

• 直观上理解：你训练出来的这个AE只是尽可能的在还原输入图像，你无法限制它内部的Encoder部分是真的在学如何压缩有用的特征，而Decoder也一样，无论怎么样都会把Encoder压缩的特征还原回去。所以Encoder和Decoder实际上达成了一种“默契”，它们自己有加密通话，只对训练数据有效，换组数据就解密不了了。因此，它不关心编码数据是否真的有特征，它只需要完美的还原回去就行了。所以普通的AE就相当于是模型在自嗨。

• 从数学角度理解：在不加限制的情况下，我们把数据压缩到极致的时候，输入高维的特征实际上已经是在“一条线”上，编码结果已经丧失了可分性。我们希望它是被压缩成右边这个样子，在编码后仍具有可分性。

解决的方法

我们刚刚说了不加限制的情况，产生的编码是毫无意义的。由于自动编码器模型可以自由地编码潜在向量，我们可以想象，潜在空间可能会有很多区域，其中的空白区域会产生随机/不可解释的输出，如图中的空白区域所示。我们希望具有有意义输出的潜在空间区域是连续的，而不是像下图那样是分开的，这样可以方便地在不同属性之间进行插值。

有了“限制条件”，我们可以防止模型对潜在空间中相距很远的数据进行编码，并鼓励尽可能多的返回分布“重叠”，当Encoder编码出来的分布如下图所示，从而满足预期的连续性和完整性条件，我们才可以获得有效数据。

举个例子

想象一下上面的例子，自动编码器将图像编码为表示照片中的微笑的潜在属性(在真实的训练中，我们不知道每个属性实际表示什么，这样举例更好理解)。普通的自动编码器将为潜属性提供一个值，但变分自动编码器将潜属性存储为属性的概率分布，如上面的图所示。

生成一个分布比生成一个具体的值更好，为什么这么说呢？对于一个连续的分布，在训练过程中你可以进行采样，这意味着，只要在这个分布上的任何采样点，你都可以生成一个同样大笑的脸。而在另一个分布上，你可以生成一个不笑的脸。虽然在两个分布重叠的地方，模型需要降分布学习成既像大笑，又像不笑的脸。这个过程，loss值可能会不太好看，导致训练不稳定。但这样模型就可以获得一张微笑的脸，这个过程我们可以看成是一种正则化，不让AE过拟合。

这就是VAE和普通AE的区别了。

如何运作

当我理解了VAE设计初衷之后（将编码结果存储为概率分布时），第二个问题是如何得到一个分布？

我们做了一个重要的假设来简化这个过程。我们假设潜在分布总是高斯分布。高斯分布可以很容易地用两个值来描述，即均值和方差或标准差(可以从方差计算出标准差)。你也可以把它用其他任何分布表示，只是生活中大部分问题都可以高斯分布解释。

所以VAE的模型就变成了下面这个样子，Encoder输入图像，输出均值的和方差。

但是，此抽样过程需要额外的关注。训练模型时，我们需要能够使用称为反向传播的技术来计算网络中每个参数在最终输出损失方面的关系。但是，我们根本无法为随机抽样过程做到这一点。不过，我们可以利用一个被称为“重参数化“的聪明想法，我们从单位正态分布中$\epsilon$随机采样，乘上方差$\sigma$，加上均值$\mu$。

通过重新参数化，我们现在可以优化分布的参数，同时仍然保持从该分布中随机抽样的能力。下面是反向传播的计算过程。

论文和源码在计算时，会对$\sigma$取log，那是因为方差计算出来都是正值，取log之后可以让它变为负的，使得其探索更多的潜在分布。

数学细节

这里会有点难懂，但我会尽可能清晰的讲解。不感兴趣的同学可以跳过。

现在假设存在一个分布z可以生成x。Decoder自然地由$p(x|z)$定义**，它描述了给定编码变量的解码变量的分布**，而Encoder由$p(z|x)$定义**，它描述了给定解码变量的编码变量**。我们只能看的到x，但我们想计算z的特征，换句话说，计算$p(z|x)$，那么利用贝叶斯公式可得：
$$p(z|x)=\frac{p(x|z)p(z)}{p(x)}$$
其中
$$p(x)=\int p(x|z)p(z)dz$$
计算$p(x)$相当困难，这通常是一个棘手的分布。然而，我们可以应用变分推理来估计这个值。

让我们通过另一个分布$q(z|x)$来近似$p(z|x)$，如果我们可以通过定义$q(z|x)$的参数，使它非常类似于$p(z|x)$，我们可以用它来执行难处理分布的近似推理。

其实简单来说就是，$p(z|x)$长什么样我不知道，我可以用一个已知的$q(z|x)$去近似它。而一般用来衡量两个分布是否一致的损失函数是KL散度。所以当我们优化的时候，只需要最小化KL散度即可：
$$minKL(q(z|x)||p(z|x))$$
Ali Ghodsi 博士在这里进行了完整的推导，所以最终的损失就是：
$$L(x,\hat{x})+\sum _{j}KL(q_j(z|x)||p(z))$$
第一项是重构损失，即重构输出与输入之间的差值，通常使用均方误差(MSE)。第二项是真实分布$p(z)$与我们选择的分布$q(z|x)$之间的KL散度，其中q通常是一个均值和单位方差为零的正态分布N(0,1)。鼓励分布$q(z|x)$在训练中接近真实分布$p(z)$。

最后让我们来更直观的比较，这两项的作用

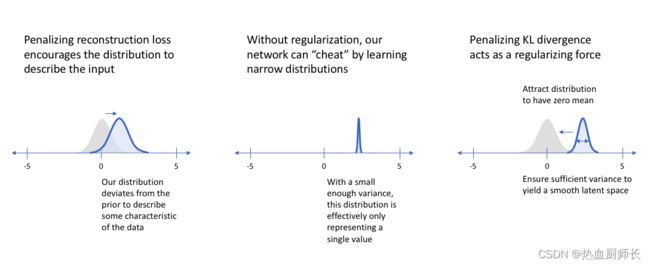
只使用重构损失时就是普通的AE，又会遇到之前说的问题。但是，如果我们只专注于用我们的KL散度损失项模拟先验分布，我们将会将每个单位z描述为单位正态分布，而不能描述原始数据。所以需要结合两者一起优化。