【数据分析与挖掘】数据预处理
目录
- 概述
- 一、数据清洗
-
- 1.1 缺失值处理
-
- 1.1.1 拉格朗日插值法
- 1.1.2 牛顿插值法
- 1.2 异常值处理
- 二、数据集成
-
- 2.1 实体识别
- 2.2 冗余属性识别
- 三、数据变换
-
- 3.1 简单函数变换
- 3.2 规范化
- 3.3 连续属性离散化
- 3.4 属性构造
- 3.5 小波变换
- 四、数据规约
-
- 4.1 属性规约
- 4.2 数值规约
概述
数据挖掘过程中,数据预处理占整个过程的60%,主要分为以下四个步骤:

一、数据清洗
数据清洗的主要目的是为了删除原始数据集中的无关数据、重复数据、平滑噪声数据、处理缺失值、异常值等。
1.1 缺失值处理
处理缺失值的方法可分为三类:删除数据、数据插补和不处理,常见的数据插补方法见下表:

插值法有:Hermite插值、分段插值、样条插值法,而最主要的有拉格朗日插值法和牛顿插值法。
1.1.1 拉格朗日插值法
def lagrange_interpolation(x, y, x_int):
"""
使用拉格朗日插值法计算函数在指定点的值
:param x: 函数自变量的取值列表
:param y: 函数因变量的取值列表
:param x_int: 指定点的自变量取值
:return: 指定点的函数值
"""
n = len(x)
assert n == len(y), "输入的 x 和 y 列表长度不一致"
# 定义拉格朗日插值函数
def L(k):
lk = 1
for i in range(n):
if i != k:
lk *= (x_int - x[i]) / (x[k] - x[i])
return lk
# 计算插值函数的值
f_int = 0
for k in range(n):
f_int += y[k] * L(k)
return f_int
import math
# 定义自变量和因变量列表
x = [0, 0.25, 0.5, 0.75, 1]
y = [math.sin(xx) for xx in x]
# 计算插值函数在 x=0.5 处的值
x_int = 0.5
f_int = lagrange_interpolation(x, y, x_int)
# 输出结果
print("f({:.2f}) = {:.4f}".format(x_int, f_int))
1.1.2 牛顿插值法
def newton_interpolation(x, y, x_int):
"""
使用牛顿插值法计算函数在指定点的值
:param x: 函数自变量的取值列表
:param y: 函数因变量的取值列表
:param x_int: 指定点的自变量取值
:return: 指定点的函数值
"""
n = len(x)
assert n == len(y), "输入的 x 和 y 列表长度不一致"
# 计算差商
f = [[y[i]] for i in range(n)]
for j in range(1, n):
for i in range(j, n):
f[i].append((f[i][j - 1] - f[i - 1][j - 1]) / (x[i] - x[i - j]))
# 计算插值函数的值
f_int = f[0][0]
for i in range(1, n):
term = f[i][i]
for j in range(i):
term *= (x_int - x[j])
f_int += term
return f_int
import math
# 定义自变量和因变量列表
x = [0, 0.25, 0.5, 0.75, 1]
y = [math.sin(xx) for xx in x]
# 计算插值函数在 x=0.5 处的值
x_int = 0.5
f_int = newton_interpolation(x, y, x_int)
# 输出结果
print("f({:.2f}) = {:.4f}".format(x_int, f_int))
1.2 异常值处理
在数据预处理时,异常值是否提出,需要根据具体情况,有些异常值可能蕴含某些信息。

二、数据集成
数据挖掘需要的数据往往分布在不同的数据源中,数据集成就是将多个数据源合并存放在一个一致的数据存储中的过程。
在数据集成时,来自于多个数据源的现实世界实体的表达形式是不一样的,不一定是匹配的,要考虑实体识别问题和属性冗余问题,从而把数据源在最底层上加以转化、提炼和集成。
2.1 实体识别
实体识别的任务是检测和解决同名异义、同名同义、单位不统一的冲突。如:
- 同名异义:数据源A中的属性ID和数据源B中的属性ID分别描述的是菜品编号和订单编号,描述的是不同实体。
- 同名同义:数据源A中的sales_dt和数据源B中的sales_dt都是描述销售日期的,即:A.sales_dt=B.sales_dt.
- 单位不统一:描述同一个实体分别用的是国际单位和中国传统的计量单位。
2.2 冗余属性识别
- 数据集成往往导致数据冗余,如:
- 同一属性多次出现
- 同一属性命名不一致导致重复
- 不同源数据的仔细整合能减少甚至避免数据冗余与不一致,以提高数据挖掘的速度和质量。对于冗余属性要先分析检测后再将其删除。
- 有些冗余属性可以用相关分析检测出。给定两个数值型属性A和B,根据其属性值,可以用相关系数度量一个属性在多大程度上蕴含另一个属性。
三、数据变换
主要是对数据进行规范化操作,将数据转换成“适当的”格式,以适用于挖掘任务及算法的需要。
3.1 简单函数变换
简单函数变换就是对原始数据进行某些数学函数变换,常用的函数变换包括平方、开方、对数、差分运算等,即:
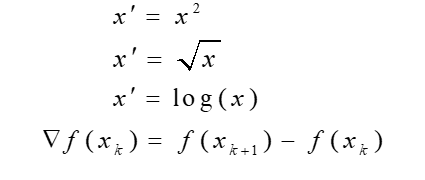
- 不正太分布的变成具有正太分布的数据
import numpy as np
from scipy.stats import boxcox
from sklearn.preprocessing import StandardScaler
# 定义非正态分布的数据
x = np.random.exponential(2, size=1000)
# 将数据进行 Box-Cox 变换
x_boxcox, _ = boxcox(x)
# 将变换后的数据进行标准化
scaler = StandardScaler()
x_norm = scaler.fit_transform(x_boxcox.reshape(-1, 1))
# 输出结果
print("原始数据的均值和标准差:{:.4f},{:.4f}".format(x.mean(), x.std()))
print("Box-Cox 变换后的数据的均值和标准差:{:.4f},{:.4f}".format(x_boxcox.mean(), x_boxcox.std()))
print("标准化后的数据的均值和标准差:{:.4f},{:.4f}".format(x_norm.mean(), x_norm.std()))
- 非平稳序列转化成平稳序列
import numpy as np
import pandas as pd
from statsmodels.tsa.stattools import adfuller
# 定义非平稳序列
x = np.cumsum(np.random.normal(0, 1, size=1000))
# 检验序列是否平稳
result = adfuller(x)
print("原始序列的 ADF 检验结果:p-value = {:.4f}".format(result[1]))
# 对序列进行一阶差分
x_diff = np.diff(x)
# 再次检验序列是否平稳
result = adfuller(x_diff)
print("差分后序列的 ADF 检验结果:p-value = {:.4f}".format(result[1]))
- 压缩变换等(PCA)
import numpy as np
from sklearn.decomposition import PCA
# 定义原始数据
x = np.random.normal(size=(100, 3))
# 使用 PCA 进行压缩变换
pca = PCA(n_components=2)
x_pca = pca.fit_transform(x)
# 输出结果
print("原始数据的形状:", x.shape)
print("PCA 变换后的数据的形状:", x_pca.shape)
3.2 规范化
数据标准化(归一化)处理是数据挖掘的一项基础工作,不同评价指标往往具有不同的量纲和量纲单位,数值间的差别可能很大,不进行处理可能会影响数据分析的结果,为了消除指标之间的量纲和大小不一致的影响,需要将数据进行标准化处理,将数据按照比例进行缩放,使之落入一个特定的区域,从而进行综合分析。
有三种常用的规范化方法:最大最小值规范化、零均值规范化、小数定标规范化。
# -*- coding: utf-8 -*-
# 代码4-2 数据规范化
import pandas as pd
import numpy as np
datafile = '../data/normalization_data.xls' # 参数初始化
data = pd.read_excel(datafile, header = None) # 读取数据
print(data)
(data - data.min()) / (data.max() - data.min()) # 最小-最大规范化
(data - data.mean()) / data.std() # 零-均值规范化
data / 10 ** np.ceil(np.log10(data.abs().max())) # 小数定标规范化
3.3 连续属性离散化
一些数据挖掘算法,特别是某些分类算法,要求数据是分类属性形式,如ID3算法、Apriior算法等。这样,需要将连续属性变化成类别属性,即连续属性离散化。
常用的离散化方法:
等宽法、等频法、基于聚类分析的方法。
# -*- coding: utf-8 -*-
# 代码4-3 数据离散化
import pandas as pd
import numpy as np
datafile = '../data/discretization_data.xls' # 参数初始化
data = pd.read_excel(datafile) # 读取数据
data = data[u'肝气郁结证型系数'].copy()
k = 4
d1 = pd.cut(data, k, labels = range(k)) # 等宽离散化,各个类比依次命名为0,1,2,3
#等频率离散化
w = [1.0*i/k for i in range(k+1)]
w = data.describe(percentiles = w)[4:4+k+1] # 使用describe函数自动计算分位数
w[0] = w[0]*(1-1e-10)
d2 = pd.cut(data, w, labels = range(k))
from sklearn.cluster import KMeans # 引入KMeans
kmodel = KMeans(n_clusters = k, n_jobs = 4) # 建立模型,n_jobs是并行数,一般等于CPU数较好
kmodel.fit(np.array(data).reshape((len(data), 1))) # 训练模型
c = pd.DataFrame(kmodel.cluster_centers_).sort_values(0) # 输出聚类中心,并且排序(默认是随机序的)
w = c.rolling(2).mean() # 相邻两项求中点,作为边界点
w = w.dropna()
w = [0] + list(w[0]) + [data.max()] # 把首末边界点加上
d3 = pd.cut(data, w, labels = range(k))
def cluster_plot(d, k): # 自定义作图函数来显示聚类结果
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.figure(figsize = (8, 3))
for j in range(0, k):
plt.plot(data[d==j], [j for i in d[d==j]], 'o')
plt.ylim(-0.5, k-0.5)
return plt
cluster_plot(d1, k).show()
cluster_plot(d2, k).show()
cluster_plot(d3, k).show()
3.4 属性构造
在数据挖掘的过程中,为了帮助提取有用的信息、挖掘更深层次的模式,提高挖掘结果的精度,需要利用已有的属性集构造出新的属性,加入到现有集合中。
3.5 小波变换
# -*- coding: utf-8 -*-
# 代码4-5 小波变换特征提取代码
# 利用小波分析进行特征分析
# 参数初始化
inputfile= '../data/leleccum.mat' # 提取自Matlab的信号文件
from scipy.io import loadmat # mat是Python专用格式,需要用loadmat读取它
mat = loadmat(inputfile)
signal = mat['leleccum'][0]
import pywt # 导入PyWavelets
coeffs = pywt.wavedec(signal, 'bior3.7', level = 5)
# 返回结果为level+1个数字,第一个数组为逼近系数数组,后面的依次是细节系数数组
四、数据规约
数据规约是将海量数据进行规约,规约之后的数据扔接近于保持原数据的完整性,但数据量小很多。
通过数据规约,可以降低无效、错误数据对建模的影响,提高建模的准确性;少量且具有代表性的数据将大幅缩减数据挖掘所需的时间;降低存储数据的成本。
4.1 属性规约
属性规约常用的方法:合并属性、逐步向前选择、逐步向后删除、决策树归纳、主成分分析。
# -*- coding: utf-8 -*-
# 代码4-6 主成分分析降维
import pandas as pd
# 参数初始化
inputfile = '../data/principal_component.xls'
outputfile = '../tmp/dimention_reducted.xls' # 降维后的数据
data = pd.read_excel(inputfile, header = None) # 读入数据
from sklearn.decomposition import PCA
pca = PCA()
pca.fit(data)
pca.components_ # 返回模型的各个特征向量
pca.explained_variance_ratio_ # 返回各个成分各自的方差百分比
# 代码4-7 计算成分结果
pca = PCA(3)
pca.fit(data)
low_d = pca.transform(data) # 用它来降低维度
pd.DataFrame(low_d).to_excel(outputfile) # 保存结果
pca.inverse_transform(low_d) # 必要时可以用inverse_transform()函数来复原数据
low_d
4.2 数值规约
数值规约通过选择替代的、较小的数据来减少数据量。数据规约可以是有参的,也可以是无参的。有参方法是使用一个模型来评估数据,只需存放参数,而不需要存放实际数据,有参的数据规约技术主要有两种:回归(线性回归和多元回归)和对数线性模型(近似离散属性集中的多维概率分布)。数值规约常用方法有直方图、用聚类数据表示实际数据、抽样(采样)、参数回归法。








