图像处理-双边滤波和联合双边滤波

图像处理-双边滤波和联合双边滤波

双边滤波原理

​ 双边滤波(Bilateral Filter)是一种非线性滤波器，可以达到保持边缘，降噪平滑的效果。其算法最早由C. Tomasi和R. Manduchi在论文《Bilateral Filtering for Gray and Color Images》中提出，按照原文中的话说It combines gray levels or colors based on both their geometric closeness and their photometric similarity, and prefers near values to distant values in both domain and range. 双边滤波的权重不仅考虑了像素的欧氏距离（如普通的高斯低通滤波，只考虑了位置对中心像素的影响），还考虑了像素范围域中的辐射差异（例如卷积核中像素与中心像素之间相似程度、颜色强度，深度距离等），在计算中心像素的时候同时考虑这两个权重。

---

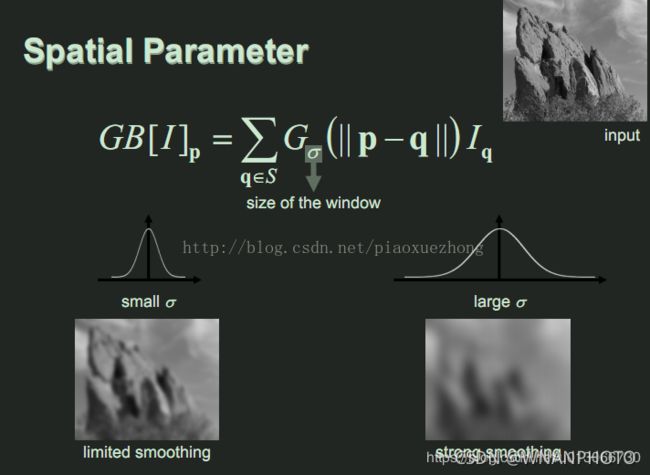
1. 空间权重：空间域（spatial domain S）与像素位置有关，为像素之间的距离(欧式距离)，定义为全局变量，通常定义如下：
   $$s(\xi ,x)=e^{-\frac{1}{2}(\frac{d(\xi ,x)}{\sigma {}_d}{)}^2}$$
   其中$d(\xi ,x)=||\xi -x||$表示两个像素之间的欧式距离，滤波过程如下：
   $$h(x)=k_d^{-1}(x){\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }f(\xi )s(\xi ,x)d\xi$$
   权值为：$k_d(x)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }s(\xi ,x)d\xi$

可以解释为：

2. 相似权重：像素范围域（range domain R）与像素值大小有关，为像素值之间的距离（辐射距离，相似性度量），根据像素值不同而不同，需要放在循环内，通常定义为：
   $$r(f(\xi ),f(x))=e^{-\frac{1}{2}(\frac{d(f(\xi ),f(x))}{\sigma {}_r}{)}^2}$$
   其中$d(f(\xi ),f(x))=||f(\xi )-f(x)||$表示两个像素之间的欧式距离，滤波过程如下：
   $$h(x)=k_r^{-1}(x){\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }f(\xi )r(f(\xi ),f(x))d\xi$$
   权值为：$k_r(x)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }r(f(\xi ),f(x))d\xi$

两者结合，得到基于空间距离，相似程度整体考虑的双边滤波如下：
$$h(x)=k^{-1}(x){\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }f(\xi )s(\xi ,x)r(f(\xi ),f(x))d\xi$$
权值为：$k(x)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }s(\xi ,x)r(f(\xi ),f(x))d\xi$

可以解释为：

双边滤波的两个权值的影响可以形象的解释为：

双边滤波的实现

实际应用时，根据需要对积分采用离散形式表示，滤波半径根据需要自行设置。

在进行滤波前，需将数据转换为浮点型等。

• matlab源码-gray图像

function fout = bilateralFilter_gray(fin,r,a,b)
%bilateralFilter_gray 灰度图像双边滤波
%   fout-滤波输出图像
%   fin-输入灰度图
%   r-滤波半径
%   a-全局标准差
%   b-局部标准差
%   双边滤波有两部分组成，一为空间权重:与像素位置有关(空域)，高斯滤波
%   另一为像素权重，与像素值(值域)大小有关，根据像素值大小不同而不同
%   空域滤波函数定义为c(x1) = e^(-(x1.^2)/(2*a^2)),均值为0，标准差为a的高斯分布
%   值域滤波函数定义为s(y1) = e^(-(y1.^2)/(2*b^2)),   
%   其中y1为滤波器大小范围内像素值与中心像素的距离，均值为0，标准差为b的高斯分布

c = fspecial('gaussian', 2*r+1, a);
fin  = im2double(fin);

h = waitbar(0,'Applying bilateral filter...');
set(h,'Name','Bilateral Filter Progress');

[m, n] = size(fin);
finTemp = padarray(fin, [r,r], 'symmetric');

fout = zeros(size(fin));


for i=r+1:m+r
    for j=r+1:n+r
        temp = finTemp(i-r:i+r,j-r:j+r);
        d = temp - finTemp(i, j);
        s = exp(-(d.^2)/(2*b^2));
        w = c.*s;
        fout(i-r, j-r) = sum(sum(temp.*w))/sum(w(:));
    end
    waitbar((i-r)/m);
end

• 实验结果

原图	滤波半径1，全局标准差3，局部标准差0.1
滤波半径3，全局标准差3，局部标准差0.1	滤波半径5，全局标准差3，局部标准差0.1
滤波半径5，全局标准差3，局部标准差0.5	滤波半径5，全局标准差3，局部标准差1

在实际应用中，一般选取较小的局部标准差和较大的滤波半径，取得的效果比较好。

• matlab源码-rgb图像

function fout = bilateralFilter_rgb(fin,r, a, b)
%bilateralFilter_rgb 彩色图像双边滤波
%   fout-滤波输出图像
%   fin-输入彩色图
%   r-滤波半径
%   a-全局标准差
%   b-局部标准差
%   双边滤波有两部分组成，一为空间权重:与像素位置有关(空域)，高斯滤波
%   另一为像素权重，与像素值(值域)大小有关，根据像素值大小不同而不同
%   空域滤波函数定义为c(x1, x2) = e^(-(x1.^2+x2.^2)/(2*a^2)),均值为0，标准差为a的高斯分布
%   值域滤波函数定义为s(y1, y2, y3) = e^(-(y1.^2+y2.^2+y3.^2)/(2*b^2)),   
%   其中y1、y2、y3分别表示三个通道上滤波器大小范围内像素值与中心像素的距离，均值为0，标准差为b的高斯分布

c = fspecial('gaussian', 2*r+1, a);  %空域滤波
fin = im2double(fin); %转double

h = waitbar(0,'Applying bilateral filter...');
set(h,'Name','Bilateral Filter Progress');

%分通道处理
fin_r = fin(:,:,1);
fin_g = fin(:,:,2);
fin_b = fin(:,:,3);
[m, n] = size(fin_r);

finRtemp = padarray(fin_r, [r,r], 'symmetric');
finGtemp = padarray(fin_g, [r,r], 'symmetric');
finBtemp = padarray(fin_b, [r,r], 'symmetric');

[fout_r, fout_g, fout_b] = deal(zeros(size(fin_r)));


for i = r+1:m+r
    for j = r+1:n+r
        temp1 = finRtemp(i-r:i+r, j-r:j+r);
        temp2 = finGtemp(i-r:i+r, j-r:j+r);
        temp3 = finBtemp(i-r:i+r, j-r:j+r);
        dr = temp1 - finRtemp(i,j);
        dg = temp2 - finGtemp(i,j);
        db = temp3 - finBtemp(i,j);
        s = exp(-(dr.^2+dg.^2+db.^2)/(2*b^2));
        w = c.*s;
        
        fout_r(i-r,j-r) = sum(sum(temp1.*w))/sum(w(:));
        fout_g(i-r,j-r) = sum(sum(temp2.*w))/sum(w(:));
        fout_b(i-r,j-r) = sum(sum(temp3.*w))/sum(w(:));
    end
    waitbar((i-r)/n);
end
fout = cat(3, fout_r, fout_g, fout_b); %得到输出

• 实验结果

原图	滤波半径5，全局标准差3，局部标准差0.1

联合双边滤波(上采样)

​ 在阅读CVPR2020论文《Underexposed Photo Enhancement using Deep Illumination Estimation》论文中采用联合双边滤波上采样(Joint bilateral-grid-based upsampling)技术来降低计算损失，这样做的目的是为了现将原图降采样到低分辨率，然后进行相关算法处理(省时)，然后利用联合双边滤波上采样方法来重建得到原始分辨率大小的图像，这种方法相对线性插值(linear)，最近邻插值(nearst)，三次立方插值(cubic)等取得更好的效果。

​ 当然文章中的联合双边滤波上采样也是用深度学习的方法来估算参数的，有兴趣可见论文《Deep Bilateral Learning for Real-Time Image Enhancement》，这里仅对联合双边滤波的原理进行介绍和实现。

​ 首先根据前面介绍的双边滤波公式可以表示为:
$$J_p=\frac{1}{k_p}\sum _{q\in \Omega }{I}_{q}f(||p-q||)g(||I_p-I_q)$$
其中$I$ 表示输入图像，$p、q$表示像素的空间位置，$I_p$表示对应位置的像素值，$J$表示输出，$f、g$分别表示空间权值分布函数和像素局部范围权值分布函数，均为高斯函数。这种滤波的结果就是周边像素的权值不仅和距离有关还和那个位置的像素值有关，如果在值域(range domain)的权值计算过程中引入另外一幅图像，如下式，则称为联合双边滤波。
$$J_p=\frac{1}{k_p}\sum _{q\in \Omega }{I}_{q}f(||p-q||)g(||\widetilde{I_p}-\widetilde{I_q})$$
联合双边滤波上采样技术也很简单，一种便于理解的也便于写代码的方式就是把下采样并进行处理过后的小图按照最近邻插值的方式放大到原图大小，然后再用原图的数据和这个放大的结果进行联合双边滤波处理。

可以参考文章：《Joint Bilateral Upsampling》

想比如上述那些复杂的算法，联合双边滤波的快速算法的耗时几乎可以忽略不计，如果一个算法下采样的采样率为0.25，则算法那本身的速度理想状态下可能只为原始的1/16，加上最后的联合双边滤波的时间，可能提高10倍以上，而效果变化并不大。

联合双边滤波实现

• matlab源码

function fout = JointBilaterFilterUp(src,ref,r,sigma)
%JointBilaterFilterUp 联合双边滤波上采样
%   fout-联合双边滤波输出图像
%   src-下采样后经过处理的图像
%   ref-原始图像，未经处理后的图像
%   r-滤波半径
%   sigma-全局标准差和局部标准差
%   参考来源:https://www.cnblogs.com/Imageshop/p/3677313.html
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Pre-process input and select appropriate filter.

% Verify that the input image exists and is valid.
if ~exist('src','var') || isempty(src) || ~exist('ref','var') || isempty(ref)
   error('Input image src or ref is undefined or invalid.');
end
if ~isfloat(src) || ~sum([1,3] == size(src,3)) || ...
      min(src(:)) < 0 || max(src(:)) > 1
   error(['Input image src must be a double precision ',...
          'matrix of size NxMx1 or NxMx3 on the closed ',...
          'interval [0,1].']);      
end
if ~isfloat(ref) || ~sum([1,3] == size(ref,3)) || ...
      min(ref(:)) < 0 || max(ref(:)) > 1
   error(['Input image ref must be a double precision ',...
          'matrix of size NxMx1 or NxMx3 on the closed ',...
          'interval [0,1].']);      
end

% Verify bilateral filter window size.
if ~exist('r','var') || isempty(r) || ...
      numel(r) ~= 1 || r < 1
   r = 5;
end
r = ceil(r);

% Verify bilateral filter standard deviations.
if ~exist('sigma','var') || isempty(sigma) || ...
      numel(sigma) ~= 2 || sigma(1) <= 0 || sigma(2) <= 0
   sigma = [3 0.1];
end

% Apply either grayscale or color bilateral filtering.
if size(src,3) == 1
   fout = jbfltGray(src,ref,r,sigma(1),sigma(2));
else %彩色图像
   fout = jbfltColor(src,ref,r,sigma(1),sigma(2));
end
end

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Implements bilateral filtering for grayscale images.
function fout = jbfltGray(src,ref,r,sigma_d,sigma_r)

% Pre-compute Gaussian distance weights.
[X,Y] = meshgrid(-r:r,-r:r);
G = exp(-(X.^2+Y.^2)/(2*sigma_d^2));

% Create waitbar.
%h = waitbar(0,'Applying bilateral filter on gray image...');
%set(h,'Name','Bilateral Filter Progress');


%resize src to ref image size
src = imresize(src, size(ref), 'bilinear');

% Apply bilateral filter.
[m, n] = size(src);
fout = zeros(size(src));
for i = 1:m
   for j = 1:n
         % Extract local region.
         iMin = max(i-r,1);
         iMax = min(i+r,m);
         jMin = max(j-r,1);
         jMax = min(j+r,n);
         I = src(iMin:iMax,jMin:jMax);
         
         % To compute weights from the ref image
         J = ref(iMin:iMax,jMin:jMax);
      
         % Compute Gaussian intensity weights according to the ref image
         H = exp(-(J-ref(i,j)).^2/(2*sigma_r^2));
      
         % Calculate bilateral filter response.
         F = H.*G((iMin:iMax)-i+r+1,(jMin:jMax)-j+r+1);
         fout(i,j) = sum(F(:).*I(:))/sum(F(:));
               
   end
   %waitbar(i/dim(1));
end

end
% Close waitbar.
%close(h);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Implements bilateral filtering for grayscale images.
function fout = jbfltColor(src,ref,r,sigma_d,sigma_r)

% Pre-compute Gaussian distance weights.
[X,Y] = meshgrid(-r:r,-r:r);
G = exp(-(X.^2+Y.^2)/(2*sigma_d^2));

% Create waitbar.
%h = waitbar(0,'Applying bilateral filter on gray image...');
%set(h,'Name','Bilateral Filter Progress');

%resize src to ref image size
[m, n, c] = size(ref);
src = imresize(src, [m, n], 'bilinear');

%分通道处理
src_r = src(:,:,1);
src_g = src(:,:,2);
src_b = src(:,:,3);

ref_r = ref(:,:,1);
ref_g = ref(:,:,2);
ref_b = ref(:,:,3);

%输出图像
[fout_r, fout_g, fout_b] = deal(zeros(size(src_r)));

% Apply bilateral filter.
for i = 1:m
   for j = 1:n
         % Extract local region.
         iMin = max(i-r,1);
         iMax = min(i+r,m);
         jMin = max(j-r,1);
         jMax = min(j+r,n);
         I_r = src_r(iMin:iMax,jMin:jMax);
         I_g = src_g(iMin:iMax,jMin:jMax);
         I_b = src_b(iMin:iMax,jMin:jMax);
         
         % To compute weights from the ref image
         J_r = ref_r(iMin:iMax,jMin:jMax);
         J_g = ref_g(iMin:iMax,jMin:jMax);
         J_b = ref_b(iMin:iMax,jMin:jMax);
         dr = J_r - ref_r(i, j);
         dg = J_g - ref_g(i, j);
         db = J_b - ref_b(i, j);
      
         % Compute Gaussian intensity weights according to the ref image
         H = exp(-(dr.^2+dg.^2+db.^2)/(2*sigma_r^2));
      
         % Calculate bilateral filter response.
         F = H.*G((iMin:iMax)-i+r+1,(jMin:jMax)-j+r+1);
         fout_r(i, j) = sum(sum(F.*I_r))/sum(F(:));
         fout_g(i, j) = sum(sum(F.*I_g))/sum(F(:));
         fout_b(i, j) = sum(sum(F.*I_b))/sum(F(:));
         %fout(i,j) = sum(F(:).*I(:))/sum(F(:));          
   end
   %waitbar(i/dim(1));
end
fout = cat(3, fout_r, fout_g, fout_b);
end

• 实验结果

去雾算法：

原图	下采样图然后应用去雾算法
最近邻插值	联合双边滤波

水下图像增强算法

原图(1024x768)	下采样并应用增强算法(256x256)
最近邻插值	联合双边滤波

在这个过程中参数的选取十分重要(按照经验 局部标准差一般取较小0.1，滤波半径和全局标准差取值较大30、30)，选取的不好效果就很差，而且不同类型的照片参数选取也存在差异，在实用中参数泛化能力不强，因此可以考虑结合深度学习的方法来学习参数。