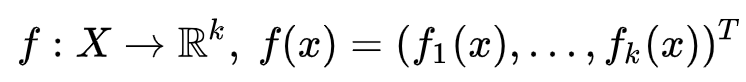多目标优化问题及求解
1。多目标优化问题定义
多目标优化是多准则决策的一个领域，它是涉及多个目标函数同时优化的数学问题。多目标优化已经应用于许多科学领域，包括工程、经济和物流，其中需要在两个或多个相互冲突的目标之间进行权衡的情况下作出最优决策。分别涉及两个和三个目标的多目标优化问题的例子有：在购买汽车时降低成本，同时使舒适性最大化；在使车辆的燃料消耗和污染物排放最小化的同时将性能最大化。在实际问题中，甚至可以有三多个目标。
对于非平凡多目标优化问题，不存在同时优化每个目标的单个解决方案。在这种情况下，目标函数被说成是冲突的，并且存在一个（可能无限）数量的帕累托最优解。如果目标函数在值上不能改进而不降低其他一些目标值，则解决方案称为非支配、Pareto最优、Pareto有效或非劣解。如果没有额外的主观偏好信息，所有Pareto最优解都被认为是同样好的（因为向量不能完全排序）。研究人员从不同的角度研究多目标优化问题，从而在设置和解决多目标优化问题时存在不同的求解哲学和目标。目标可以是找到帕累托最优解的代表性集合，and/or量化满足不同目标的折衷，and/or找到满足人类决策者decision maker(DM)的主观偏好的单一解决方案。
介绍： 多目标优化问题是一个涉及多目标函数的优化问题。在数学术语中，可将多目标优化问题化为：
其中整数K>= 2是目标数，并且集合 X是可行的决策向量集。可行集通常由一些约束函数定义。此外，向量值目标函数通常定义为
帕累托 (Pareto) 前沿（红色）的例子，帕累托最优解的集合（那些没有被任何其他可行解支配的）。点C不在帕累托边界上，因为它由点A和点B共同支配。点A和B不由任何其他点支配，且不互相支配。像A、B这类解就是多目标优化问题的可执行解，也被称为Pareto最优解。在多目标优化过程中，通常不存在同时最小化所有目标函数的可行解。因此，帕累托最优解；即，在不降低至少一个其他目标的情况下，任何目标都不能改进的解。这些Pareto最优解组成的集合便是最优解集合。
【来源：web； URL：https://en.wikipedia.org/wiki/Multi-objective_optimization 】
2. 发展历史
描述
理性的人们试图在一组可能的选择中做出“最优”的决定。然而实际上，“最优”这个名词在不同的领域中被赋予不同意义。在经济学中，“最优”指买方和卖方（微观经济学）或政府（宏观经济学），同时优化或平衡若干标准的决策。税收就是一个很好的例子。一个最佳的，平均的税收水平（每美元的经济活动）最大限度地提高了可用于公共利益的收入，同时保持了足够的激励，个人从自己的工作中赚取收入。第一个考虑这种权衡的人是F. Y Edgeworth。
1881年，在伦敦国王学院（King's College）和之后是在牛津大学（Oxford）的经济学教授 F.Y.Edgeworth 是第一个为多准则经济决策制定最佳方案的人（Edgeworth 1881）。他在两个假设的消费者准则P和π的背景下针对多效用问题做了这样定义：“需要找到一个点（x，y），这样无论我们朝哪个方向迈出无穷小的一步，P和π不会一起增加，而是一个增加，另一个减少。
1893年，帕雷托成为瑞士洛桑大学政治经济学的主席，在那里他创立了两个最著名的理论：精英的流通和帕雷托最优（Circulation of the Elites and The Pareto Optimum）。虽然第一种观点至今仍存在争议，但第二种观点已得到广泛接受(Pareto 1906)：“只要能够使至少一个人在他自己的估计中过得更好，社会资源的最佳分配就不可能实现。像以前一样保持别人的自我评价。
另一个活动和进展的热点是日本，特别是在多目标优化的理论方面（Sawaragi，Nakayama和Tanino，1985）。 在过去的三十年中，多目标优化的应用在工程和设计的许多领域中稳步增长。 互联网的出现以及关于该主题的一些重点会议也促成了多目标优化的研究人员和从业者社区的形成。 该领域的一个特别值得注意的资源是由（Coello-Coello 2004）创建和维护的网站。
各种多目标优化算法也是应运而生，Scalarization Methods （如，Andersson 2001）；Pareto Methods；Hybrid methods（Miettinen, K，2008）。
多目标优化算法归结起来有传统优化算法和智能优化算法两大类。
- 传统优化算法包括加权法、约束法和线性规划法等，实质上就是将多目标函数转化为单目标函数，通过采用单目标优化的方法达到对多目标函数的求解。
- 智能优化算法包括进化算法（Evolutionary Algorithm, 简称EA）、粒子群算法（Particle Swarm Optimization, PSO）等。
从九十年代初开始，进化算法系列算法被统一，如遗传算法（GA）等。进化算法的应用范围很广。
2002年，Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. A. M. T应用遗传算法来解决多目标优化问题。优化问题也是进化算法最擅长解的问题之一。
2009年，Liang等学者针对PSO算法应用在多模态问题（multimodal problem）时容易陷入局部最优解的问题，提出了CLPSO（comprehensive learning particle swarm optimizer）算法来防止算法过早收敛（pre-convergence）。
【Evolutionary computation/algorithm - Yuanyuan LI】https://www.jiqizhixin.com/graph/technologies/fd0fb517-7786-4fe0-99d3-170d849cdf12
2018年，在NIPS上的《Multi-task learning as multi-objective optimization》明确将多任务学习视为多目标优化问题，以寻求帕累托最优解。Sener, O., & Koltun, V.提出的方法可以在现实假设下得到帕累托最优解。
【出处：paper，http://strategic.mit.edu/docs/3_46_CJK-OSM3-Keynote.pdf 】
主要事件
| 年份 | 事件 | 相关论文 |
| 1906 | Pareto提出核心思想 | Pareto, V. (1906). Manuale di economia politica (Vol. 13). Societa Editrice. |
| 1979 | Stadler, W. 对帕累托最优进一步回顾 | Stadler, W. (1979). A survey of multicriteria optimization or the vector maximum problem, part I: 1776–1960. Journal of Optimization Theory and Applications, 29(1), 1-52. |
| 2008 | Miettinen, K.提出一种混合方法解决多目标问题 | Miettinen, K., Ruiz, F., & Wierzbicki, A. P. (2008). Introduction to multiobjective optimization: interactive approaches. In Multiobjective Optimization (pp. 27-57). Springer, Berlin, Heidelberg. |
| 2014 | Deb, K.对多目标优化进行回顾 | Deb, K. (2014). Multi-objective optimization. In Search methodologies (pp. 403-449). Springer, Boston, MA. |
| 2018 | Sener, O., & Koltun, V.提出多任务学习来作为多目标优化的策略 | Sener, O., & Koltun, V. (2018). Multi-task learning as multi-objective optimization. In Advances in Neural Information Processing Systems (pp. 524-535). |
3. 发展分析
瓶颈
多目标优化算法相对成熟，在不同的问题使用不同的优化算法。NSGA-II, SPEA 或者 MOPSO都是可选项，而到底选择哪一个方法，还需要根据特定的情景选择。
尽管多目标优化算法应用于动态的制造系统（Dynamic Manufacturing Systems），但是制造系统的复杂特性，使得算法仍然需要完善。
未来发展方向
1.因为多种多目标方法已经被提出，混合方法 hybrid method可以被进一步发展。
2. 现在的动态制造系统中的多目标优化算法需要动态调度的能力
【 https://ieeexplore.ieee.org/document/4667864 】