计量模型 | 时间固定效应与时间趋势项
这期推送将比较时间固定效应和时间趋势项的区别,并使用两种方法对模型中可能存在的trend进行识别。
N o t e : Note: Note: 1、该文首发于微信公众号
DMETP,欢迎关注;2、需要本次推送所使用的数据和代码的朋友,可以在公众号后台对话框内回复关键词trend。
一、时间FE & 时间trend
在LSDV法下,时间固定效应(time FE)表现为一系列的时间虚拟变量,对于特定年份 y e a r ∗ year^* year∗,若样本所处年份是 y e a r ∗ year^* year∗则记为1,否则记为0。在Stata中,这一系列的时间虚拟变量引入方式有两种:
- 一是直接在回归命令中加入类别变量,如
i.year,使用这种方式无需生成额外的变量,节约内存。 - 二是生成额外的时间虚拟变量并加入回归命令中,如先
tabulate year, gen(fe_),然后在回归命令中写入fe_*。
控制时间FE的用意在于吸收时间维度上不可观测的同质性冲击的影响,即所有个体共有的时间因素,如宏观经济冲击、财政货币政策等等,假定这些因素在特定年份对不同个体的影响是一致的。此外,如果考虑到异质性,即考虑到这些因素可能对不同组别(如省、城市、行业等)的个体影响不一致,则可以在模型中引入交互FE,如行业-时间FE。这种交互FE在reghdfe命令下有两种引入方式(以行业-时间FE为例):
- 一是首先
egen ind_year = group(ind year),其次在reghdfe命令的选择项中写入absorb(ind_year)。 - 二是使用因子表达式直接在选择项中写入,如
absorb(ind#year)。
模型引入时间趋势项(time trend)一般有三种方法:
- 法一:直接在回归命令中写入
c.year或year。 - 法二:假设样本数据集(而不是各个样本!)的最小年份为
year_min,则首先生成trend = year - year_min + 1,然后再在模型中引入trend。 - 法三:首先
bysort id (year): gen trend = _n,其中,(year)是为了保证样本按照id - year进行升序排序。其次再在回归命令中写入trend。
推文利用法三生成trend,法三的缺陷在于,如果样本存续年份中断,如2012、2014、2018,法三将视这三年为连续年份,并分别记为1、2、3。
加入时间趋势项是为了控制不同个体的被解释变量可能存在的并且尚未被其他控制变量和FE所覆盖/解释的增减趋势,因为不同组别(规模、性质、政策分组、生命周期等)个体的被解释变量的时间趋势或许存在一定程度的差异,并且在控制已有的解释变量之后依然可能存在较为明显的时间趋势。
以上内容可总结为以下几点:
- 第一,在
LSDV法下时间FE为一系列的虚拟变量,而时间trend为一个变量。 - 第二,时间FE用来吸收不随个体但随时间而变的不可观测因素冲击的影响,而时间trend则用来控制被解释变量可能存在的增减趋势。
- 第三,时间FE本质上是包括trend了的,trend可由FE线性表出,因此如果在方程中同时加入FE和trend,trend可能由于出现多重共线性而被omitted,但是两者同时加入模型可使得估计结果更稳健
- 第四,在整体序列较长的长面板中,很大可能需要控制时间trend对回归结果的影响。
二、时间trend的识别
下面将对模型中可能存在的时间趋势进行识别,推文提供两种思路:
- 一是直接在回归模型中加入trend,如果trend不显著,说明不需要引入。
- 二是在控制除trend外所有的变量及FE后,观察残差中是否仍旧存在trend,如果存在,说明被解释变量的增减趋势不能完全被变量和FE所吸收,模型须额外引入trend。
根据以上两种识别思路设计出两种识别方法:一是回归法,二是图形法。
2.1 回归法
vers 17
copy https://www.stata-press.com/data/r17/nlswork.dta nlswork.dta, replace
clear all
use nlswork.dta, clear
xtset idcode year
gl regst "qui reghdfe ln_w grade age c.age#c.age ttl_exp c.ttl_exp#c.ttl_exp tenure c.tenure#c.tenure not_smsa south"
gl regopt "absorb(idcode year) resid"
********************************************************************************
**# 生成时间趋势项
bys idcode (year): gen t = _n
* gen t = year
* gen t = year - 67 // 另外两种 t 的生成方法
********************************************************************************
**# 法一:回归
$regst t, $regopt
dis "系数(Total) = " %6.4f _b[t] ";t值(Total) = " %6.4f _b[t] / _se[t]
$regst t if race == 1, $regopt
dis "系数(White) = " %6.4f _b[t] ";t值(White) = " %6.4f _b[t] / _se[t]
$regst t if race != 1, $regopt
dis "系数(Other) = " %6.4f _b[t] ";t值(Other) = " %6.4f _b[t] / _se[t]
运行以上代码可以观察到,无论是在总体样本、白人群体还是其他人种群体,时间趋势项t的回归系数均不显著(5%的显著水平下),且系数大小接近于0,这说明原模型中无须引入trend,trend对回归结果的干扰较小。
2.2 图形法
**# 法二:画图
frame dir
frame rename default a
frame copy a b
frame a {
$regst , $regopt
predict r, resid
drop if mi(r)
gcollapse (mean) r_mean = r (sd) r_sd = r, by(t)
gen upper = r_mean + 1.65 * r_sd
gen lower = r_mean - 1.65 * r_sd
gen race1 = 2
}
frame b {
gen race1 = (race == 1)
$regst if race1, $regopt
predict r, resid
$regst if !race1, $regopt
predict r1, resid
replace r = r1 if !race1
drop if mi(r)
gcollapse (mean) r_mean = r (sd) r_sd = r, by(race1 t)
gen upper = r_mean + 1.65 * r_sd
gen lower = r_mean - 1.65 * r_sd
}
frame a {
frameappend b
label define race 0 "Other" 1 "White" 2 "Total"
label values race1 race
#d ;
twoway (con r_mean t, m(o))
(rcap upper lower t, msiz(vsmall)),
yline(0 , lc(red))
by(race1, note("") rows(1))
legend(label(1 "Mean of residuals")
label(2 "90% confidence interval"))
xlabel(, labs(medsmall) format(%4.0f))
ylabel(, labs(medsmall) format(%4.1f))
xtitle("Trend") ytitle("Residuals")
scheme(qleanmono)
saving(time_trend, replace)
;
#d cr
graph export "time_trend.emf", replace
}
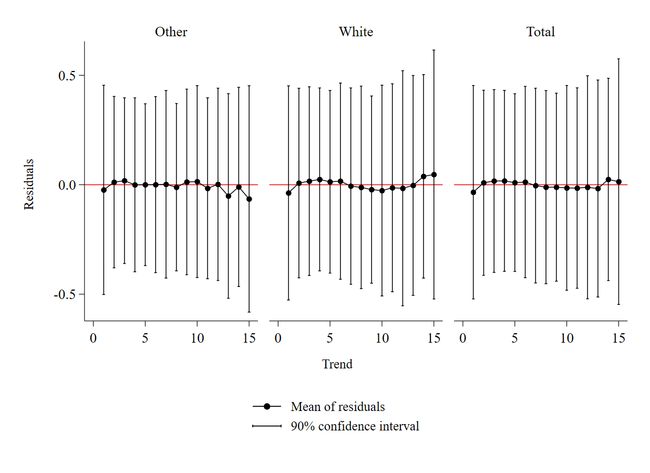
以上代码的运行结果如图 1。
观察图 1可知,无论是总体、白人群体还是其他人种群体样本,回归残差的均值均在0值附近上下波动,90%的置信区间跨越了0值线,并且随着时间趋势的推移,残差均值并未表现出明显的增减趋势,这些都同样说明了原模型中无须引入trend,trend对回归结果的干扰较小。