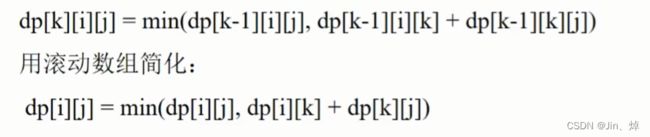蓝桥杯第16天（Python版）（图论）

1. 最大降雨量

 问题是求中位数的中位数，上面解题思路图便于理解

import os
import sys

# 请在此输入您的代码
# 降雨量为 7 周能量的中位数。
#1-7
#8-14
#15-21
#22-28
#29-35
#36-42
#43-49
#22-49 =28
# 后面28天尽可能的相同，这样中位数才能大


# 22+49 23+48  24+47  34
# 25+46 26+45  27+44  35
# 28+43 29+42  30+41  36
# 31+40 32+39  33+38  37

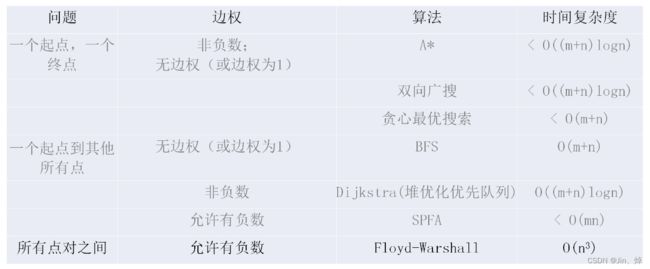
print(34)

2.最短路算法比较

3.Floyd算法 （多对多，可以简化成一对多或者多对一）

动态规划 ，原理

 计算过程，结合图形理解

 计算步骤（将k从1扩展到n）

 数组滚动简化方程 （细看，k只用到了上一层，所以可以简化，直接舍去不要）

def floyd():
    global dp
    for k in range(1,n+1):
        for i in range(1,n+1):
            for j in range(1,n+1):
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
dp = [[99999999 for _ in range(N) for _ in range(N)]  #dp[i,j]表示i到j最短路径

Floyd例题1

两种写法

import math
def floyd():
    global dp
    for k in range(1,2022):
        #for i in range(1,2022):
        for i in range(1,2):
            for j in range(1,2022):
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])
dp = [[9999999999 for _ in range(2022)] for _ in range(2022)]  #dp[i,j]表示i到j最短路径

for i in range(1,2022):
    for j in range(1,2022):
        if abs(i-j)<=21:
            dp[i][j]=i//math.gcd(i,j)*j
floyd()
print(dp[1][2021])

from math import gcd
def lcm(x,y):
    return x//gcd(x,y)*y
dp = [9999999999]*2022      # 点i到1的最短路径
dp[1]=0  #到自身的距离为0
for i in range(1,2022):  # 1-2022
    for j in range(i+1,i+22):  #和i有边的点j
        if j>2021:
            break
        dp[j] = min(dp[j],dp[i]+lcm(i,j)) # 更新最短路

print(dp[2021])

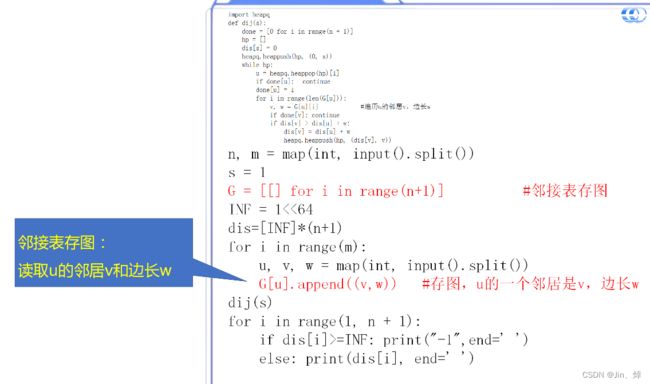
4.Dijkstra

算法实现

 

举例说明：

 

 

 

 例题：