12、Go语言数据结构
目录
- 一、链表
-
- 1 - 单向链表
- 2 - 双向链表
- 3 - 双向循环链表
- 二、栈
- 三、堆
-
- 1 - 堆的概念
- 2 - 堆的应用
- 3 - 堆的实现
一、链表
1 - 单向链表
- 单向链表
package main
import "fmt"
type Node struct {
Info int
Next *Node
}
type List struct {
Head *Node
Len int
}
func (list *List) Add(ele int) {
node := &Node{Info: ele, Next: nil}
if list.Len == 0 {
list.Head = node
} else {
curNode := list.Head
for i := 0; i < list.Len-1; i++ {
curNode = curNode.Next
}
curNode.Next = node
}
list.Len += 1
}
func (list List) Travs() {
if list.Len == 0 {
return
}
curNode := list.Head
fmt.Printf("%d ", curNode.Info)
for i := 0; i < list.Len-1; i++ {
curNode = curNode.Next
fmt.Printf("%d ", curNode.Info)
}
fmt.Println()
}
func main() {
list := List{}
list.Add(1)
list.Add(3)
list.Add(5)
list.Add(7)
list.Travs() //1 3 5 7
}
- 效率优化：上面的例子我们可以看到，每添加一个元素需要遍历整个链表；如果我们在List也保存最后一个Node的信息，就不需要遍历整个链表
package main
import "fmt"
type Node struct {
Info int
Next *Node
}
type List struct {
Head *Node
Len int
Tail *Node
}
func (list *List) Add(ele int) {
node := &Node{Info: ele, Next: nil}
if list.Len == 0 {
list.Head = node
list.Tail = node
} else {
list.Tail.Next = node
list.Tail = node
}
list.Len += 1
}
func (list List) Travs() {
if list.Len == 0 {
return
}
curNode := list.Head
fmt.Printf("%d ", curNode.Info)
for i := 0; i < list.Len-1; i++ {
curNode = curNode.Next
fmt.Printf("%d ", curNode.Info)
}
fmt.Println()
}
func main() {
list := List{}
list.Add(1)
list.Add(3)
list.Add(5)
list.Add(7)
list.Travs() //1 3 5 7
}
2 - 双向链表
- go语言中自带的双向链表：
container/list
func TravsList(lst *list.List) {
cur := lst.Front()
for cur.Next() != nil {
fmt.Printf("%v ", cur.Value)
cur = cur.Next()
}
fmt.Printf("%v", cur.Value)
fmt.Println()
}
func main() {
list := list.New() //创建一个空的双向链表
list.PushBack(4)
list.PushBack(6)
list.PushBack(2) //往链表尾部添加2
list.PushFront(9) //往链表头部添加9
TravsList(list) //9 4 6 2
}
- 链表的应用：LRU(Least Recently Used, 最近最少使用)，缓存淘汰的总体思路 -> 缓存的key放到链表中，头部的元素表示最近刚使
- 如果命中缓存，从链表中找到对应的key，移到链表头部
- 如果没命中缓存：
- 如果缓存容量没超，放入缓存，并把key放到链表头部
- 如果超出缓存容量，删除链表尾部元素，再把key放到链表头部
- 实现链表访问后将访问的元素移动到链表头部
package main
import "fmt"
type Node struct {
Info int
Next *Node
Pref *Node
}
type List struct {
Head *Node
Len int
Tail *Node
}
func (list *List) Add(ele int) {
node := &Node{Info: ele, Next: nil}
if list.Len == 0 {
list.Head = node
list.Tail = node
} else {
list.Tail.Next = node
node.Pref = list.Tail
list.Tail = node
}
list.Len += 1
}
func (list List) Travs() {
if list.Len == 0 {
return
}
curNode := list.Head
fmt.Printf("%d ", curNode.Info)
for i := 0; i < list.Len-1; i++ {
curNode = curNode.Next
fmt.Printf("%d ", curNode.Info)
}
fmt.Println()
}
func (list *List) Visit(ele int) {
if list.Len == 0 {
return
}
curNode := list.Head
for {
if curNode == nil {
break
}
if curNode.Info != ele {
curNode = curNode.Next
} else {
break
}
}
if curNode == nil {
return
} else {
prefNode := curNode.Pref
nextNode := curNode.Next
if nextNode == nil { //需要考虑curNode是最后一个node的情况
prefNode.Next = nil
} else {
prefNode.Next = nextNode
nextNode.Pref = prefNode
}
curNode.Next = list.Head
list.Head.Pref = curNode
list.Head = curNode
}
}
func main() {
list := List{}
list.Add(1)
list.Add(3)
list.Add(5)
list.Add(7)
list.Travs() //1 3 5 7
list.Visit(3)
list.Visit(7)
list.Travs() //7 3 1 5
}
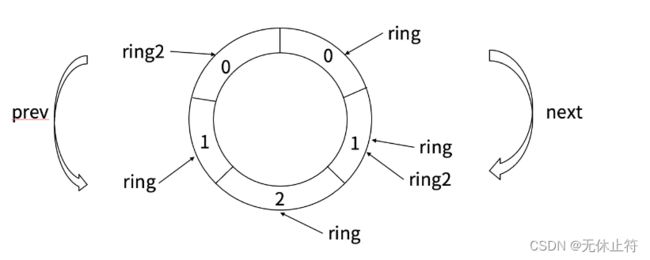
3 - 双向循环链表
- container/ring：双向循环链表
- ring的应用
- 基于滑动窗口的统计：比如最近100次接口调用的平均耗时、最近10笔订单的平均值、最近30个交易日股票的最高点
- ring的容量即为滑动窗口的大小，把待观察变量按时间顺序不停地写入ring即可
func RingDemo() {
r := ring.New(10) //容量是不可扩展的
for i := 0; i < 100; i++ {
r.Value = i
r = r.Next()
}
sum := 0
r.Do(func(i any) { //ring.Do遍历整个环，每个元素赋予func(i any)中的i
fmt.Printf("%v ", i)
num := i.(int)
sum += num
})
fmt.Println() //90 91 92 93 94 95 96 97 98 99
fmt.Println(sum) //945
}
二、栈
- 斐波那契数列递归造成的计算浪费：下面说明重复计算了多个3和2个递归
- 计算5的递归的时候，需要计算4的递归和3的递归
- 计算4的递归的时候，需要计算3的递归和2的递归
- 计算3的递归的时候，需要计算2的递归和1的递归
- 用栈解除递归：从运行结果可以看到非递归的时间复杂度远低于递归的时间复杂度
package main
import (
"container/list"
"fmt"
)
var (
n1 = 0 //记录递归的时间复杂度
n2 = 0 //记录非递归的时间复杂度
stack *list.List //stack只是我们自己的命令，不是栈，只是List实现了栈的功能
)
func init() {
stack = list.New()
}
func FibonacciWithRecursion(n int) int {
if n == 1 || n == 2 {
return n - 1
}
n1++
return FibonacciWithRecursion(n-1) + FibonacciWithRecursion(n-2)
}
func FibonacciWithStack(n int) int {
if n == 1 || n == 2 {
return n - 1
}
stack.PushBack(0)
stack.PushBack(1)
for i := 2; i < n; i++ {
a := stack.Back() //弹出栈顶的2个元素，分别赋给a和b
stack.Remove(a) //从链表上删除一个元素的时间复杂度为O(1)
b := stack.Back()
stack.Remove(b)
stack.PushBack(a.Value.(int)) //依次压入a和a+b
stack.PushBack(a.Value.(int) + b.Value.(int))
n2 += 5 //2次pop，2次push，1次加法
}
a := stack.Back()
result := stack.Remove(a)
n2 += 4 //2次pop，2次push
return result.(int)
}
func main() {
n := 20
fmt.Println(FibonacciWithRecursion(n)) //4181
fmt.Println(FibonacciWithStack(n)) //4181
fmt.Println(n1) //6764
fmt.Println(n2) //94
}
- 使用切片实现栈
type Stack struct {
slc []int
len int
cap int
}
func NewStack(n int) *Stack {
slc := make([]int, n)
return &Stack{
slc: slc,
len: 0,
cap: n,
}
}
func (stack *Stack) Push(ele int) error {
if stack.len >= stack.cap {
return errors.New("stack already full")
}
stack.slc[stack.len] = ele
stack.len += 1
return nil
}
func (stack *Stack) Pop() (int, error) {
if stack.len == 0 {
return 0, errors.New("stack is empty")
}
top := stack.slc[stack.len-1]
stack.len -= 1
return top, nil
}
func main() {
stack := NewStack(5)
stack.Push(1)
stack.Push(2)
stack.Push(3)
stack.Push(4)
stack.Push(5)
fmt.Println(stack.Push(6)) //stack already full
n, err := stack.Pop()
fmt.Println(n, err) //5 三、堆
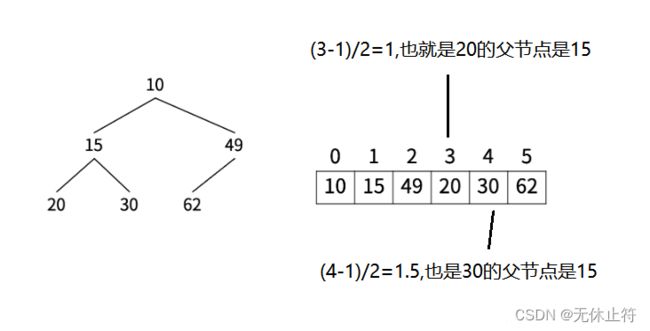
1 - 堆的概念
- 堆的底层表示：堆是一棵二叉树
- 大根堆即任意节点的值都大于等于其子节点。反之为小根堆
- 用数组来表示堆，下标为 i 的结点的父结点下标为(i-1)/2，其左右子结点分别为 (2i + 1)、(2i + 2)
2 - 堆的应用
-
堆的应用
- 堆排序：构建堆O(n)、不断的删除堆顶O(N*LogN)
- 求集合中最大的K个元素：
- 用集合的前K个元素构建小根堆
- 逐一遍历集合的其他元素，如果比堆顶小直接丢弃；否则替换掉堆顶，然后向下调整堆
- 超时缓存：把超时的元素从缓存中删除
- 按key的到期时间把key插入小根堆
- 周期扫描堆顶元素，如果它的到期时间早于当前时刻，则从堆和缓存中删除，然后向下调整堆
-
堆的构建
-
删除堆顶
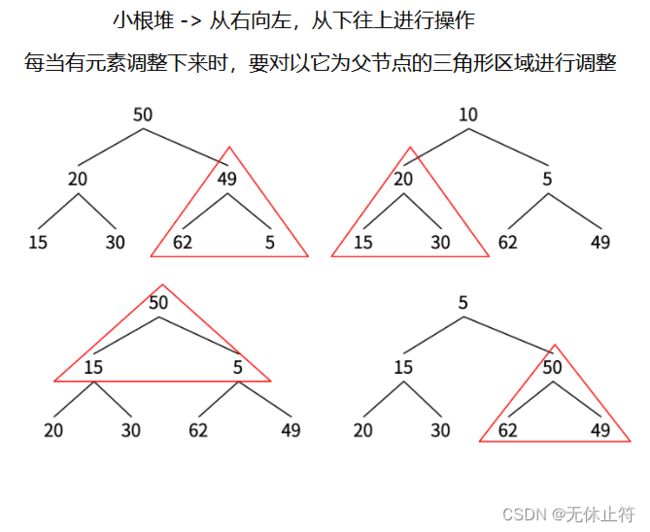
3 - 堆的实现
- golang中的堆：golang中的container/heap实现了小根堆，但需要自己定义一个类，实现以下接口
Len() intLess(i, j int) boolSwap(i, j int)Push(x interface{})Pop() x interface{}
package main
import (
"container/heap"
"fmt"
)
type Item struct {
Value string
priority int //优先级，数字越大，优先级越高
}
type PriorityQueue []*Item //优先级队列
func (pq PriorityQueue) Len() int {
return len(pq)
}
func (pq PriorityQueue) Less(i, j int) bool {
return pq[i].priority > pq[j].priority //golang默认提供的是小根堆，而优先队列是大根堆，所以这里要反着定义Less
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
}
// 往slice里append,需要传slice指针
func (pq *PriorityQueue) Push(x interface{}) {
item := x.(*Item)
*pq = append(*pq, item)
}
// 让slice指向新的子切片，需要传slice指针
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1] //数组最后一个元素
*pq = old[0 : n-1] //子切片截取操作，去掉最一个元素
return item
}
func testPriorityQueue() {
pq := make(PriorityQueue, 0, 10)
pq.Push(&Item{"A", 3}) //往数组里面添加元素
pq.Push(&Item{"B", 2})
pq.Push(&Item{"C", 4})
heap.Init(&pq) //根据数组中的元素构建堆
heap.Push(&pq, &Item{"D", 6}) //通过heap添加元素
for pq.Len() > 0 {
fmt.Printf("%v ", heap.Pop(&pq)) //通过heap删除堆顶元素
}
}
func main() {
testPriorityQueue() //&{D 6} &{C 4} &{A 3} &{B 2}
}