对称二叉树

1题目

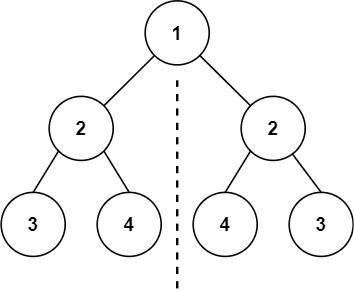
给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]

输出：true

示例 2：

输入：root = [1,2,2,null,3,null,3]

输出：false

2链接

题目：

视频：新学期要从学习二叉树开始！ | LeetCode：101. 对称二叉树_哔哩哔哩_bilibili

3解题思路

3.1递归法

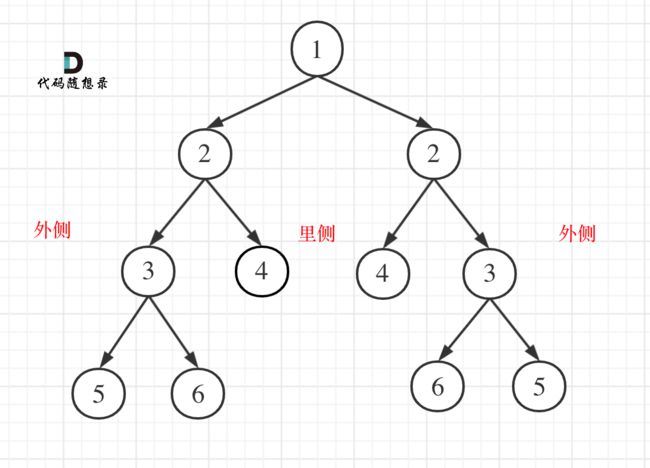
对于二叉树是否对称，要比较的是根节点的左子树与右子树是不是相互翻转的，理解这一点就知道了其实我们要比较的是两个树（这两个树是根节点的左右子树），所以在递归遍历的过程中，也是要同时遍历两棵树。

比较的是两个子树的里侧和外侧的元素是否相等。如图所示：

本题遍历只能是广义上的“后序遍历”，因为我们要通过递归函数的返回值来判断两个子树的内侧节点和外侧节点是否相等。

正是因为要遍历两棵树而且要比较内侧和外侧节点，相同后才能继续向上比较，所以准确的来说是一个树的遍历顺序是左右中，一个树的遍历顺序是右左中。

注意递归三部曲的写法：

1. 确定递归函数的参数和返回值

因为我们要比较的是根节点的两个子树是否是相互翻转的，进而判断这个树是不是对称树，所以要比较的是两个树，参数自然也是左子树节点和右子树节点。

返回值自然是bool类型。

bool compare(TreeNode* left, TreeNode* right)

2. 确定终止条件

节点为空的情况有：（注意我们比较的其实不是左孩子和右孩子，所以如下我称之为左节点右节点）

• 左节点为空，右节点不为空，不对称，return false

• 左不为空，右为空，不对称 return false

• 左右都为空，对称，返回true

此时已经排除掉了节点为空的情况，那么剩下的就是左右节点不为空：

• 左右都不为空，比较节点数值，不相同就return false

此时左右节点不为空，且数值也不相同的情况我们也处理了。

if (left == NULL && right != NULL) return false;
else if (left != NULL && right == NULL) return false;
else if (left == NULL && right == NULL) return true;
else if (left->val != right->val) return false; // 注意这里我没有使用else

3. 确定单层递归的逻辑

此时才进入单层递归的逻辑，单层递归的逻辑就是处理 左右节点都不为空，且数值相同的情况。

• 比较二叉树外侧是否对称：传入的是左节点的左孩子，右节点的右孩子。

• 比较内测是否对称，传入左节点的右孩子，右节点的左孩子。

• 如果左右都对称就返回true ，有一侧不对称就返回false 。

bool outside = compare(left->left, right->right);   // 左子树：左、 右子树：右
bool inside = compare(left->right, right->left);    // 左子树：右、 右子树：左
bool isSame = outside && inside;    // 左子树：中、 右子树：中（逻辑处理）
return isSame;

如上代码中，我们可以看出使用的遍历方式，左子树左右中，右子树右左中，所以我把这个遍历顺序也称之为“后序遍历”（尽管不是严格的后序遍历）。

3.2迭代法

注意，这里的迭代法可不是前中后序的迭代写法，因为本题的本质是判断两个树是否是相互翻转的，其实已经不是所谓二叉树遍历的前中后序的关系了。

这里我们可以使用队列来比较两个树（根节点的左右子树）是否相互翻转，（注意这不是层序遍历）

通过队列来判断根节点的左子树和右子树的内侧和外侧是否相等，如动画所示：

条件判断和递归的逻辑是一样的。

这个迭代法，其实是把左右两个子树要比较的元素顺序放进一个容器，然后成对成对的取出来进行比较，那么其实使用栈也是可以的。只要把队列原封不动的改成栈就可以了

4代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
//递归法——广义上的后序遍历
class Solution {
public:
    bool compare(TreeNode* left, TreeNode*right) {
        // 首先排除空节点的情况
        if (left == nullptr && right != nullptr) return false;
        else if (left != nullptr && right == nullptr) return false;
        else if (left == nullptr && right == nullptr) return true;
        // 排除了空节点，再排除数值不相同的情况
        else if (left->val != right->val) return false;
        // 此时就是：左右节点都不为空，且数值相同的情况，开始递归，做下一层的判断
        bool outside = compare(left->left, right->right);// 左子树：左、 右子树：右
        bool inside = compare(left->right, right->left);// 左子树：右、 右子树：左
        bool result = outside && inside;// 左子树：中、 右子树：中 （逻辑处理）
        //可以这么简写
        //else return compare(left->left, right->right) && compare(left->right, right->left);
        return result;
    }
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return root;
        else return compare(root->left, root->right);
    }
};

//迭代法——使用队列
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return true;
        queue que;
        que.push(root->left); // 将左子树头结点加入队列
        que.push(root->right); // 将右子树头结点加入队列
        while (!que.empty()) { // 判断这两个树是否相互翻转
            TreeNode* leftNode = que.front();
            que.pop();
            TreeNode* rightNode = que.front();
            que.pop();
            // 左节点为空、右节点为空，此时说明是对称的，不能返回false要继续while循环
            if (!leftNode && !rightNode) continue;
            // 左右一个节点不为空，或者都不为空但数值不相同，返回false
            if ((!leftNode || !rightNode) || (leftNode->val != rightNode->val)) {
                return false;
            }
            que.push(leftNode->left);// 加入左节点左孩子
            que.push(rightNode->right);// 加入右节点右孩子
            que.push(leftNode->right);// 加入左节点右孩子
            que.push(rightNode->left);// 加入右节点左孩子
        }
        return true;
    }
};

//迭代法——使用栈
class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if (root == nullptr) return root;
        stack st; //队列换成了栈
        st.push(root->left); //如果先加左子树
        st.push(root->right); //后加右子树
        while (!st.empty()) {
            TreeNode* rightNode = st.top(); //第一个栈顶就是加进来的右子树
            st.pop();//弹出栈顶元素
            TreeNode* leftNode = st.top();//第二个栈顶就是加进来的左子树
            st.pop();
            if (!leftNode && !rightNode) continue;
            if ((!leftNode || !rightNode) || (leftNode->val != rightNode->val)) {
                return false;
            }
            st.push(leftNode->left);
            st.push(rightNode->right);
            st.push(leftNode->right);
            st.push(rightNode->left);
        }
        return true;
    }
};