LeetCode 189. 轮转数组

前言

Wassup guys！我是Edison

今天是 LeetCode 上的 leetcode 189. 轮转数组

Let’s get it！

---

---

1. 题目分析

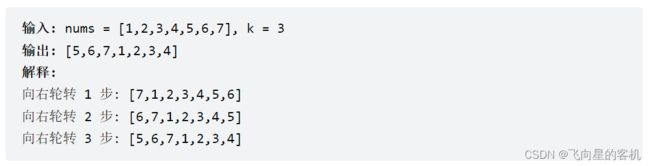
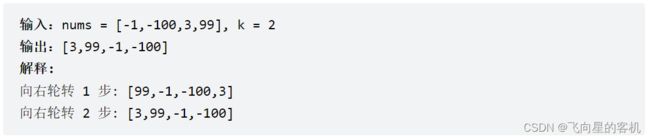
给你一个数组，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例 1：

示例 2：

2. 题目图解

思路一：右旋 k 次，依次移动一个

假设我们要把数组 [1，2，3，4，5，6，7]，向右旋转 3 次

第 1 步，定义一个变量 tmp 用于存放数组的最后一个元素 7；

第 2 步，把数组前 n-1 个值往后挪；

第 3 步，把 tmp 的值放入空出来的第一个位置中；

这就完成了一次右旋，那么我们在向右旋转 k 次，就得到了最后的结果。

此方法时间复杂度为 $O(N\ast K)$；空间复杂度为 $O(1)$；
 
当 K % N 等于 N-1 时，最坏，因为此时时间复杂度为 $O(N^2)$；

思路二：额外开数组

这种方法是以 空间换时间 的做法。

很简单，再开辟一个数组，把后 k 个元素放到新数组 前面，再把前 n-k个放到新数组 后面。（n 为数组中的元素个数）。

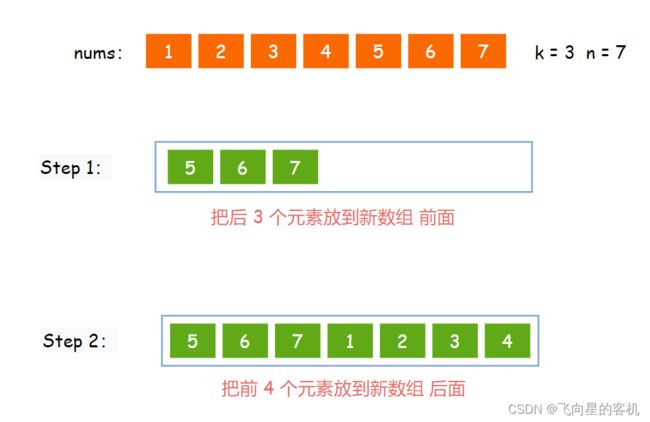
此方法时间复杂度为 $O(N)$，空间复杂度为 $O(N)$

思路三：三趟逆置

这种方法非常的 绝！，我们可以通过 三趟逆置 来解决，还是下面这个数组

第 1 趟，对数组的前 n - k 个逆置，如图所示

第 2 趟，对数组的后 k 个逆置，如图所示

第 3 趟，再把数组 整体逆置，如图所示

此方法时间复杂度为 $O(N)$，空间复杂度为 $O(1)$。

3. 算法设计

我们可以写一个 逆置 函数 reverse 来实现主要部分

代码实现

void reverse(int* nums, int left, int right) {
	while (left < right) {
		int tmp = nums[left];
		nums[left] = nums[right];
		nums[right] = tmp;
		++left;
		--right;
	}
}

4. 代码实现

我们使用逆置函数 reverse 进行传参的时候要注意：数组的下标是从 0 开始的，比如：前 10 个元素是 0 到 9；

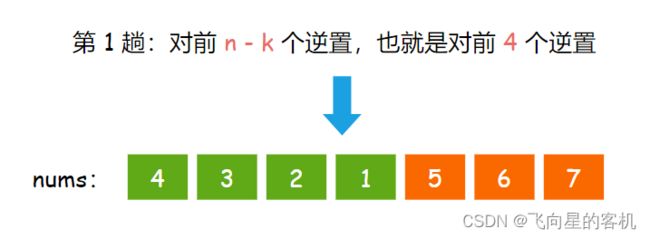
因为第 1 趟要对前 n - k 逆置，此时 n = 7，k = 3，那么就是要对前 4 个逆置，但是数组的下标是从 0 开始的，也就是说前 4 个元素的下标是 0 到 3，如图所示

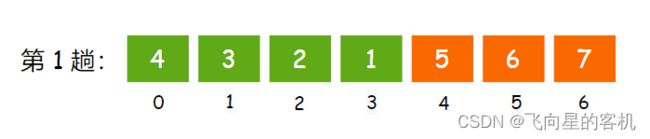
第 2 趟，对数组的后 k 个逆置，也就是后 3 个元素逆置，也就是从下标 4 到 6 开始逆置，如图所示

第 3 趟，把整个数组逆置，如图所示

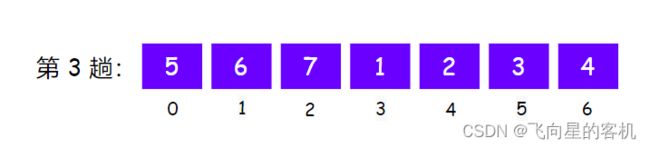
但是我们还要注意一个问题，如果 k 超过了数组元素的个数，怎么办呢？

比如：数组是 [ 1 2 3 4 5 ] ，k = 6 的时候，此时数组元素个数为 5，而要求向右旋转 6 个位置，如果按照上面分析的情况，第一趟对前 n - k 逆置，也就是 5 - 6 个逆置，难道对前 -1 个逆置吗？

我们先来看一下把数组向右轮转 6 个位置会怎么样，如图所示

咦！你会发现最后结果不就是 向右轮转 1 个位置 了吗？

此时我们要记住这道题的核心叫 轮转数组，也就是当轮转的次数超过数组长度的时候，又是新的一轮了！

所以我们可以先对 k 取余，然后再次旋转；比如数组长度为 8，我要向右轮转 10 次，其实就是向右轮转了 2 次，那么 10 % 2 的结果补就是 2 吗？

所以，如果 k 大于数组长度，故首先对 k 取余，然后再次旋转，这不会影响最终结果！

接口代码

void reverse(int* nums, int left, int right) {
	while (left < right) {
		int tmp = nums[left];
		nums[left] = nums[right];
		nums[right] = tmp;
		++left;
		--right;
	}
}

void rotate(int* nums, int numsSize, int k) {
    k %= numsSize; // 如果k大于数组长度，先对k取余
	reverse(nums, 0, numsSize - k - 1);
	reverse(nums, numsSize - k, numsSize - 1);
	reverse(nums, 0, numsSize - 1);
}

提交结果