生成对抗网络（GAN）及pytorch小例子

GAN是一种生成模型，包含两个部分，生成器G（Generator）和鉴别器D（Discriminator）。生成器用来产生虚假数据，鉴别器是用来判断该数据是否真实（输出是0到1之间的数字，值越大表示越接近真实数据）。生成器试图用虚假数据骗过鉴别器，而鉴别器又不断提高自己判别真假的能力。这是一个相互博弈的过程。经过多轮训练后，生成器产生的数据会越来越接近真实数据，这就是我们想要的结果了。
生成器和鉴别器都是神经网络。鉴别器用来判断输入数据是否为真，是一个二分类器，最后接sigmoid函数，输出0到1之间的值，用D(x)表示。假如标签用y表示（1表示为真，0表示为假）。则鉴别器的交叉熵损失函数为：
$$\underset{D}{\min }\{-y\log D(\mathbf{x})-(1-y)\log (1-D(\mathbf{x}))\}$$
对于生成器来说，首先我们要随机产生一些参数z输入到生成器得到G(z)。我们的目标是是鉴别器将其识别为真实数据，即D(G(z))≈1。换句话说，当y=0时，我们要最大化交叉熵损失函数：
$$\underset{G}{\max }\{-(1-y)\log (1-D(G(\mathbf{z})))\}=\underset{G}{\max }\{-\log (1-D(G(\mathbf{z})))\}.$$
如果鉴别器表现很好的话，D(G(z))≈0，那么损失函数相应也会很小，这样就不利于用梯度下降方法优化生成器。实际中，我们会最小化下面的交叉熵损失函数来代替：
$$\underset{G}{\min }\{-y\log (D(G(\mathbf{z})))\}=\underset{G}{\min }\{-\log (D(G(\mathbf{z})))\},$$
此时取y=1。

pytorch 实现

首先导入包。

%matplotlib inline
import matplotlib.pyplot as plt
from torch.utils.data import DataLoader
from torch import nn
import numpy as np
import torch

这里只是一个GAN的简单应用，我们就只生成一些少量数据。

X = np.random.normal(size=(1000, 2))
A = np.array([[1, 2], [-0.1, 0.5]])
b = np.array([1, 2])
data = X.dot(A)+b

plt.figure(figsize=(3.5,2.5))
plt.scatter(X[:100,0],X[:100,1],color='red')
plt.show()
plt.figure(figsize=(3.5,2.5))
plt.scatter(data[:100,0],data[:100,1],color='blue')
plt.show()

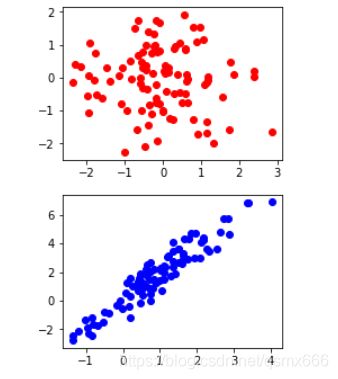
以上是我们随机生成的真实数据，GAN要做的就是生成尽可能和它相似的数据。

定义迭代器

batch_size = 8
data_iter = DataLoader(data, batch_size=batch_size)

生成器 Generator

class net_G(nn.Module):
    def __init__(self):
        super(net_G, self).__init__()
        self.model = nn.Sequential(
            nn.Linear(2, 2),
        )
        self._initialize_weights()

    def forward(self, x):
        x = self.model(x)
        return x

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                m.weight.data.normal_(0, 0.02)
                m.bias.data.zero_()

鉴别器 Discriminator

class net_D(nn.Module):
    def __init__(self):
        super(net_D, self).__init__()
        self.model = nn.Sequential(
            nn.Linear(2, 5),
            nn.Tanh(),
            nn.Linear(5, 3),
            nn.Tanh(),
            nn.Linear(3, 1),
            nn.Sigmoid()
        )
        self._initialize_weights()

    def forward(self, x):
        x = self.model(x)
        return x

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Linear):
                m.weight.data.normal_(0, 0.02)
                m.bias.data.zero_()

训练

首先定义一个函数来更新鉴别器的参数。

def update_D(X, Z, net_D, net_G, loss, trainer_D):
    batch_size = X.shape[0]
    ones = torch.ones(batch_size).view(batch_size, 1)
    zeros = torch.zeros(batch_size).view(batch_size, 1)
    real_Y = net_D(X)
    fake_X = net_G(Z)
    fake_Y = net_D(fake_X)
    loss_D = (loss(real_Y, ones)+loss(fake_Y, zeros))/2
    loss_D.backward()
    trainer_D.step()
    return loss_D.sum()

X是真实数据，传入到鉴别器中得到真实的标签real_Y。Z是随机产生的参数，输入到生成器中得到虚假的数据fake_X，再将fake_X传入到鉴别器中得到虚假的标签fake_Y，计算损失函数。

生成器也用类似的方法更新参数，需要注意损失函数是不一样的。

def update_G(Z, net_D, net_G, loss, trainer_G):
    batch_size = Z.shape[0]
    ones = torch.ones((batch_size,)).view(batch_size, 1)
    fake_X = net_G(Z)
    fake_Y = net_D(fake_X)
    loss_G = loss(fake_Y, ones)
    loss_G.backward()
    trainer_G.step()
    return loss_G.sum()

整个训练过程如下。每次迭代先更新鉴别器再更新生成器。

def train(net_D, net_G, data_iter, num_epochs, lr_D, lr_G, latent_dim, data):
    loss = nn.BCELoss()  # 二分类
    trainer_D = torch.optim.Adam(net_D.parameters(), lr=lr_D)
    trainer_G = torch.optim.Adam(net_G.parameters(), lr=lr_G)
    plt.figure(figsize=(7, 4))
    d_loss_point = []
    g_loss_point = []
    d_loss = 0
    g_loss = 0
    for epoch in range(1, num_epochs+1):
        d_loss_sum = 0
        g_loss_sum = 0
        batch = 0
        for X in data_iter:
            batch += 1
            X = torch.tensor(X, dtype=torch.float32)
            batch_size = X.shape[0]
            Z = torch.tensor(np.random.normal(
                0, 1, (batch_size, latent_dim)), dtype=torch.float32)
            trainer_D.zero_grad()
            d_loss = update_D(X, Z, net_D, net_G, loss, trainer_D)
            d_loss_sum += d_loss
            trainer_G.zero_grad()
            g_loss = update_G(Z, net_D, net_G, loss, trainer_G)
            g_loss_sum += g_loss
        d_loss_point.append(d_loss_sum/batch)
        g_loss_point.append(g_loss_sum/batch)

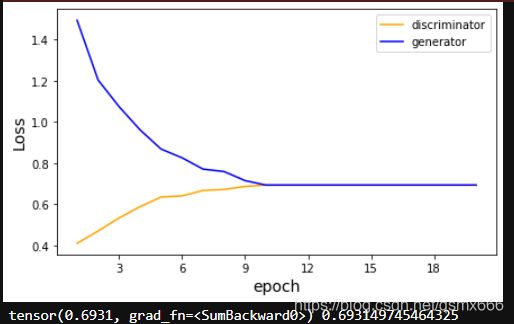
    plt.ylabel('Loss', fontdict={'size': 14})
    plt.xlabel('epoch', fontdict={'size': 14})
    plt.xticks(range(0, num_epochs+1, 3))
    plt.plot(range(1, num_epochs+1), d_loss_point,
             color='orange', label='discriminator')
    plt.plot(range(1, num_epochs+1), g_loss_point,
             color='blue', label='generator')
    plt.legend()
    plt.show()
    print(d_loss, g_loss)

    Z = torch.tensor(np.random.normal(
        0, 1, size=(100, latent_dim)), dtype=torch.float32)
    fake_X = net_G(Z).detach().numpy()
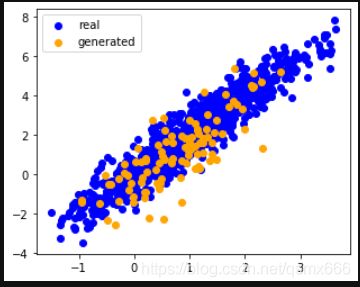
    plt.figure(figsize=(5, 4))
    plt.scatter(data[:, 0], data[:, 1], color='blue', label='real')
    plt.scatter(fake_X[:, 0], fake_X[:, 1], color='orange', label='generated')
    plt.legend()
    plt.show()

经过多次迭代优化后，生成器已经能产生接近真实值的数据。我们再随机初始化参数Z，传入到生成器中，就能得到结果。

if __name__ == '__main__':
    lr_D, lr_G, latent_dim, num_epochs = 0.05, 0.005, 2, 20
    generator = net_G()
    discriminator = net_D()
    train(discriminator, generator, data_iter, num_epochs, lr_D, lr_G, latent_dim, data)

结果如下：


黄色点即为生成的数据。