AcWing 889. 满足条件的01序列（卡特兰组合数，快速幂/扩欧/优化版预处理求逆元）

给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数都不少于 1 的个数的序列有多少个。

输出的答案对 10^9+7 取模。

输入格式
共一行，包含整数 n。

输出格式
共一行，包含一个整数，表示答案。

数据范围
1≤n≤10^5

输入样例：
3

输出样例：
5

转载了一位良心大大的文章，写的太好了，代码是自己写的两个改良版本（快速幂和扩欧），大大降低了时间复杂度。

转自AcWing 889. 满足条件的01序列。

题目描述

给定 n 个 0 和 n 个 1，它们将按照某种顺序排成长度为 2n 的序列，求它们能排列成的所有序列中，能够满足任意前缀序列中 0 的个数 都不少于（大于等于） 1 的个数 的序列有多少个。答案对 10^9+7 取模（显然是一个质数，从这里可以看出后续可用快速幂求逆元）。

1.案例

三个0，三个1

如果要求满足题目条件，则第一个数必须是0，最后一个数必须是1

0 0 0 1 1 1
0 0 1 1 0 1
0 0 1 0 1 1
0 1 0 0 1 1
0 1 0 1 0 1

2.题目分析

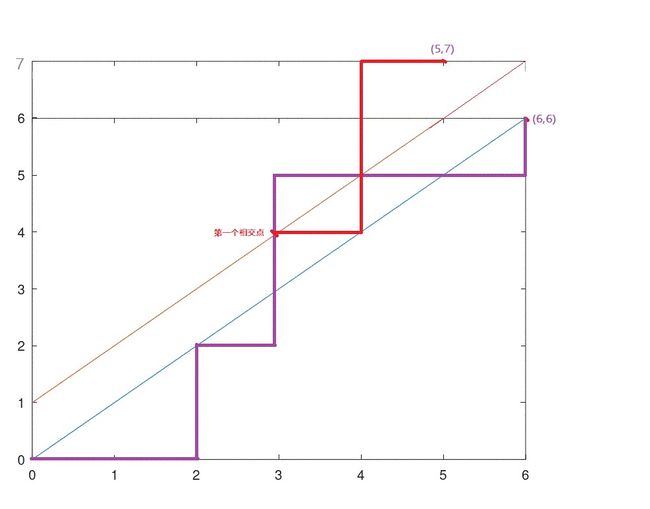
如果n等于6，即6个0和6个1

（1）可将题目转化为从原点（0，0）走到终点（6，6）有多少路径的问题

即把每一种数列转化成一种路径

0：向右走一格

1：向上走一格

也就是说 可以把任何一个排列转化成从（0，0）走到（6，6）的路径，

任何一条从（0，0）走到（6，6）的路径都可以转化成一个排列

需要满足：任意前缀序列的 0 的个数都不少于 1 的个数，则 x>=y

即满足条件的路径可以经过蓝边，但是绝对不能经过红边

3. 问题转化为

从（0，0）到（n，n）不经过红边的所有路径个数，即：总共的方案数 - 经过红边的方案数

总方案数：

原因：从（0，0）到（6，6）一共需要12步，挑选6步向上走。所以总方案数为：

经过红颜色边的路径个数：

案例: 0 0 1 1 0 1 1 1 0 0 0 1

我们惊奇的发现：

对于任何一条经过红颜色边的路径，找到第一个走到红颜色边的点（第一个与红颜色边相交的点），将这条路径从这个点的后半部分关于红颜色边做轴对称，（6，6）的对称点为（5，7）。

即任何经过红颜色边的点都可以使用这种方式，找到第一个走到红颜色边的点，将后面的部分关于红颜色边做轴对称，则终点一定是（5，7）（即（6，6）关于红颜色边的对称点）。

任何一条从（0，0）到（6，6）经过红颜色边的点，通过上述方式都可以变成一条从（0，0）走到（5，7）的路径；而任意一条从（0，0）走到（5，7）的路径都会经过红颜色边，找到第一个经过红颜色边的点，关于红颜色边做轴对称，可以变成一条从（0，0）走到（6，6）并经过红颜色边的路径。

即从（0，0）走到（5，7）的路径与从（0，0）走到（6，6）且经过红颜色边的路径一一对应。

从（0，0）到（5，7）的所有路径为 ，

则从（0，0）到（6，6）经过红颜色边的路径也为，

从（0，0）到（6，6）不经过红边的所有路径个数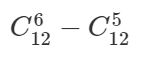：（题解） ，
进行一般化，从（0，0）到（n，n）不经过红边的所有路径个数： （一般化）。

4. 公式化简

即 (卡特兰数)

写法一：快速幂求逆元（20 ms）

详情请戳这：快速幂求逆元

#include

using namespace std;

#define int long long
const int mod = 1e9 + 7;
int n;

int qmi(int a,int b)
{
    int res = 1;
    while(b)
    {
        if (b&1) res = res * a % mod;
        b>>=1;
        a = a * a % mod;
    }
    return res;
}

signed main()
{
    cin>>n;
    // 套卡特兰数计算公式就行
    int up = 1, down = 1;
    for(int i=2*n,j=1;j<=n;--i,++j)
    {
        up = up * i % mod;//分子
        down = down * j % mod;//分母
    }
    int res = 1;
    res = res * up * qmi(down,mod-2) % mod;//先乘上分子和分母的模mod逆元
    res = res * qmi(n+1, mod-2) % mod;//最后根据公式乘上n+1的模mod逆元

    cout<

写法二：扩展欧几里得求逆元（19 ms）

详情请戳这：扩欧求逆元

#include

using namespace std;

#define int long long
const int  mod = 1e9 + 7;
int n;

void exgcd(int a, int b, int &d, int &x, int &y)
{
    if (!b)
    {
        d = a, x = 1, y = 0;
        return ;
    }
    exgcd(b, a % b, d, y, x), y-=a/b*x;
}

signed main()
{
    cin>>n;
    //分别求分子分母
    int up = 1, down = 1;
    for(int i=2*n,j=1;j<=n;--i,++j)
    {
        up = up * i % mod;
        down = down * j % mod;
    }
    //接下来都是套公式了
    int res, x, y, d;
    res = 1;
    res = res * up % mod;//先乘上分子
    exgcd(down,mod,d,x,y);//扩欧求分母的模mod逆元
    res = res * x % mod;//后乘上分母的模mod逆元

    exgcd(n+1, mod, d, x, y);//扩欧求n+1的模mod逆元
    res = (res * x % mod + mod) % mod;//最后根据公式乘上n+1的模mod逆元，注意这样写是为了防止出现负数！
    cout<

写法三：经过优化后的预处理写法：（59 ms）

详情请戳这：预处理优化的O(n)版本

倒序求阶乘的逆元，每次循环都在原版预处理做法基础上节省了一个快速幂求逆元的时间（每次快速幂求逆元需要log mod）

#pragma GCC optimize(2)
#include

using namespace std;
#define int long long
const int mod = 1e9+7;

inline int qmi(int a,int b)
{
    int res = 1;
    while(b)
    {
        if(b&1) res = res * a % mod;
        b>>=1;
        a = a * a % mod;
    }
    return res;
}

const int N = 2e5+10;
int fac[N],infac[N];

inline void init()
{
    fac[0] = infac[0] = 1;
    for (int i = 1; i < N; i++) fac[i] = fac[i - 1] * i % mod;

    infac[N - 1] = qmi(fac[N - 1], mod - 2);

    for (int i = N - 2; i >= 1; i--) infac[i] = infac[i + 1] * (i + 1) % mod;//将推出来的递推公式变一下形
}

signed main()
{
    init();
    int n;
    cin>>n;
    //c{2*n,n}-c{2*n,n-1}
    int a = fac[2*n]*infac[n]%mod*infac[n]%mod;
    int b = fac[2*n]*infac[n-1]%mod*infac[n+1]%mod;
    cout<<((a-b)+mod)%mod<