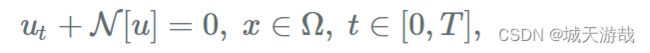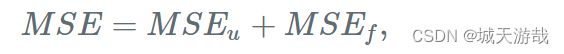（PINNs）物理信息神经网络的浅理解

Physics Informed Deep Learning

（一）前言

        物理信息神经网络的作者有Maziar Raissi, Paris Perdikaris, and George Em Karniadakis，此网络主要用于偏微分方程的解，根据可用数据的性质和排列，设计了两类不同的算法，即连续时间和离散时间模型。其中设计一些方程，如 Burgers’ Equation、Shrödinger Equation、Allen-Cahn Equation 等。在github官网有全部代码。本文主要是对PINNs代码的调通与浅理解。

（二）代码调通

        由随着计算机快速发展，许多编程语言、编辑器、框架等等都在飞快更新版本，github上拉取的PINNs的代码需要2019年及更早前的版本。本文主要采用的架构为：python 3.7.0 + tensorflow 1.15.4   其它包手动点击下载即可。

        其中遇到的一些问题：

1.plotting包下载不了

        点击 Install package plotting 下载了许多次都没反应，最后发现这个plotting是自己写的python模块，不管的话其实运行也不会报错，只是编译显示出错，这是动态加入路径调整的问题。即：

         如果想要不报错的话可以在 File->Settings->Project:你的项目名->Project Structure中将 PINNs-master 加入源路径。 然后点击应用，即可解决编译报错。

2.tensorflow 2.0及以上版本不兼容

        即使使用 import tensorflow.compat.v1 as tf 也还有一个错 即 tf.contrib，因为高版本所有的都弃用了 contrib，故而只能将 tensorflow版本降低了。重新使用 conda 创建虚拟环境，安装 python 3.7 与 tensorflow 1.15.4 的时候就可以运行了。

3. savefig 不能画图问题

         代码最后一行 savefig() 注释了，因为 figures 文件中有一份保存的图，如果想要重新画图，可以去掉注释 #，但电脑会报错，需要安装 texlive，需要去网上下载安装包，而不是在 conda 里面直接下载。我是下载的压缩文件，解压缩后为

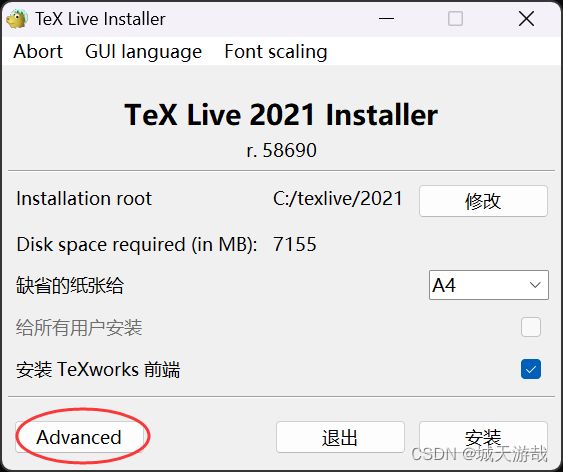
        打开texlive，然后双击打开 install-tl-windows 文件

         点击 Advanced，根据需要选择一些信息，然后点击安装，大概需要等待半个小时左右

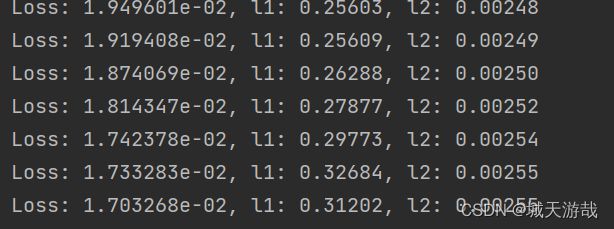
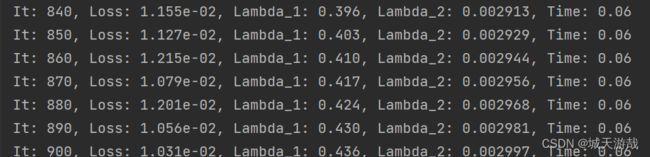
         这样差不多就可以运行代码了。运行过程如下图所示

（三）代码分析

 1.神经网络层数 layers 与 函数 u(t,x)

         其神经网络共有 9 层，每层输入输出（input，output）形状大小（shape）按顺序第一层为（2，20），第二层到第八层都是（20，20），最后一层为（20，1）。浅理解就是输入两种数据，即 x 与 t，输出一种数据，即 u。在方程中 u 是关于 x 与 t 的函数，即 u(t,x)，

 2.训练 model

         X_u_train 的 shape 为（2000，2），其中两列数据分别为 x 与 t 。u_train 的 shape 为（2000，1），一列数据为 u 。layers 同上 。lb 为两列中两个最小值[-1，0] 。ub为两列中两个最大值[1，0.99]。

3.f(t,x)函数 

        官网 Burgers’ Equation 中函数f(t，x)被定义为  

 

         其中 u_t 为函数 u(t,x) 对 t 求梯度，u_x 为函数 u(t,x) 对 x 求梯度，u_xx 为函数 u(t,x) 对 x 求两次梯度。

         由于上式令为 f，即 函数 f(t,x) 的值一般为 0 ，在深度学习中有损失值，其 pre 值一般在 0 附近。

4.均方差 MSE

        此物理信息神经网络与一般的神经网络不用，其损失使用的 MSE 由两部分组成，即：

 

         一个是对函数 u(t,x) 求均方差，一个是对函数 f(t,x) 求均方差，再由两者相加而成。其为PINN与一般的神经网络最大的区别，引入物理特性加入损失函数。

5.PINN的浅谈

        PINN在求偏微分方程中有不错的效果，能够利用较少的训练集得到较高的精确度，而这也正是它的缺点，数据较大时，训练速度非常慢，增加一个维度的数据，其运行速度几乎呈指数增长。