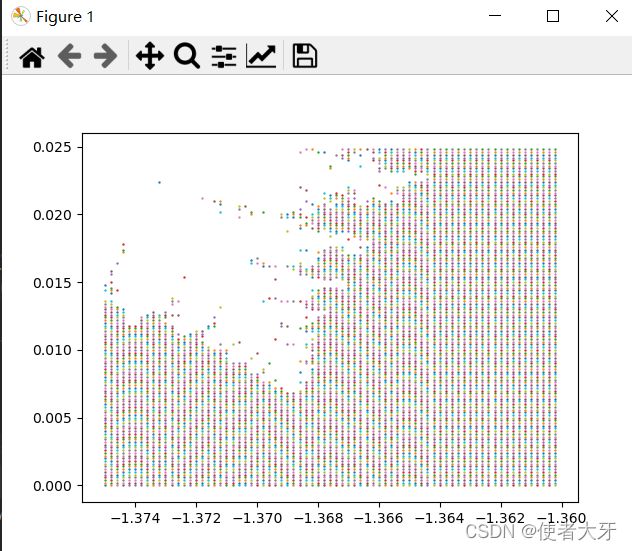
基于Python画曼德勃罗集
最近有点迷分型几何，看到“上帝指纹”曼德勃罗集，想用Python实现一下。
源码很简单20行不到。
import matplotlib.pyplot as plt
import numpy
def mb(x,y):
C = complex(x,y)
Z = 0
for i in range(100):
Z = Z*Z +C
if abs(Z)>2:
return False
return True
for x in numpy.arange(-2,2,0.01):
for y in numpy.arange(-1,1,0.01):
if mb(x,y):
plt.scatter(x,y,s=0.5)
plt.show()
运行结果↓
由于电脑性能受限，步长实在是不能取的太精细。。。实在有点丑。附上网图一张。
从运行结果来看（也是一步一步探索出来的），曼德勃罗集的C的范围大概是：实部∈(-2,0.5)，虚部∈(-1,1)。（这里不禁吐槽下，关于曼德罗集的图片很多，但是几乎没有人标上坐标轴）。
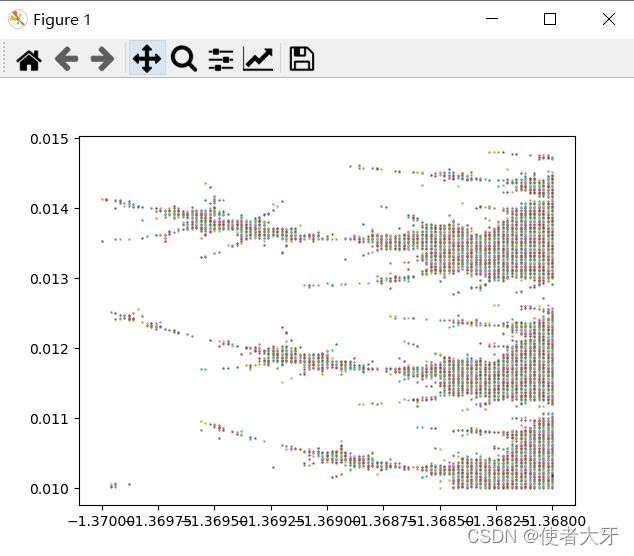
既然有了代码，我们就可以再看下细节。
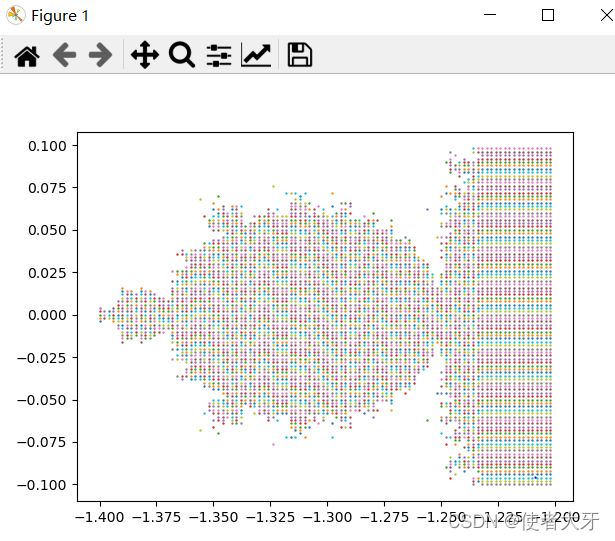
继续放大（当然毫无疑问，肯定是无限细节）
最后再放大一下
------------------更新-----------------
发现用imshow的方式画出的图会好看很多，直接再附源码
from PIL import Image
import numpy as np
import matplotlib.pyplot as plt
import math
def mb(x, y):
C = complex((x - 1500) /600, (500 - y) / 500)
Z = 0
for i in range(200):
Z = Z**2 + C
if abs(Z)>2:
return False
return True
image = Image.new('RGB', (2000, 1000))
image_array = np.array(image)
for k in range(1000):
for v in range(2000):
if mb(v, k):
image_array[k, v, :] = 255
else:
image_array[k, v, 0] = abs((v - 1500) /600 * 255/(1500/600))
image_array[k, v, 1] = abs((500 - k) / 500 * 255)
image_array[k, v, 2] = abs((v - 1500) /600 * 255/(1500/600)/2 + (500 - k) / 500 * 255/2)
plt.imshow(image_array)
plt.show()
运行如下↓
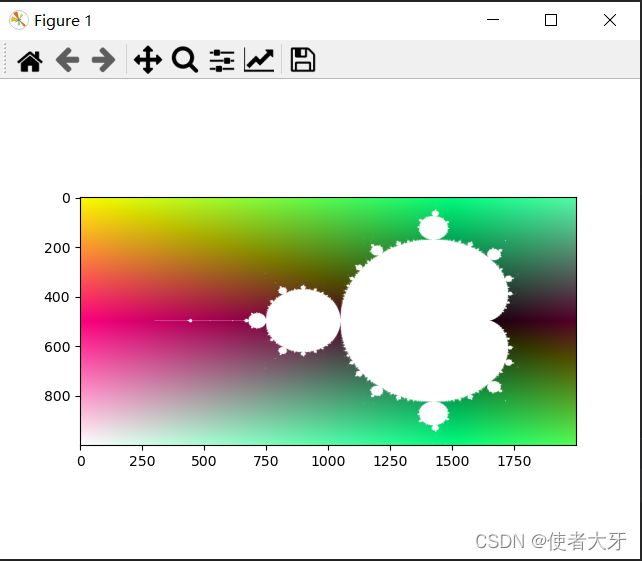
既然有了美美的代码，就可以玩点花的了：稍微改下曼德勃罗集的公式。
Zn+1 = Zn^3 + C 结果↓
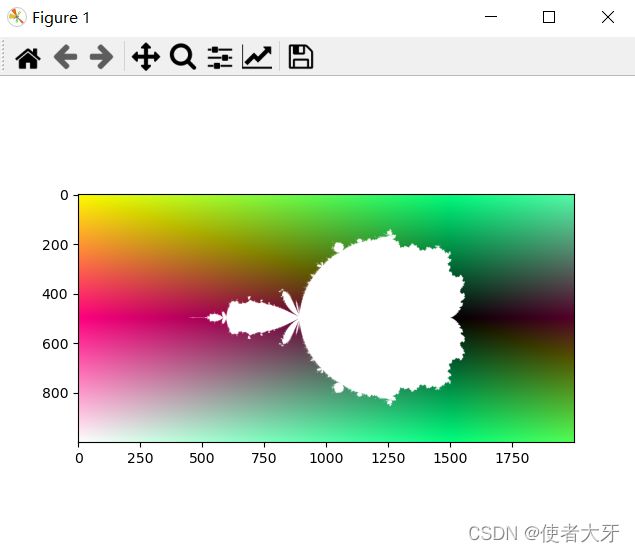
Zn+1 = Zn^2+Zn + C 结果↓（这个挺好看的）
-----------------再更新-------------------
（没想到这个还能再更一次。。。）
根据迭代公式，实现了曼德勃罗集的绘制。
那么如果不仅限于二维，如果扩展到三维会是怎么样的？
很遗憾，曼德勃罗集在三维上是不存在的。但是可以在四维上用双复数，按照曼德勃罗集的迭代方式构建四维的曼德勃罗集：曼德尔球
思维再扩展一下，那么能否也用简单的迭代规则，构建一个三维的分型呢？
我自己构建了一个规则，但是受制于电脑性能，并未看出它的分型结构（而且从初步的结果来看，它很有可能还不是分型的，看起来似乎是有解析解）
构建这个三维图形的规则如下：
这里我们要找的集合就是这样的 Z1 的集合，使得在有限次迭代后，Zn能够收敛
说明：
- 这里向量的每次迭代都是用外积，理由也很简单，两个向量外积之后仍然是向量，能够迭代下去；
- 这里指定了Z0 是单位向量（1，1，1），实际上Z0也可以取任意值，然后找出Z0的集合（这个集合也就和Z1一样），这里为了减少计算机的工作量，指定了Z0为单位向量。
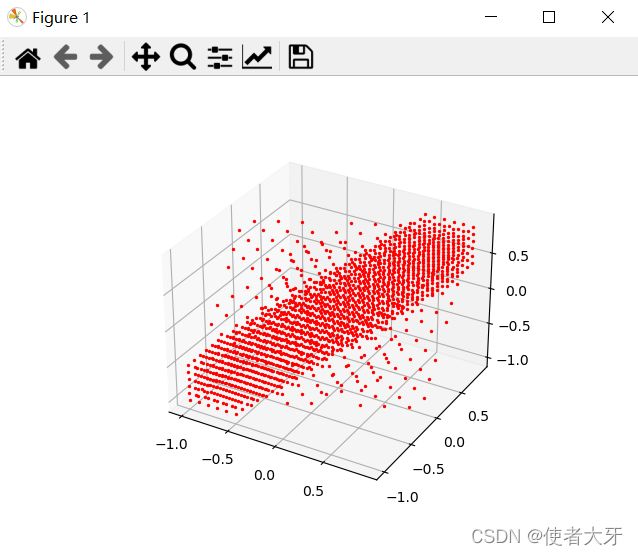
运行结果
受制于电脑的性能，点云没办法取得太密集。
从下面Z1的集合来看，并不能看出分型的结构。
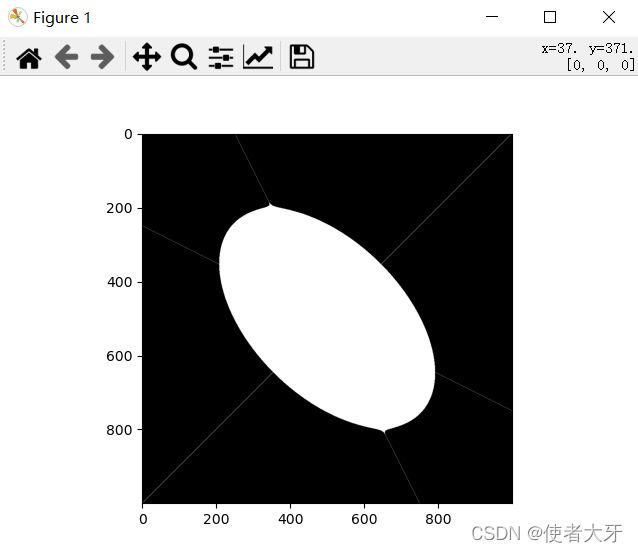
既然三维结构看不出来的话，只能取截面看看它的形状。
奇怪且有趣的是，这个集合似乎在xoy, yoz, zox三个面上的截面图形都是一样的。
最后，如果有代码大神能绘制出这个集合的三维图像，还请指教一下。
最后的最后，附上源码
import matplotlib.pyplot as plt
from PIL import Image
import numpy
import warnings
warnings.filterwarnings("ignore")
def iter(x,y,z):
x1, y1, z1=1, 1, 1
x2 = z-y
y2 = x-z
z2 = y-x
for i in range(10):
x_mid = y1*z2 - y2*z1
y_mid = z1*x2 - z2*x1
z_mid = x1*y2 - x2*y1
x1 = x2
y1 = y2
z1 = z2
x2 = x_mid
y2 = y_mid
z2 = z_mid
# print(x2,y2,z2)
if abs(x2) and abs(y2) and abs(z2) >1:
return False
else:
return True
#-------------------------三维点云---------------------------------
# fig = plt.figure()
# ax = fig.add_subplot(111, projection='3d')
#
# k =10
# for x in range(-k,k):
# for y in range(-k,k):
# for z in range(-k, k):
# if iter(x/k, y/k, z/k):
# ax.scatter(x/k, y/k, z/k,s=2, c='r')
#
# plt.show()
#----------------------------------------------------------------
#----------------xoy二维截面------------------------------------------
# image = Image.new('RGB', (1000, 1000))
# image_array = numpy.array(image)
#
# k=500
# for x in range(-k,k):
# for y in range(-k,k):
# if iter(x/k, y/k, 0):
# image_array[x+k,y+k]= 255
# else:
# image_array[x+k, y+k] = 0
#
# plt.imshow(image_array)
# plt.show()
#----------------------------------------------------------------
#----------------xoz二维截面------------------------------------------
# image = Image.new('RGB', (1000, 1000))
# image_array = numpy.array(image)
#
# k=500
# for x in range(-k,k):
# for z in range(-k,k):
# if iter(x/k, 0, z/k):
# image_array[x+k,z+k]= 255
# else:
# image_array[x+k, z+k] = 0
#
# plt.imshow(image_array)
# plt.show()
#----------------------------------------------------------------
#----------------yoz二维截面------------------------------------------
image = Image.new('RGB', (1000, 1000))
image_array = numpy.array(image)
k=500
for y in range(-k,k):
for z in range(-k,k):
if iter(0, y/k, z/k):
image_array[y+k,z+k]= 255
else:
image_array[y+k, z+k] = 0
plt.imshow(image_array)
plt.show()
#----------------------------------------------------------------