Python数据分析-数据预处理
数据预处理
文章目录
- 数据预处理
-
- 1.前言
- 2.数据探索
-
- 2.1缺失值分析
- 2.2 异常值分析
-
- 2.2.1 简单统计量分析
- 2.2.2 3$\sigma$原则
- 2.2.3 箱线图分析
- 2.3 一致性分析
- 2.4 相关性分析
- 3.数据预处理
-
- 3.1 数据清洗
-
- 3.1.1 缺失值处理
- 3.1.2 异常值处理
- 3.2 数据集成
-
- 3.2.1 实体识别
- 3.2.2 冗余属性识别
- 3.2.3 数据变换
- 3.2.4 规范化
- 3.2.5 连续属性离散化
- 3.2.6属性构造
- 3.3 数据归约
-
- 3.3.1 属性归约
- 3.3.2 数值归约
- 3.3.2 数值归约
1.前言
数据质量分析是数据预处理的前提,是数据挖掘分析结论有效性和准确性的基础,其主要任务是检查原始数据中是否存在脏数据,脏数据一般指的是不符合要求的,以及不能直接进行相应分析的数据。
脏数据包括:
-
缺失值
-
异常值
-
不一致的值
-
重复数据及含有特殊符号(如#、¥、*)的数据
2.数据探索
2.1缺失值分析
data.describe()#查看数据的基本情况
len(data)#查看数据的总条数
2.2 异常值分析
检查数据中是否有录入错误以及含有不合理的数据,忽视这些异常值是十分危险的,可能会导致数据整体分析产生明显偏离观察值的影响。
2.2.1 简单统计量分析
通过一个简单的描述性估计,进而查看哪些数据是不合理的。需要的统计量可以是最大值和最小值,判断这个变量的极值是否不在现实合理范围之中。
data = pd.read_excel(catering_sale, index_col = '日期') # 读取数据,指定“日期”列为索引列
data.describe()#对数据进行描述性估计,显示如下数据
#输出:
销量
count 200.000000
mean 2755.214700
std 751.029772
min 22.000000
25% 2451.975000
50% 2655.850000
75% 3026.125000
max 9106.440000
2.2.2 3 σ \sigma σ原则
l如果数据服从正态分布,在 3 σ 3\sigma 3σ原则下,异常值被定义为一组测定值中与平均值的偏差超过三倍标准差的值。在正态分布的假设下,距离平均值 3 σ 3\sigma 3σ之外的值出现的概率小于0.003,属于极个别的小概率事件。
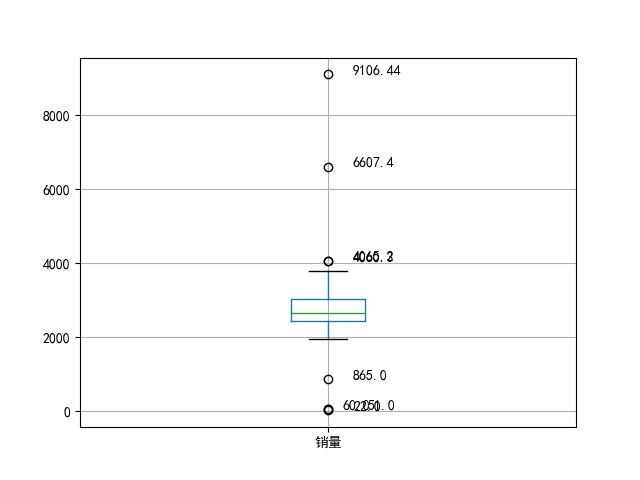
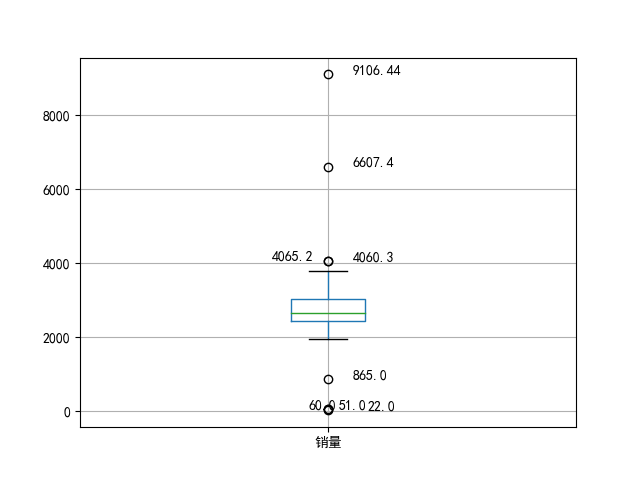
2.2.3 箱线图分析
箱形图判断异常值的标准以四分位数和四分位距为基础,四分位数具有一定的鲁棒性:多达25%的数据可以变得任意远而不会很大地扰动四分位数,其结果比较客观,在识别异常值时有一定优越性
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签--黑体
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.figure() # 建立图像
p = data.boxplot(return_type='dict') # 画箱线图,直接使用DataFrame的方法
#获取异常值,'flies'为箱线图中异常值的标签
x = p['fliers'][0].get_xdata()
y = p['fliers'][0].get_ydata()
y.sort() # 从小到大排序,该方法直接改变原对象
for i in range(len(x)):
if i>0:
plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.05 -0.8/(y[i]-y[i-1]),y[i]))
else:
plt.annotate(y[i], xy = (x[i],y[i]), xytext=(x[i]+0.08,y[i]))
plt.show() # 展示箱线图
将y数据进行排序后的图:
2.3 一致性分析
数据不一致性是指数据的矛盾性、不相容性。直接对不一致的数据进行挖掘,可能会产生与实际相违背的挖掘结果。
在数据挖掘过程中,不一致数据的产生主要发生在数据集成的过程中,可能是由于被挖掘数据是来自于从不同的数据源、重复存放的数据未能进行一致性地更新造成的,比如两张表中都存储了用户的地址,在用户的地址发生改变时,如果只更新了一张表中的数据,那么这两张表中就有了不一致的数据。
2.4 相关性分析
-
绘制散点图
-
绘制散点图矩阵
-
计算相关系数
- Pearson相关系数
import pandas as pd D = pd.DataFrame([range(1, 8), range(2, 9)]) # 生成样本D,一行为1~7,一行为2~8 print(D.corr(method='spearman')) # 计算相关系数矩阵 S1 = D.loc[0] # 提取第一行 S2 = D.loc[1] # 提取第二行 print(S1.corr(S2, method='pearson')) # 计算S1、S2的相关系数- 协方差系数
import numpy as np D = pd.DataFrame(np.random.randn(6, 5)) # 产生6×5随机矩阵 print(D.cov()) # 计算协方差矩阵 print(D[0].cov(D[1])) # 计算第一列和第二列的协方差
3.数据预处理
3.1 数据清洗
3.1.1 缺失值处理
| 插补方法 | 描述 |
|---|---|
| 均值/中位数/众数插补 | 根据属性的类型,用该属性的这些特征进行插补 |
| 使用固定值 | 用一个常量替换 |
| 最近邻插补法 | 记录中找到与缺失样本最接近的该属性值插补 |
| 回归方法 | 根据已有数据与相关量建立拟合模型来预测属性值 |
| 插值法 | 利用已知点建立合适的插值函数,未知点由插值函数近似代替 |
import pandas as pd # 导入数据分析库Pandas
from scipy.interpolate import lagrange # 导入拉格朗日插值函数
inputfile = '../data/catering_sale.xls' # 销量数据路径
outputfile = '../tmp/sales.xls' # 输出数据路径
data = pd.read_excel(inputfile) # 读入数据
data['销量'][(data['销量'] < 400) | (data['销量'] > 5000)] = None # 过滤异常值,将其变为空值
# 自定义列向量插值函数
# s为列向量,n为被插值的位置,k为取前后的数据个数,默认为5
def ployinterp_column(s, n, k=5):
y = s[list(range(n-k, n)) + list(range(n+1, n+1+k))] # 取数
y = y[y.notnull()] # 剔除空值
return lagrange(y.index, list(y))(n) # 插值并返回插值结果
# 逐个元素判断是否需要插值
for i in data.columns:
for j in range(len(data)):
if (data[i].isnull())[j]: # 如果为空即插值。
data[i][j] = ployinterp_column(data[i], j)
data.to_excel(outputfile) # 输出结果,写入文件
3.1.2 异常值处理
| 异常值处理方法 | 方法描述 |
|---|---|
| 删除含有异常值的记录 | 直接将异常值删除 |
| 视为缺失值 | 将异常值视为缺失值,利用缺失值处理方法进行处理 |
| 平均值修正 | 可以用前后两个观测值的平均值修正该异常值 |
| 不处理 | 直接在异常值数据集上进行挖掘建模 |
3.2 数据集成
3.2.1 实体识别
实体识别是统一不同源数据的矛盾之处:
- 同名异义
- 异名同义
- 单位不统一
3.2.2 冗余属性识别
常见类型:
- 同一属性出现多次
- 同一属性命名不一致导致重复
可以通过相关分析检测,根据两个数值型属性,根据其属性值,用相关系数度量一个属性在多大程度蕴含另一个属性。
3.2.3 数据变换
对数据转换为“适当”形式,比如常见的函数变换,将数据进行简单压缩,将非平稳序列转换为平稳序列等等
3.2.4 规范化
-
最小-最大规范化
又称为离散标准化,对原始数据进行线性变换,将数值映射到[0,1]之间。
(data - data.min()) / (data.max() - data.min()) # 最小-最大规范化 -
零-均值规范化
标准差标准化,经过处理后的数据均值为0,标准差为1
(data - data.mean()) / data.std() # 零-均值规范化 -
小数定标准化
通过移动属性值的小数位数,将属性值映射到[-1,1]之间,移动的小数位数取决于属性值绝对值的最大值。
data / 10 ** np.ceil(np.log10(data.abs().max())) # 小数定标规范化
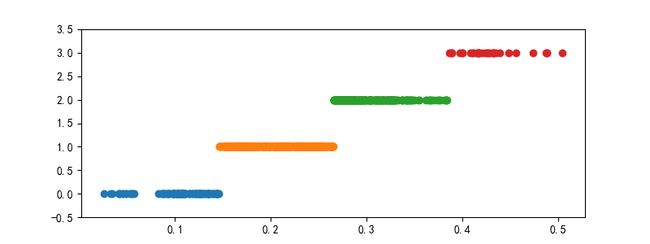
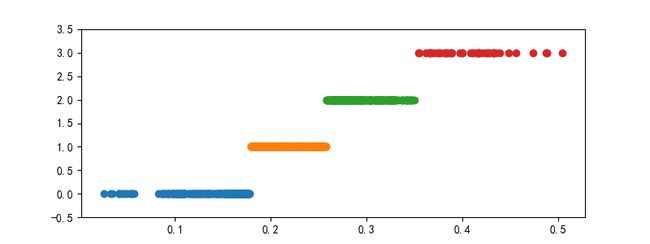
3.2.5 连续属性离散化
一些数据挖掘算法,特别是某些分类算法,如ID3,Apriori算法,要求数据是分类属性形式。
离散化过程:在数据的取值范围设定若干个离散的划分点,将取值范围划分为一些离散化的区间,最后用不同的符号或数值代表每个区间中的数值。也即是离散化涉及两个步骤:1.确定分类数,2.如何将连续属性映射到这些分类值
常用离散化方法:
-
等宽法
将属性的值域划分为具有相同宽度的区间,区间个数由数据本身特定决定或者用户指定
k=4#k为划分区间数 d1 = pd.cut(data, k, labels = range(k)) # 等宽离散化,各个类比依次命名为0,1,2,3 -
等频法
将相同数量的记录放进每个区间
w = [1.0*i/k for i in range(k+1)] w = data.describe(percentiles = w)[4:4+k+1] # 使用describe函数自动计算分位数 w[0] = w[0]*(1-1e-10) d2 = pd.cut(data, w, labels = range(k)) -
基于聚类分析的方法
- 首先将连续属性的值使用聚类算法(K-Means算法)进行聚类
- 然后再将聚类得到的簇进行处理,合并到一个簇的连续属性值做同一标记
3.2.6属性构造
为了帮助用户获得更好的数据,需要利用抑制属性构造新的属性,并加入到现有的属性集中。
3.3 数据归约
数据规约是将海量数据进行规约,规约之后的数据仍接近于保持原数据的完整性,但数据量小得多。
3.3.1 属性归约
属性规约常用方法有:合并属性、逐步向前选择、逐步向后删除、决策树归纳、主成分分析
| 属性归约 | 方法描述 |
|---|---|
| 合并属性 | 将一些旧属性合并为新属性 |
| 逐步向前选择 | 从一个空属性集开始,每次从原来属性选择一个当前最优的属性添加到属性子集中直到无法选出最优属性或满足一定阈值为止 |
| 逐步向后选择 | 类比于逐步向前选择,每次去除最差的属性 |
| 决策树归纳 | 利用决策树算法对初始数据进行分类归纳学习,生成一个初始决策树,没有出现的属性均视为无关属性 |
| PCA | 将许多相关性很高的变量转化为彼此相互独立或不相关变量 |
D = np.random.rand(10,4)
pca = PCA()#n_components默认为4,代表选取几个特征向量
pca.fit(D)
pca.components_ # 返回模型的各个特征向量
3.3.2 数值归约
- 直方图
- 聚类
- 抽样
学习书籍:
《Python数据分析与挖掘实战》张良均等著
分类归纳学习,生成一个初始决策树,没有出现的属性均视为无关属性 |
| PCA | 将许多相关性很高的变量转化为彼此相互独立或不相关变量 |
D = np.random.rand(10,4)
pca = PCA()#n_components默认为4,代表选取几个特征向量
pca.fit(D)
pca.components_ # 返回模型的各个特征向量
3.3.2 数值归约
- 直方图
- 聚类
- 抽样
学习书籍:
《Python数据分析与挖掘实战》张良均等著