【进阶一】Python实现MDCVRP常见求解算法——模拟退火（SA）

基于python语言，实现模拟退火算法（SA）对多车场车辆路径规划问题（MDCVRP）进行求解。

往期优质资源

• python实现6种智能算法求解CVRP问题
• python实现7种智能算法求解MDVRP问题
• python实现7种智能算法求解MDVRPTW问题
• Python版MDHFVRPTW问题智能求解算法代码【TS算法】
• Python版MDHFVRPTW问题智能求解算法代码【SA算法】
• Python版MDHFVRPTW问题智能求解算法代码【GA算法】
• Python版MDHFVRPTW问题智能求解算法代码【DPSO算法】
• Python版MDHFVRPTW问题智能求解算法代码【DE算法】
• Python版MDHFVRPTW问题智能求解算法代码【ACO算法】
• Python版HVRP问题智能求解算法代码【GA算法】
• Python版HVRP问题智能求解算法代码【DPSO算法】

1. 适用场景

• 求解MDCVRP 问题
• 车辆类型单一
• 车辆容量不小于需求节点最大需求
• 多车辆基地
• 各车场车辆总数满足实际需求

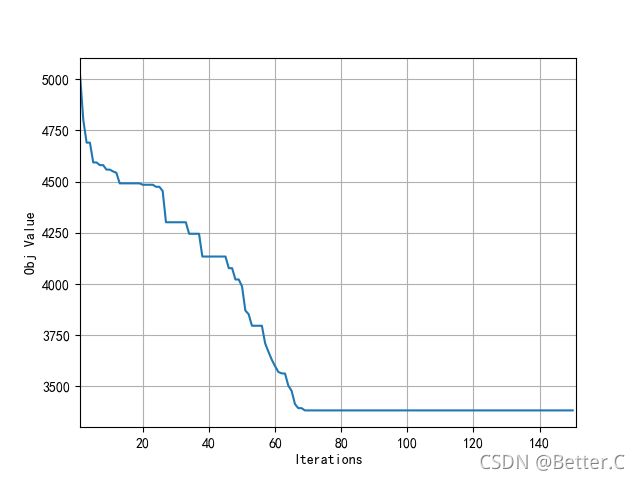
2. 求解效果

（1）收敛曲线

（2）车辆路径

3. 代码分析

车俩路径规划问题按照车场数量可分为单一车场路径规划问题和多车场路径规划问题。针对单一车场条件下仅考虑车辆容量限制的路径规划问题前边帖子中已实现SA算法求解，本文采用SA算法对多车场条件下仅考虑车辆容量限制的路径规划问题进行求解。为了保持代码的延续性以及求解思路的一致性，这里对上述SA算法代码进行如下主要修正实现MDCVRP问题的求解。

• Model数据结构类中采用demand_dict属性存储需求节点集合，depot_dict属性储存车场节点集合，demand_id_list属性储存需求节点id集合，distance_matrix属性储存任意节点间的欧式距离；
• Node数据结构类中去掉node_seq属性，增加depot_capacity属性记录车场的车队限制
• splitRoutes函数中分割车辆路径时分配最近车场作为其车辆提供基地（满足车场车队数量限制）

4. 数据格式

以csv文件储存数据，其中demand.csv文件记录需求节点数据，共包含需求节点id，需求节点横坐标，需求节点纵坐标，需求量；depot.csv文件记录车场节点数据，共包含车场id，车场横坐标，车场纵坐标，车队数量。需要注意的是：需求节点id应为整数，车场节点id任意，但不可与需求节点id重复。 可参考github主页相关文件。

5. 分步实现

（1）数据结构
为便于数据处理，定义Sol()类，Node()类，Model()类，其属性如下表：

• Sol()类，表示一个可行解

属性	描述
node_id_list	需求节点id有序排列集合，对应TSP的解
obj	优化目标值
routes	车辆路径集合，对应MDCVRP的解

• Node()类，表示一个网络节点

属性	描述
id	物理节点id
x_coord	物理节点x坐标
y_coord	物理节点y坐标
demand	物理节点需求
depot_capacity	车辆基地车队规模

• Model()类，存储算法参数

属性	描述
best_sol	全局最优解，值类型为Sol()
demand_dict	需求节点集合（字典），值类型为Node()
depot_dict	车场节点集合（字典），值类型为Node()
demand_id_list	需求节点id集合
distance_matrix	节点距离矩阵
opt_type	优化目标类型，0：最小车辆数，1：最小行驶距离
vehicle_cap	车辆容量

（2）文件读取

def readCsvFile(demand_file, depot_file, model):
    with open(demand_file,'r') as f:
        demand_reader=csv.DictReader(f)
        for row in demand_reader:
            node = Node()
            node.id = int(row['id'])
            node.x_coord = float(row['x_coord'])
            node.y_coord = float(row['y_coord'])
            node.demand = float(row['demand'])
            model.demand_dict[node.id] = node
            model.demand_id_list.append(node.id)

    with open(depot_file,'r') as f:
        depot_reader=csv.DictReader(f)
        for row in depot_reader:
            node = Node()
            node.id = row['id']
            node.x_coord=float(row['x_coord'])
            node.y_coord=float(row['y_coord'])
            node.depot_capacity=float(row['capacity'])
            model.depot_dict[node.id] = node

（3）计算距离矩阵

def calDistance(model):
    for i in range(len(model.demand_id_list)):
        from_node_id = model.demand_id_list[i]
        for j in range(i+1,len(model.demand_id_list)):
            to_node_id=model.demand_id_list[j]
            dist=math.sqrt( (model.demand_dict[from_node_id].x_coord-model.demand_dict[to_node_id].x_coord)**2
                            +(model.demand_dict[from_node_id].y_coord-model.demand_dict[to_node_id].y_coord)**2)
            model.distance_matrix[from_node_id,to_node_id]=dist
            model.distance_matrix[to_node_id,from_node_id]=dist
        for _,depot in model.depot_dict.items():
            dist = math.sqrt((model.demand_dict[from_node_id].x_coord - depot.x_coord) ** 2
                             + (model.demand_dict[from_node_id].y_coord -depot.y_coord)**2)
            model.distance_matrix[from_node_id, depot.id] = dist
            model.distance_matrix[depot.id, from_node_id] = dist

（4）初始解生成

def genInitialSol(node_id_list):
    node_id_list=copy.deepcopy(node_id_list)
    random.seed(0)
    random.shuffle(node_id_list)
    return node_id_list

（5）目标函数计算
适应度计算依赖" splitRoutes “函数对TSP可行解分割得到车辆行驶路线和所需车辆数，在得到各车辆行驶路线后调用” selectDepot “函数，在满足车场车队规模条件下分配最近车场，” calDistance "函数计算行驶距离。

def selectDepot(route,depot_dict,model):
    min_in_out_distance=float('inf')
    index=None
    for _,depot in depot_dict.items():
        if depot.depot_capacity>0:
            in_out_distance=model.distance_matrix[depot.id,route[0]]+model.distance_matrix[route[-1],depot.id]
            if in_out_distance<min_in_out_distance:
                index=depot.id
                min_in_out_distance=in_out_distance
    if index is None:
        print("there is no vehicle to dispatch")
    route.insert(0,index)
    route.append(index)
    depot_dict[index].depot_capacity=depot_dict[index].depot_capacity-1
    return route,depot_dict

def splitRoutes(node_id_list,model):
    num_vehicle = 0
    vehicle_routes = []
    route = []
    remained_cap = model.vehicle_cap
    depot_dict=copy.deepcopy(model.depot_dict)
    for node_id in node_id_list:
        if remained_cap - model.demand_dict[node_id].demand >= 0:
            route.append(node_id)
            remained_cap = remained_cap - model.demand_dict[node_id].demand
        else:
            route,depot_dict=selectDepot(route,depot_dict,model)
            vehicle_routes.append(route)
            route = [node_id]
            num_vehicle = num_vehicle + 1
            remained_cap =model.vehicle_cap - model.demand_dict[node_id].demand

    route, depot_dict = selectDepot(route, depot_dict, model)
    vehicle_routes.append(route)

    return num_vehicle,vehicle_routes

def calRouteDistance(route,model):
    distance=0
    for i in range(len(route)-1):
        from_node=route[i]
        to_node=route[i+1]
        distance +=model.distance_matrix[from_node,to_node]
    return distance

def calObj(node_id_list,model):
    num_vehicle, vehicle_routes = splitRoutes(node_id_list, model)
    if model.opt_type==0:
        return num_vehicle,vehicle_routes
    else:
        distance = 0
        for route in vehicle_routes:
            distance += calRouteDistance(route, model)
        return distance,vehicle_routes

（6）邻域生成
这里在生成邻域时直接借用TS算法中所定义的三类算子。

def createActions(n):
    action_list=[]
    nswap=n//2
    #第一种算子（Swap）：前半段与后半段对应位置一对一交换
    for i in range(nswap):
        action_list.append([1,i,i+nswap])
    #第二中算子（DSwap）：前半段与后半段对应位置二对二交换
    for i in range(0,nswap,2):
        action_list.append([2,i,i+nswap])
    #第三种算子（Reverse）：指定长度的序列反序
    for i in range(0,n,4):
        action_list.append([3,i,i+3])
    return action_list

def doAction(node_id_list,action):
    node_id_list_=copy.deepcopy(node_id_list)
    if action[0]==1:
        index_1=action[1]
        index_2=action[2]
        node_id_list_[index_1],node_id_list_[index_2]=node_id_list_[index_2],node_id_list_[index_1]
        return node_id_list_
    elif action[0]==2:
        index_1 = action[1]
        index_2 = action[2]
        temporary=[node_id_list_[index_1],node_id_list_[index_1+1]]
        node_id_list_[index_1]=node_id_list_[index_2]
        node_id_list_[index_1+1]=node_id_list_[index_2+1]
        node_id_list_[index_2]=temporary[0]
        node_id_list_[index_2+1]=temporary[1]
        return node_id_list_
    elif action[0]==3:
        index_1=action[1]
        index_2=action[2]
        node_id_list_[index_1:index_2+1]=list(reversed(node_id_list_[index_1:index_2+1]))
        return node_id_list_

（7）绘制收敛曲线

def plotObj(obj_list):
    plt.rcParams['font.sans-serif'] = ['SimHei'] #show chinese
    plt.rcParams['axes.unicode_minus'] = False  # Show minus sign
    plt.plot(np.arange(1,len(obj_list)+1),obj_list)
    plt.xlabel('Iterations')
    plt.ylabel('Obj Value')
    plt.grid()
    plt.xlim(1,len(obj_list)+1)
    plt.show()

（8）绘制车辆路线

def plotRoutes(model):
    for route in model.best_sol.routes:
        x_coord=[model.depot_dict[route[0]].x_coord]
        y_coord=[model.depot_dict[route[0]].y_coord]
        for node_id in route[1:-1]:
            x_coord.append(model.demand_dict[node_id].x_coord)
            y_coord.append(model.demand_dict[node_id].y_coord)
        x_coord.append(model.depot_dict[route[-1]].x_coord)
        y_coord.append(model.depot_dict[route[-1]].y_coord)
        plt.grid()
        if route[0]=='d1':
            plt.plot(x_coord,y_coord,marker='o',color='black',linewidth=0.5,markersize=5)
        elif route[0]=='d2':
            plt.plot(x_coord,y_coord,marker='o',color='orange',linewidth=0.5,markersize=5)
        else:
            plt.plot(x_coord,y_coord,marker='o',color='b',linewidth=0.5,markersize=5)
    plt.xlabel('x_coord')
    plt.ylabel('y_coord')
    plt.show()

（9）输出结果

def outPut(model):
    work=xlsxwriter.Workbook('result.xlsx')
    worksheet=work.add_worksheet()
    worksheet.write(0,0,'opt_type')
    worksheet.write(1,0,'obj')
    if model.opt_type==0:
        worksheet.write(0,1,'number of vehicles')
    else:
        worksheet.write(0, 1, 'drive distance of vehicles')
    worksheet.write(1,1,model.best_sol.obj)
    for row,route in enumerate(model.best_sol.routes):
        worksheet.write(row+2,0,'v'+str(row+1))
        r=[str(i)for i in route]
        worksheet.write(row+2,1, '-'.join(r))
    work.close()

（10）主函数

def run(demand_file,depot_file,T0,Tf,deltaT,v_cap,opt_type):
    """
    :param demand_file: 需求节点数据文件
    :param depot_file: 车场节点数据文件
    :param T0: 初始温度
    :param Tf: 终止温度
    :param deltaT: 温度下降步长或下降比例
    :param v_cap: 车辆容量
    :param opt_type: 优化类型:0:最小化车辆数,1:最小化行驶距离
    :return:
    """
    model=Model()
    model.vehicle_cap=v_cap
    model.opt_type=opt_type
    readCsvFile(demand_file,depot_file,model)
    calDistance(model)
    action_list=createActions(len(model.demand_id_list))
    history_best_obj=[]
    sol=Sol()
    sol.node_id_list=genInitialSol(model.demand_id_list)
    sol.obj,sol.routes=calObj(sol.node_id_list,model)
    model.best_sol=copy.deepcopy(sol)
    history_best_obj.append(sol.obj)
    Tk=T0
    nTk=len(action_list)
    while Tk>=Tf:
        for i in range(nTk):
            new_sol = Sol()
            new_sol.node_id_list = doAction(sol.node_id_list, action_list[i])
            new_sol.obj, new_sol.routes = calObj(new_sol.node_id_list, model)
            detla_f=new_sol.obj-sol.obj
            if detla_f<0 or math.exp(-detla_f/Tk)>random.random():
                sol=copy.deepcopy(new_sol)
            if sol.obj<model.best_sol.obj:
                model.best_sol=copy.deepcopy(sol)
        if deltaT<1:
            Tk=Tk*deltaT
        else:
            Tk = Tk - deltaT
        history_best_obj.append(model.best_sol.obj)
        print("当前温度：%s，local obj:%s best obj: %s" % (Tk,sol.obj,model.best_sol.obj))
    plotObj(history_best_obj)
    plotRoutes(model)
    outPut(model)

6. 完整代码

代码和数据文件可获取：

https://download.csdn.net/download/python_n/37365542