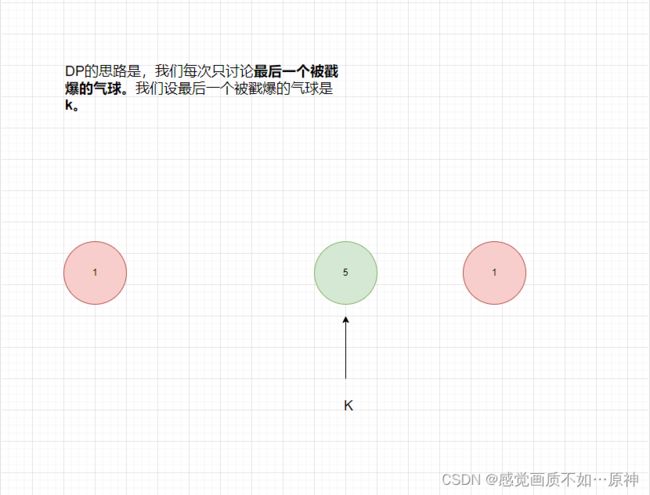
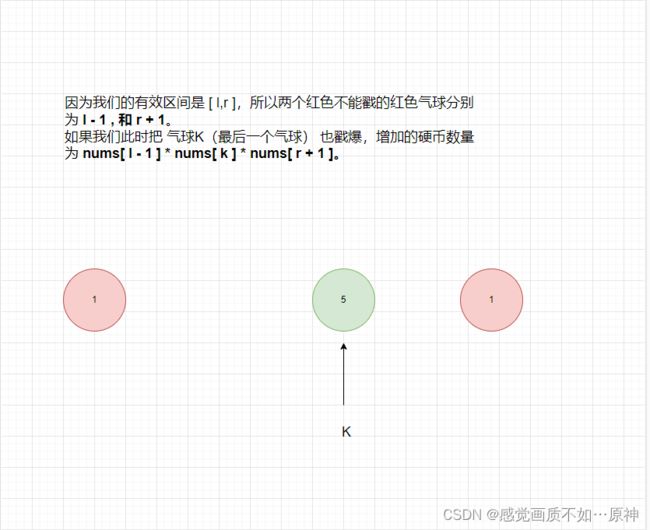
Leetcode.312 戳气球

题目链接

Leetcode.312 戳气球

题目描述

有 n个气球，编号为0到 n - 1，每个气球上都标有一个数字，这些数字存在数组 nums中。

现在要求你戳破所有的气球。戳破第 i 个气球，你可以获得 $nums[i-1]\ast nums[i]\ast nums[i+1]$ 枚硬币。 这里的 i - 1和 i + 1代表和 i相邻的两个气球的序号。如果 i - 1或 i + 1超出了数组的边界，那么就当它是一个数字为 1的气球。

求所能获得硬币的最大数量。

示例 1：

输入：nums = [3,1,5,8]
输出：167
解释：
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3 * 1 * 5 + 3 * 5 * 8 + 1 * 3 * 8 + 1 * 8 * 1 = 167

示例 2：

输入：nums = [1,5]
输出：10

提示：

• $n==nums.length$
• $1<=n<=300$
• $0<=nums[i]<=100$

分析：

本题可以使用 区间DP 的方式求解。我们定义 $f(l,r)$ 为戳爆区间$[l,r]$ 的气球能获得的最多硬币数量。那么我们最终返回的答案就是 $f(1,n)$ （开始在nums 的两边都插入 1，避免处理复杂的边界问题。例如：$nums=[3,1,5,8]$ ，预处理之后为 $nums=[1,3,1,5,8,1]$）

时间复杂度：$O(n^2)$

代码：

class Solution {
public:
    int maxCoins(vector<int>& nums) {
        int n = nums.size();
        //在数组头尾插入1 避免处理边界问题
        nums.insert(nums.begin(),1);
        nums.push_back(1);

        int f[n+5][n+5];
        //f 数组初始化为 0
        memset(f,0,sizeof f);

        //外层循环枚举长度 len
        for(int len = 1;len <= n;len++){
            //内层循环枚举区间的起点 i 和 终点 j
            for(int i = 1;i <= n - len + 1;i++){
                int j = i + len - 1;
                //len == 1 区间只有一个气球 直接戳爆计算
                if(len == 1){
                    f[i][j] = nums[i-1] * nums[i] * nums[i+1];
                    continue;
                }
                else{
                    //枚举 取最大的值
                    for(int k = i;k <= j;k++){
                        f[i][j] = max(f[i][j],f[i][k-1]+f[k+1][j] + nums[i-1] * nums[k] * nums[j+1]);
                    }
                }
            }
        }
        //因为插入头尾两个1之后 nums = [1,...,1] 所以有效区间应该是从下标 1 到 n的
        return f[1][n];
    }
};