瓦片地图服务与地图瓦片原理
本文字数:9099字
预计阅读时间:25分钟
这里,首先我们从概念出发,搞清楚瓦片地图服务以及地图瓦片的原理,读起来似乎有点拗口,但是从字面上看得出它们必定拥有着区别与联系,前者是WebGIS中的一个服务,后者则是关于‘地图瓦片’的底层原理,那么什么是瓦片地图服务呢?
一、瓦片地图服务
根据官方定义,瓦片地图服务(TMS,Tile Map Service)指的是OSGeo的瓦片地图服务规范,提供的操作允许用户按需访问瓦片地图。在OGC标准化服务中,也有一个类似的服务,叫做WMTS(Web Map Tile Service,网络地图瓦片服务),它是OGC提出的缓存技术标准。两者名字虽然不一样,但是都是地图瓦片服务,在本质上非常类似,基本上遵循的是同一种切片规则。所以,这里对这两者不再区分,下述均以WMTS为代表说明。WMTS的产生是为了更高效快速的加载渲染地图数据。如果海量的地图数据以矢量的形式传输到客户端、在客户端渲染,那么我们可以确定的是,首先需要消耗大量的网络流量,其次,这对客户端的CPU/GPU也必定会有较大的负荷。基于这些情况,WMTS提出预渲染图块的模式,在服务端将地图渲染好,并根据比例尺分割不同的栅格图块,根据客户端的请求,传输这些图块,提供给客户端进行展示。所以,也可以简单的理解为,WMTS是WMS“能将切片保存到本地”的版本。目前,大部分PC端、移动端的地图底图使用的基本上都是这种栅格瓦片。
二、地图瓦片原理
那么,到底什么是地图瓦片呢?
2.1 瓦片
将一定范围内的地图按照一定的尺寸和格式,按缩放级别或者比例尺,切成若干行和列的正方形栅格图片,切片后的正方形栅格图片就如同屋顶错落有致的瓦片一样,故被形象的称为瓦片(Tile)。
图1:瓦片(左),地图瓦片(右)
2.2 金字塔模型
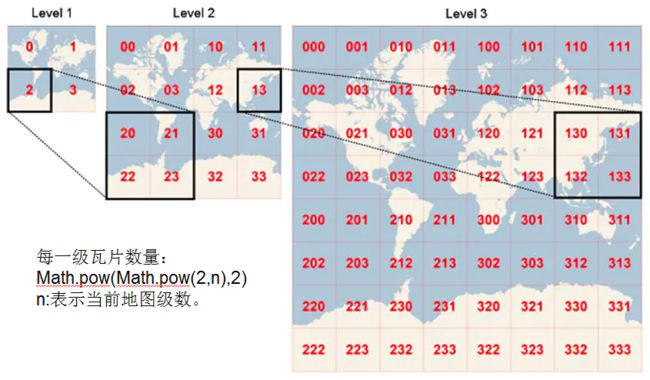
瓦片地图的金字塔模型是一种多分辨率的层次模型,如图二所示,zoom level(瓦片等级)越大,组成地图的瓦片数越多,可以展示的地图内容也就越详细。
图2:地图瓦片层次关系
在某一zoom level下的地图瓦片,是由它的上一层级的各瓦片切割成的4个瓦片组成,如果把这种层级关系自顶向下依次排列,就如同金字塔一样,如图三所示。可以看出,从瓦片金字塔的底层到顶层,分辨率越来越低,但表示的地理范围不变,地图的最小zoom level为0,此时整张地图是一个瓦片。
图3:地图瓦片金字塔模型
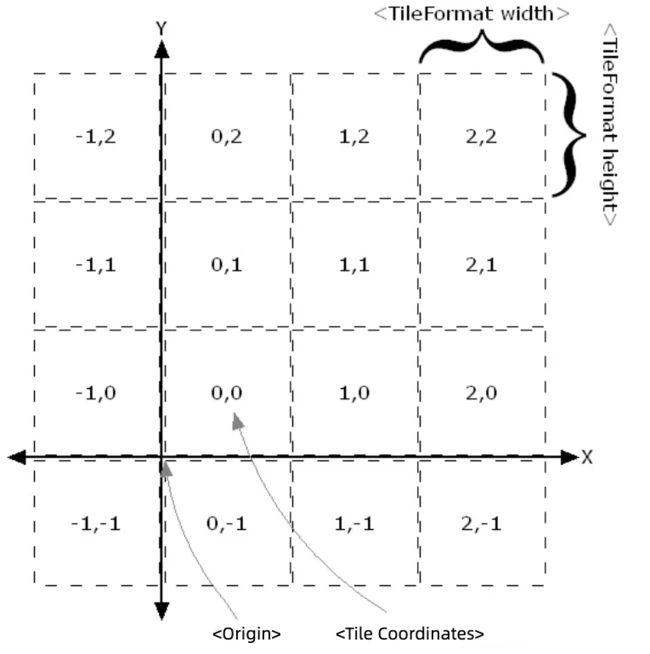
根据WMTS官方标准,规定的瓦片地图设定Web-Mercator投影坐标系原点为东经180°、南纬85.05°,x轴向右,y轴向上,zoom level最小为0,最大为24。瓦片尺寸通常为256*256像素(也可以是其它尺寸)。
图4:WMTS瓦片地图规范
但是在这个标准出台以前,Google的瓦片地图规范已经施行多年,深受行业认可,国内外图商,如OSM、高德、腾讯等都使用Google的瓦片地图规范,其定义略有不同,坐标原点为东经180°、北纬85.05°,x轴向右,y轴向下,zoom level最小为0、最大为21。
图5:Google瓦片地图规范
三、瓦片地图的生产与分发
上述对地图瓦片及瓦片地图服务有了一个概念性的了解,那么接下来,我们一起看一下瓦片地图的整个生产流程是怎样的。在已有数据的前提下,整个流程大概经过三个环节:对地理数据进行投影,并进行配图 ;分层级渲染数据,对渲染后栅格图像进行切片处理;分发地图瓦片,并进行前端展示。
3.1 地图投影与配图
3.1.1 数据投影
在数据库中,地理数据是以地理坐标系(如WGS84)存储的,为了更好地进行展示,那么我们首先需要将这种以经纬度形式存储的三维数据映射到二维平面上。这便是地图投影,它是利用一定数学法则把地球表面的经纬度转换到平面上的理论和方法。
(1)地图坐标系
这里需要理解几个地图中使用的坐标系,以帮助我们理解投影的作用。
地理坐标系,也叫经纬度坐标系。像素坐标系,也可以称为屏幕坐标系。像素坐标系和地理坐标系存在对应关系,屏幕上的每一个像素都对应一个经纬度位置。在瓦片地图服务中,不同的zoom level下,像素坐标系与地理坐标系之间的对应关系是不同的。
投影坐标系,其定义在上面已经给出,既然经纬度能够在二维平面进行表示,那么,就可以在二维平面上对像素坐标系与投影坐标系之间进行映射,这就引出了投影坐标系的一个重要作用:将地理坐标系和屏幕坐标系关联起来。所以,理解投影坐标系是GIS研究中的一个重要环节。
(2)投影方法与分类
由于地球是一个赤道略宽两级略扁的不规则的梨形球体,故其表面是一个不可展平的曲面,所以运用任何数学方法进行这种转换都会产生误差和变形,为了在不同需求下减小误差,就产生了各种投影方法。
图6:地图投影示意及分类
如上图所示,根据投影方法的不同,就形成了不同的投影类型,常见的投影类型有:高斯-克吕格投影、斜轴等面积方位投影、双标准纬线等角圆锥投影、等差分纬线等角圆锥投影、等差分纬线多圆锥投影、正轴方位投影、墨卡托投影等。
(3)墨卡托投影
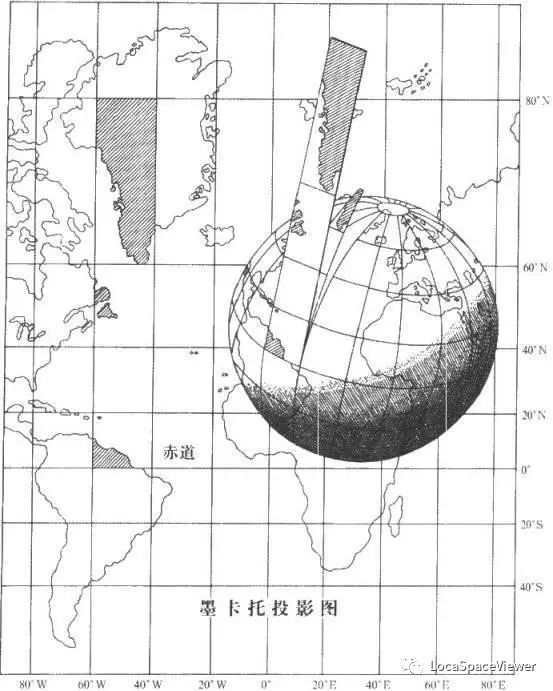
在这诸多地图投影方法中,值得强调的是墨卡托投影。墨卡托投影,是一种正轴等角圆柱投影。由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球,按等角条件,将经纬网投影到圆柱面上,将圆柱面展为平面后,即为墨卡托投影。墨卡托投影没有角度变形,由每一点向各方向的长度比相等,它的经纬线都是平行直线,且相交成直角,经线间隔相等,纬线间隔从标准纬线向两极逐渐增大。墨卡托投影的地图上长度和面积变形明显,但标准纬线无变形,从标准纬线向两极变形逐渐增大,但因为它具有各个方向均等扩大的特性,保持了方向和相互位置关系的正确。在地图上保持方向和角度的正确是墨卡托投影的优点,墨卡托投影地图常用作航海图和航空图,如果循着墨卡托投影图上两点间的直线航行,方向不变可以一直到达目的地,因此它对船舰在航行中定位、确定航向都具有有利条件,给航海者带来很大方便。
图7:墨卡托投影示意图
目前国内做数字城市方面的GIS项目、产品和公众应用,常涉及的投影方式主要有:面向局部区域的二维平面高斯投影(横轴墨卡托,横轴圆柱投影)、面向大范围(如全省、全国)的兰伯特投影(圆锥投影)、面向大范围的经纬度等间隔直投,而互联网上的大部分地图网站(百度地图、Google Maps)则是另外一种——“Web墨卡托”。Web墨卡托是墨卡托投影的变体,较接近于最原始的墨卡托,即正轴墨卡托(投影圆柱的轴心与地球自转轴重合)。由于 Web 墨卡托投影指定了在 WGS 84 椭球面模型上给出的测量坐标,但在投影的时候定义在球面上的,因此会有偏离,但在小比例尺民用场景精度可忽略不计,它主要的优点还是计算简单,数学运算复杂度低。
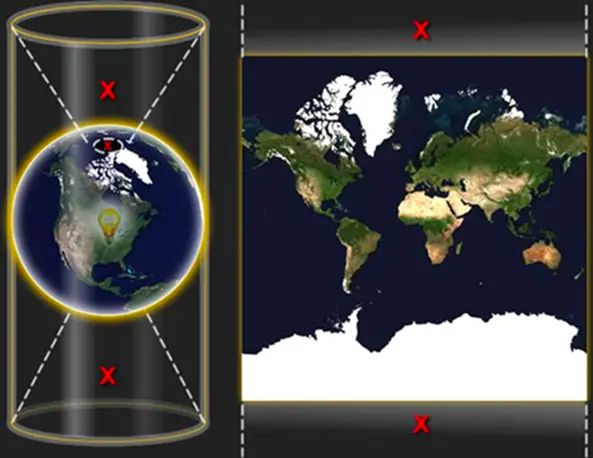
图8:Web墨卡托投影示意图
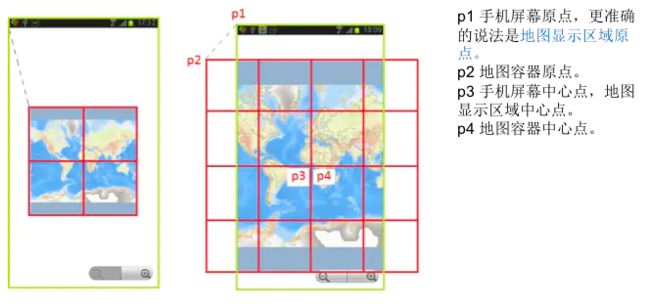
因为将极点投影在无穷远处,所以使用 Web墨卡托投影的地图无法显示极点,数据覆盖范围在经度 (-180°~180°),纬度 (-85.051129°~85.051129°)之间,投影的地图也是正方形。如果在移动端展示一张Web墨卡托投影的地图,通常是将地图中心点固定在移动设备屏幕的中心点,那么效果如下:
图9:手机与地图的位置关系
3.1.2 地图配图
对数据进行投影后,还需要根据数据类型、比例尺级别对数据进行配置、分层级配图。不同的数据类型配置不同的样式,比如不同区域填充不同颜色,铁路显示为黑白相间的线段等;在不同的比例尺级别下,显示的内容详略也会不同,比如在zoom level小于10的时候仅显示省道、国道,大于15的时候显示城市道路等。数据的配图相对比较简单,但是需要关注的细节较多,诸如ArcGIS、QGIS等专业的桌面软件提供了丰富的工具。
3.2 地图切片及瓦片定位
同前文一样,这里以Google地图的TMS规范为例(若无特别说明,本文举例均使用Google规范),梳理地图切片的流程及原理。上一节中,我们对地图投影做了一个大概的了解,根据投影的作用,可以知道想要将经纬度坐标转换为像素坐标,大致过程是:经纬度=>米(英尺)=>像素坐标。在TMS中,我们需要将经纬度坐标转换成瓦片坐标,Web墨卡托投影的转换流程如下图所示。
图10:手机与地图的位置关系
下面我们以Google瓦片规范简单描述一下Web墨卡托投影的算法原理。当缩放等级zoom level等于0时,Web墨卡托投影就是球面投影到一个正方形的平面上,这个平面就是将世界坐标调整为左上角为(0,0),右下角为(256,256)的正方形,假设基本单位为像素,那么就等于把地图投影在一个256pixel*256pixel的图幅上:
x = \lfloor \frac{256}{2\pi} * 2^{zoom\_level}(lng + \pi) \rfloor * pixels
\\
y = \lfloor \frac{256}{2\pi} * 2^{zoom\_level}(\pi - \ln[\tan(\frac{\pi}{4} + \frac{lat}{2})]) * pixels其中x、y是像素坐标,lng、lat是经纬度,pixels是像素,zoom_level是地图瓦片比例尺层级。那么,经纬度坐标转换为瓦片坐标其推导过程为 经纬度 => 米 => 像素坐标 => 瓦片坐标。
3.2.1 地理坐标=>投影坐标(经纬度=>米)
X_{proj} = lng * \frac{2 * \pi * R}{2.0}
\\
Y_{proj} = R * log(tan(\frac{(90+lat)*\pi}{360}))# 地理坐标投影
def LatLongToMeterXY(lng, lat) {
# 地球的周长的一半 20037508.342789244 单位米
circumferenceHalf = math.pi * 2 * 6378137 / 2.0
meterX = lng * circumferenceHalf / 180
temp = math.log(math.tan((90 + lat) * (math.pi / 360.0))) / (math.pi / 180.0)
meterY = circumferenceHalf * temp / 180
return meterX,meterY
# [-20037508.342789244, -20037508.342789244, 20037508.342789244, 20037508.342789244]3.2.2 投影坐标=>像素坐标(米=>像素)
X_{pixel} = \frac{(X_{proj}+\pi*R)*tile_size*z^{zoom}}{2*\pi*R}
\\
Y_{pixel} = \frac{(Y_{proj}+\pi*R)*tile_size*z^{zoom}}{2*\pi*R}# 投影坐标转像素坐标
def metersToPixelXY(meterX, meterY, zoom, tileSize=256) {
# 地球的周长的一半 20037508.342789244 单位米
circumferenceHalf = math.pi * 2 * 6378137 / 2.0
# 米/每像素
resolution = math.pi * 2 * 6378137 / (tileSize * math.pow(2, zoom))
pixelX = (meterX + circumferenceHalf) / resolution
pixelY = (meterY + circumferenceHalf) / resolution
return pixelX,pixelY3.2.3 地理坐标=>像素坐标(经纬度=>像素)
X_{pixel} = \frac{lng+180}{360}*2^z*256 \mod 256
\\
Y_{pixel} = (1-\frac{\ln(\tan(\frac{lat*\pi}{180}) + \sec(\frac{lat * \pi}{180}))}{2* \pi} *2^z*256\mod256# 经纬度转像素
def lnglatToPixel(lng,lat,zoom):
pixelX=round((lng+180)/360*math.pow(2,zoom)*256%256)
pixelY=round((1-math.log(math.tan(math.radians(lat))+1/math.cos(math.radians(lat)))/(2*math.pi))*math.pow(2,zoom)*256%256)
return pixelX,pixelY3.2.4 像素坐标 =>瓦片坐标(像素=>瓦片)
X_{tile} = \lfloor \frac{X_{pixel}}{tile\_size} \rfloor
\\
Y_{tile} = \lfloor \frac{Y_{pixel}}{tile\_size} \rfloordef pixelXYToTileXY(pixelX, pixelY, tileSize=256) {
tileX = Math.floor(pixelX / tileSize)
tileY = Math.floor(pixelY / tileSize)
return tileX,tileY3.2.5 地理坐标<=>瓦片坐标(经纬度<=>瓦片)
(1)地理坐标转瓦片坐标
X_{pixel} = \frac{lng+180}{360}*2^z*256 \mod 256
\\
Y_{pixel} = (1-\frac{\ln(\tan(\frac{lat*\pi}{180}) + \sec(\frac{lat * \pi}{180}))}{2* \pi} *2^z*256\mod256# 经纬度转瓦片
def lnglatToTile(lng,lat,zoom):
tileX=int((lng+180)/360*math.pow(2,zoom))
tileY=int((1-math.asinh(math.tan(math.radians(lat)))/math.pi)*math.pow(2,zoom-1))
return tileX,tileY(2)瓦片坐标转地理坐标
lng = \frac{X_{tile}}{2^z}*360-180
\\
lat = arctan(sinh(\pi*(1-\frac{2*Y_{tile}}{2^z})))*\frac{180}{\pi}# 瓦片转经纬度
def tileToLnglat(tileX,tileY,zoom):
lng=tileX/math.pow(2,zoom)*360-180
lat=math.degrees(math.atan(math.sinh(math.pi*(1-2*tileY/math.pow(2,zoom)))))
return lng,lat(3)瓦片坐标的像素坐标转地理坐标
lng = \frac{X_{tile}+\frac{X_{pixel}}{256}}{2^z}*360-180
\\
lat = arctan(sinh(\pi*(1-\frac{2*(Y_{tile}+{\frac{Y_{pixel}}{256}})}{2^z})))*\frac{180}{\pi}# 瓦片坐标的像素坐标转经纬度
def pixelToLnglat(tileX,tileY,pixelX,pixelY,level):
lng=(tileX+pixelX/256)/math.pow(2,level)*360-180
lat=math.degrees(math.atan(math.sinh(math.pi-2*math.pi*(tileY+pixelY/256)/math.pow(2,level))))
return lng,lat3.3 瓦片分发
瓦片是为了优化数据传输和提升渲染性能。切片后得到的瓦片以金字塔索引形式保存,一般是每个缩放等级为一个独立的目录,其中每列为一个子目录,该子目录中存放该列所有的瓦片文件,故每个瓦片的路径可表示为:缩放等级+列号+行号,例如z/x/y.png的形式。另外,鉴于服务并发考虑,瓦片服务器会提供多个子域以应对大流量问题。比如OSM地图服务:
A 子域名:https://a.tile.openstreetmap.org/12/3371/1551.png
B 子域名:https://b.tile.openstreetmap.org/12/3371/1551.png
C 子域名:https://c.tile.openstreetmap.org/12/3371/1551.png
图11:OSM瓦片示例
通过上面的URL以及瓦片路径结构,可以看出上图中的瓦片来自于缩放等级为12,第3771列、第1551行。可以概括的看这个URL结构为:
https://{sub_domain}.tile.openstreetmap.org/{z}/{x}/{y}.png那么,瓦片的分发其实就是把这些瓦片文件通过静态文件服务器或者CDN以诸如这种形式发布出去,客户端就可以获取这些瓦片,并通过相应的目录结构拼接渲染完整的地图。
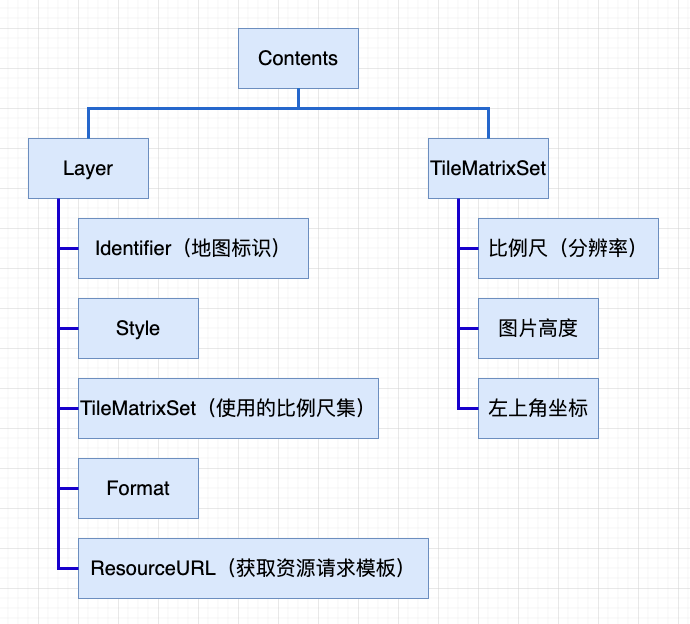
3.4 瓦片地图服务解析
瓦片地图的展示,简单的讲,就是网格平铺,并根据瓦片序号装载对应瓦片的过程。整个流程可以简单概括为:获取目标地图的地理范围和缩放等级,计算瓦片坐标;通过服务地址、瓦片坐标,获取瓦片数据;拼接渲染;
3.4.1 瓦片地图服务解析流程
为了更好的理解瓦片地图服务的解析流程,下面以L7栅格与矢量瓦片服务的解析设计流程为例,理解客户端是如何获取瓦片并渲染成全部地图的。
图12:L7栅格与矢量瓦片服务的解析流程
3.4.2 leaflet中实现瓦片的渲染
下面在leaflet中对实现上述逻辑,以便更清晰的理解整个渲染流程。第一步,我们需要一个DIV容器来装载地图,设定中心坐标和缩放等级,并根据缩放等级、中心坐标、DIV容器的尺寸计算地理空间覆盖范围,进而计算出需要加载多少瓦片以及加载哪些瓦片。然后,在这个DIV中创建一些与瓦片尺寸一致的DOM,根据像素坐标与地理坐标的对应关系,计算出DOM与瓦片的关系,拼接完整的URL获取瓦片,并将瓦片图像加载到DOM中。最后,通过DOM将瓦片拼接进行展示。
瓦片原理-OSM
四、总结
通过对瓦片服务以及瓦片的原理有了一个大致的理解,在实际应用中就更加得心应手,碰到疑难杂症或者某些需要优化的点的时候,也就有了切入口,甚至是会有更深的见解,知其然,也知其所以然。当然,纸上得来终觉浅,绝知此事要躬行,理论必须付诸实践才能发挥出其深层次的意义。
参考文献
[1]https://baike.baidu.com/item/%E5%A2%A8%E5%8D%A1%E8%A8%97%E6%8A%95%E5%BD%B1/5477927
[2]https://wiki.openstreetmap.org/wiki/Slippy_map_tilenames
[3]https://www.yuque.com/antv/l7/up4re5
[4]http://webgis.cn/standard-wmts.html
[5]https://github.com/antvis/L7/tree/master/packages/utils/src/tileset-manager