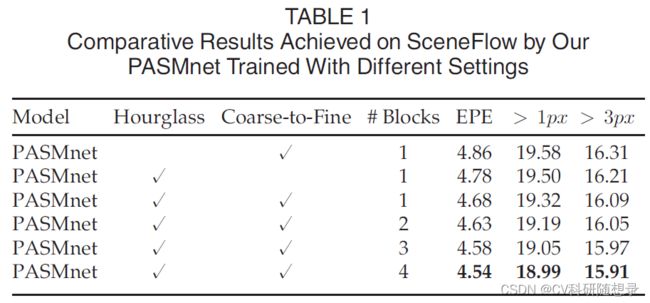
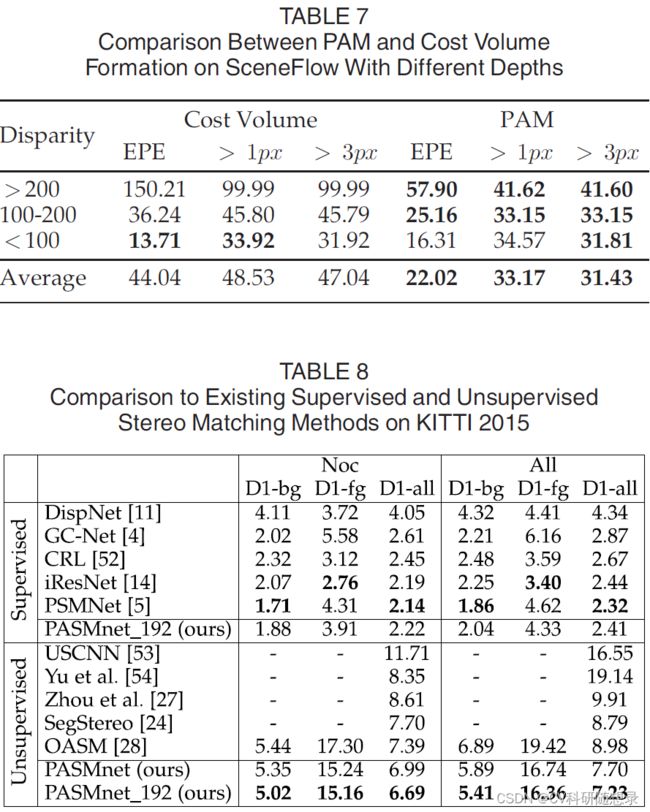
论文阅读《Parallax Attention for Unsupervised Stereo Correspondence Learning》

论文地址：https://ieeexplore.ieee.org/document/9206116
源码地址：https://github.com/The-Learning-And-Vision-Atelier-LAVA/PAM

---

概述

  不同数据集的视图之间的基线、焦距与分辨率不同，基于Cost Volume固定预设视差范围的立体匹配方法无法很好处理大视差预测问题。为此，作者提出一个基于视差注意力机制的立体匹配方法来捕捉大视差范围的匹配点的信息，通过将极线约束与注意力机制结合，计算沿着极线方向的特征相似度来获取匹配点之间的匹配关系。

---

模型架构

Formulation：在图像自注意力机制中，将特征图从 ${\mathbb{R}}^{H\times W\times C}$ 转换为 ${\mathbb{R}}^{HW\times C}$ 后进行矩阵相乘( ${\mathbb{R}}^{HW\times C}\times {\mathbb{R}}^{C\times HW}$ )来得到像素之间的注意力。受到自注意力机制的启发，PAM 基于极限约束来求左右视图极线之间的注意力，如图3所示：

  给定左右特征图 $A,B\in {\mathbb{R}}^{\mathbb{H}\times \mathbb{W}\times \mathbb{C}}$，使用 $1\times 1$ 的卷积进行特征通道融合，继而进行维度转换得 $Q\in {\mathbb{R}}^{\mathbb{H}\times \mathbb{W}\times \mathbb{C}}$ 与 $K\in {\mathbb{R}}^{\mathbb{H}\times \mathbb{C}\times \mathbb{W}}$。将 $Q$ 与 $K$ 矩阵相乘后经过softmax层得到极线注意力图 $M_{B⟶A\in \mathbb{H}\times \mathbb{W}\times \mathbb{W}}$。将 B 经过另外一个 $1\times 1$ 卷积层后得到 $\mathbf{R}\in {\mathbb{R}}^{H\times W\times C}$，然后将 $M_{B⟶A}\in \mathbb{H}\times \mathbb{W}\times \mathbb{W}$ 与 $\mathbf{R}$ 相乘后得到输出特征图 $O\in {\mathbb{R}}^{H\times W\times C}$，同时使用 $M_{B⟶A}\in \mathbb{H}\times \mathbb{W}\times \mathbb{W}$ 生成 Mask $V_B$。

示例：给定尺寸为 $30\times 30$ 的左右图像 ${\mathbf{I}}_{left}$ 与 ${\mathbf{I}}_{right}$，可以使用PAM来生成对应的视差注意力图 $M_{left⟶right}$ 与 $M_{right⟶left}\in {\mathbb{R}}^{30\times 30\times 30}$。

  其中，图4中第一行为左右视差图，第二行为对应的视差注意力图，图4(a)或图4(b)中的视差注意力图的第一列为$M_{right⟶left}$，其中横方向为右图的索引，纵轴为左图的索引，现在只考虑黄线(左右图像的第 $i$ 行)，。如果左右图像是完全匹配的（视差为0），则生成的注意力图像如图4(a) 第二行所示，只有对角线上的元素为1，即$M_{right⟶left}(i,j,j)=1$，代表左图第$i$ 行的第$j$ 个像素${\mathbf{I}}_{left}(i,j)$ 与 右图第$i$ 行第$j$ 个像素${\mathbf{I}}_{right}(i,j)$ 匹配上了。在视差不为0的区域，图4(b)所示，如视差为5的区域，表示左图第$i$ 行的第$j$ 个像素${\mathbf{I}}_{left}(i,j)$ 与 右图第$i$ 行第$j-5$ 个像素${\mathbf{I}}_{right}(i,j-5)$ 匹配上了，即$M_{right⟶left}(i,j,j-5)=1$。
  同时可以从视差注意力图中得到遮挡图，如图4(b) 第一列中，某些列中没有激活点，说明在右图中的 $j$ 点在左图中没有匹配点，即该点在左图中被遮挡。如果某一行没有激活点，则导表该点在右图中没有匹配点，在右图中被遮挡。

左右一致性与循环一致性：为了得到可靠的一致性匹配结果，使用左右一致性与循环一致性来对PAM模块进行正则化。给定左右视图 ${\mathbf{I}}_{left}$ 与 ${\mathbf{I}}_{right}$ 与 $M_{left⟶right}$ 与 $M_{right⟶left}$，有：
$$\{\begin{array}{rl}{\mathbf{I}}_{\text{left }}& ={\mathbf{M}}_{\text{right }\to \text{ left }}\otimes {\mathbf{I}}_{\text{right }},\\ {\mathbf{I}}_{\text{right }}& ={\mathbf{M}}_{\text{left }\to \text{ right }}\otimes {\mathbf{I}}_{\text{left }}\end{array}\text{\hspace{1em}(1)}$$
其中 $\otimes$ 表示带有几何感知的矩阵乘法，同理，循环一致性表示为：
$$\{\begin{array}{rl}{\mathbf{I}}_{\text{left }}& ={\mathbf{M}}_{\text{left }\to \text{right }\to \text{ left }}\otimes {\mathbf{I}}_{\text{left }},\\ {\mathbf{I}}_{\text{right }}& ={\mathbf{M}}_{\text{right }\to \text{left }\to \text{ right }}\otimes {\mathbf{I}}_{\text{right}}\end{array}\text{\hspace{1em}(2)}$$
其中循环注意力图计算如下：
$$\{\begin{array}{rl}{\mathbf{M}}_{\text{left }\to \text{ right }\to left}& ={\mathbf{M}}_{\text{right }\to \text{ left }}\otimes {\mathbf{M}}_{\text{left }\to \text{ right }}\\ {\mathbf{M}}_{\text{right }\to \text{ left }\to \text{ right }}& ={\mathbf{M}}_{\text{left }\to \text{ right }}\otimes {\mathbf{M}}_{\text{right }\to \text{ left }}\end{array}\text{\hspace{1em}(3)}$$
其中，$\otimes$ 表示矩阵乘法，对于第 $i$ 行，${\mathbf{M}}_{\text{right }\to \text{ left }}(i,:,:)\in {\mathbb{R}}^{W\times W}$与 ${\mathbf{I}}_{right}(i,:,:)\in \mathbb{W}\times \mathbb{C}$ 相乘的结果为第 $i$ 行的每个特征，将 $W$ 行的结果拼接得到 ${\mathbf{I}}_{left}\in {\mathbb{R}}^{H\times W\times C}$。

有效值掩码：左右一致性与循环一致性都未包含遮挡区域的信息，文中使用视差注意力图来生成有效区域掩码，只在有效区域进行正则化，有效掩码如下图所示：
$${\mathbf{V}}_{\text{left }}(i,k)=\{\begin{array}{ll}1,& \text{ if }{\sum }_{j\in [1,W]}{\mathbf{M}}_{left\to right}(i,j,k)>\tau \\ 0,& \text{ otherwise }\end{array}\text{\hspace{1em}(4)}$$

层叠式视差-注意力模块

  层叠注意力模块包含3个stages，每个stage包含4个视差注意力blocks，如图7(b)所示：

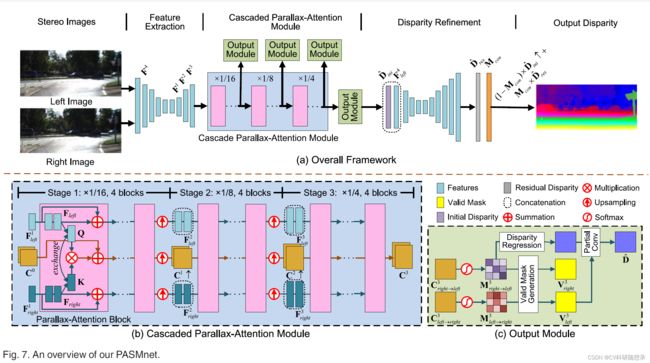
   通过沙漏网络提取到的左右视图的特征图大小为 ${\mathbf{F}}_{\mathbf{left}}^1$ ，${\mathbf{F}}_{\mathbf{right}}^1\in {\mathbb{R}}^{\frac{H}{16}\times \frac{W}{16}\times C}$与初始代价 $C_{right\to left}^0$，$C_{right\to left}^0\in {\mathbb{R}}^{\frac{H}{16}\times \frac{W}{16}\times \frac{W}{16}}$ (初始化为0)。使用 $3\times 3$ 的卷积处理 ${\mathbf{F}}_{left}^l$ 与 ${\mathbf{F}}_{right}^l$ 后得到 ${\mathbf{F}}_{left}$ 与 ${\mathbf{F}}_{right}$。然后使用 $1\times 1$ 的卷积层处理 ${\mathbf{F}}_{left}$ 与 ${\mathbf{F}}_{right}$ 后得到 $\mathbf{Q}$ 与 $\mathbf{K}$, reshape后相乘得到 $C_{right\to left}^1\in {\mathbb{R}}^{\frac{H}{16}\times \frac{W}{16}\times \frac{W}{16}}$。交换${\mathbf{F}}_{\mathbf{left}}^1$ ，${\mathbf{F}}_{\mathbf{right}}^1$ 后生成 $C_{left\to right}^1\in {\mathbb{R}}^{\frac{H}{16}\times \frac{W}{16}\times \frac{W}{16}}$。如图7(b) 所示，将生成的结果送入后续的block中继续生成新的特征图与 $C$。在每个stage之后进行双线性插值到上一层后继续迭代。得到最后的得分矩阵 $C^3$。
   模型通过层叠式视差-注意力模块完成隐式正则化，如图8所示:

  为了简化分析，在此过程中只考虑 $3\times 3$ 的卷积操作。在第 $m^{th}$ 的视差注意力 block 中， 左右视图${\mathbf{f}}_{left}^5$ 与 ${\mathbf{f}}_{right}^5$之间cost $c_{5,5}^m$ 计算如式5所示：
$$\begin{array}{rl}{c}_{5,5}^m& =c_{5,5}^{m-1}+{\left({\mathbf{w}}_Q^m{\mathbf{f}}_{\text{left }}^5\right)}^{\mathrm{T}}{\mathbf{w}}_K^m{\mathbf{f}}_{\text{right }}^5\\ & =c_{5,5}^{m-1}+{\left({\mathbf{f}}_{\text{left }}^5\right)}^{\mathrm{T}}{\left({\mathbf{w}}_Q^m\right)}^{\mathrm{T}}{\mathbf{w}}_K^m{\mathbf{f}}_{\text{right }}^5,\\ & =c_{5,5}^{m-1}+{\Psi }^m\left({\mathbf{f}}_{\text{left }}^5,{\mathbf{f}}_{\text{right }}^5\right)\end{array}\text{\hspace{1em}(5)}$$
其中 $w_Q^m$, $w_K^m\in {\mathbb{R}}^{C\times C}$ 为 $1\times 1$ 的卷积层，${\mathbf{f}}_{left}^5$ 与 ${\mathbf{f}}_{right}^5\in {\mathbb{R}}^{C\times 1}$ 为匹配点的特征。 ${\Psi }^m$ 为输入特征对之间的匹配代价。在 $(m+1{)}^{th}$ 层block的特征向量由第 $m^{th}$ 层特征向量${\mathbf{f}}_{left}$ 与 ${\mathbf{f}}_{right}$的局部邻域聚合而来：
$$\{\begin{array}{rl}{\mathbf{f}}_{\text{left }}& ={\sum }_{i=1}^9{\mathbf{w}}^i{\mathbf{f}}_{\text{left }}^i\\ {\mathbf{f}}_{\text{right }}& ={\sum }_{j=1}^9{\mathbf{w}}^j{\mathbf{f}}_{\text{right }}^j\end{array},\text{\hspace{1em}(6)}$$
其中 ${\mathbf{w}}^i$ 与 ${\mathbf{w}}^j\in {\mathbb{R}}^{C\times C}$ 为权值共享的 $3\times 3$ 的卷积操作。${\mathbf{f}}_{left}$ 与 ${\mathbf{f}}_{right}\in {\mathbb{R}}^{C\times C}$为输出特征向量，匹配代价计算如式7所示：
$$\begin{array}{rl}{c}_{5,5}^{m+1}& =c_{5,5}^m+{\left({\mathbf{w}}_Q^{m+1}{\mathbf{f}}_{\text{left }}\right)}^{\mathrm{T}}{\mathbf{w}}_K^{m+1}{\mathbf{f}}_{\text{right }}\\ & =c_{5,5}^m+\sum _i\sum _j{\left({\mathbf{w}}_Q^{m+1}{\mathbf{w}}^i{\mathbf{f}}_{\text{left }}^i\right)}^{\mathrm{T}}{\mathbf{w}}_K^{m+1}{\mathbf{w}}^j{\mathbf{f}}_{\text{right }}^j\\ & =c_{5,5}^m+\sum _i\sum _j{\left({\mathbf{f}}_{left}^i\right)}^{\mathrm{T}}{\left({\mathbf{w}}^i\right)}^{\mathrm{T}}{\left({\mathbf{w}}_Q^{m+1}\right)}^{\mathrm{T}}{\mathbf{w}}_K^{m+1}{\mathbf{w}}^j{\mathbf{f}}_{\text{right }}^j,\\ & =c_{5,5}^m+\sum _i\sum _j{\Psi }_{i,j}^{m+1}\left({\mathbf{f}}_{left}^i,{\mathbf{f}}_{\text{right }}^j\right)\end{array}\text{\hspace{1em}(7)}$$
求中 ${\mathbf{w}}_Q^{m+1}$, ${\mathbf{w}}_K^{m+1}\in {\mathbb{R}}^{C\times C}$ 为两个 $1\times 1$ 的卷积层。 ${\Psi }_{i,j}^{m+1}(.)$ 为输入特征对之间的匹配代价。从事7中可以看出，在从 $m^{th}$ 到 $m^{th+1}$ 层的过程中完成了隐式的代价聚合。

视差回归

由stage 3 得到的${\mathbf{C}}_{right\to left}^3$ 和 ${\mathbf{C}}_{left\to right}^3$ 经过softmax层得 ${\mathbf{M}}_{right\to left}^3$ 和 ${\mathbf{M}}_{left\to right}^3\in {\mathbb{R}}^{\frac{H}{4}\times \frac{W}{4}\times \frac{W}{4}}$, 如图7（c）所示。继而使用${\mathbf{M}}_{left\to right}^3$, ${\mathbf{M}}_{right\to left}^3$ 生成有效值掩码 ${\mathbf{V}}_{left}^3$ 和 ${\mathbf{V}}_{right}^3$，最后回归视差值：
$$\hat{\mathbf{D}}=\sum _{k=0}^{W/4-1}k\times {\mathbf{M}}_{\text{right }}^3\text{ left }(:,:,k)\text{\hspace{1em}(8)}$$

视差细化

  如图7a所示，使用初始视差值 $\hat{\mathbf{D}}$ 与 ${\mathbf{F}}_{left}^4$ 拼接后送入沙漏网络中生成视差的残差图 ${\hat{\mathbf{D}}}_{res}$ 与置信度图 ${\mathbf{M}}_{con}$:
$${\hat{\mathbf{D}}}_{\text{refined }}=\left(1-{\mathbf{M}}_{\text{con }}\right)\times {\hat{\mathbf{D}}}_{\text{ini }}\uparrow +{\mathbf{M}}_{\text{con }}\times {\hat{\mathbf{D}}}_{\text{res }}\text{\hspace{1em}(9)}$$
其中 $\uparrow$ 为上采样操作。

---

损失函数

光度损失：

L p = 1 N ∑ p ∈ V left  α 1 − S ( I l e f t ( p ) , I ^ ( p ) ) 2 + ( 1 − α ) ∥ I left  ( p ) − I ^ ( p ) ∥ 1 , (10) \mathcal{L}_{\mathrm{p}}=\frac{1}{N} \sum_{p \in \mathbf{V}_{\text {left }}} \alpha \frac{1-\mathcal{S}\left(\mathbf{I}_{l e f t}(p), \hat{\mathbf{I}}(p)\right)}{2}+(1-\alpha)\left\|\mathbf{I}_{\text {left }}(p)-\hat{\mathbf{I}}(p)\right\|_{1},\tag{10} Lp​=N1​p∈Vleft ​∑​α21−S(Ileft​(p),I^(p))​+(1−α) ​Ileft ​(p)−I^(p) ​1​,(10)

平滑损失：

L s = 1 N ∑ p ( ∥ ∇ x D ^ refined  ( p ) ∥ 1 e − ∥ ∇ x I l e f t ( p ) ∥ 1 + ∥ ∇ y D ^ refined  ( p ) ∥ 1 e − ∥ ∇ y I l e f t ( p ) ∥ 1 ) , (11) \begin{array}{l} \mathcal{L}_{\mathrm{s}}= \frac{1}{N} \sum_{p}\left(\left\|\nabla_{x} \hat{\mathbf{D}}_{\text {refined }}(p)\right\|_{1} e^{-\left\|\nabla_{x} \mathbf{I}_{l e f t}(p)\right\|_{1}}\right. \\ +\left\|\nabla_{y} \hat{\mathbf{D}}_{\text {refined }}(p)\right\|_{1} e^{\left.-\left\|\nabla_{y} \mathbf{I}_{l e f t}(p)\right\|_{1}\right),} \end{array}\tag{11} Ls​=N1​∑p​( ​∇x​D^refined ​(p) ​1​e−∥∇x​Ileft​(p)∥1​+ ​∇y​D^refined ​(p) ​1​e−∥∇y​Ileft​(p)∥1​),​(11)

PAM Loss：

   使用3个额外的损失来对不同尺度下的PAM模块正则化：
$${\mathcal{L}}_{\text{PAM }}^s={\mathcal{L}}_{\text{PAM-p }}^s+{\lambda }_{\text{PAM-s }}{\mathcal{L}}_{\text{PAM-s }}^s+{\lambda }_{\text{PAM-c }}{\mathcal{L}}_{\text{PAM-c }}^s.\text{\hspace{1em}(12)}$$

  基于视差注意力图的光度一致性损失：
L PAM-p  s = 1 N left  s ∑ p ∈ V left  s ∥ I left  s ( p ) − ( M right  →  eft  s ⊗ I right  s ) ( p ) ∥ 1 + 1 N right  s ∑ p ∈ V right  s ∥ I right  s ( p ) − ( M left  → r i g h t s ⊗ I left  s ) ( p ) ∥ 1 . (13) \begin{aligned} \mathcal{L}_{\text {PAM-p }}^{s}= & \frac{1}{N_{\text {left }}^{s}} \sum_{p \in \mathbf{V}_{\text {left }}^{s}}\left\|\mathbf{I}_{\text {left }}^{s}(p)-\left(\mathbf{M}_{\text {right } \rightarrow \text { eft }}^{s} \otimes \mathbf{I}_{\text {right }}^{s}\right)(p)\right\|_{1} & +\frac{1}{N_{\text {right }}^{s}} \sum_{p \in \mathbf{V}_{\text {right }}^{s}}\left\|\mathbf{I}_{\text {right }}^{s}(p)-\left(\mathbf{M}_{\text {left } \rightarrow r i g h t}^{s} \otimes \mathbf{I}_{\text {left }}^{s}\right)(p)\right\|_{1} . \end{aligned}\tag{13} LPAM-p s​=​Nleft s​1​p∈Vleft s​∑​ ​Ileft s​(p)−(Mright → eft s​⊗Iright s​)(p) ​1​​+Nright s​1​p∈Vright s​∑​ ​Iright s​(p)−(Mleft →rights​⊗Ileft s​)(p) ​1​.​(13)

  基于视差注意力图的平滑性损失：
$$\begin{array}{rlr}{\mathcal{L}}_{\mathrm{PAM}-\mathrm{s}}^s=& \frac{1}{N^s}\sum _{{\mathbf{M}}^s}\sum _{i,j,k}({\Vert {\mathbf{M}}^s(i,j,k)-{\mathbf{M}}^s(i+1,j,k)\Vert }_1& +{\Vert {\mathbf{M}}^s(i,j,k)-{\mathbf{M}}^s(i,j+1,k+1)\Vert }_1),\end{array}\text{\hspace{1em}(14)}$$

  循环一致性损失：
L P A M − c s = 1 N left  s ∑ p ∈ V left  s ∥ M left  → r i g h t → l e f t s ( p ) − I s ( p ) ∥ 1 + 1 N right  s ∑ p ∈ V right  s ∥ M right  →  left  → r i g h t s ( p ) − I s ( p ) ∥ 1 , (15) \begin{aligned} \mathcal{L}_{\mathrm{PAM}-\mathrm{c}}^{s}= & \frac{1}{N_{\text {left }}^{s}} \sum_{p \in \mathbf{V}_{\text {left }}^{s}}\left\|\mathbf{M}_{\text {left } \rightarrow r i g h t \rightarrow l e f t}^{s}(p)-I^{s}(p)\right\|_{1} & +\frac{1}{N_{\text {right }}^{s}} \sum_{p \in \mathbf{V}_{\text {right }}^{s}}\left\|\mathbf{M}_{\text {right } \rightarrow \text { left } \rightarrow r i g h t}^{s}(p)-I^{s}(p)\right\|_{1}, \end{aligned}\tag{15} LPAM−cs​=​Nleft s​1​p∈Vleft s​∑​ ​Mleft →right→lefts​(p)−Is(p) ​1​​+Nright s​1​p∈Vright s​∑​ ​Mright → left →rights​(p)−Is(p) ​1​,​(15)

$$\begin{array}{rl}{\mathcal{L}}_{\text{unsup }}=& {\mathcal{L}}_{\mathrm{p}}+{\lambda }_{\mathrm{s}}{\mathcal{L}}_{\mathrm{s}}+{\lambda }_{\text{PAM }}\left(0.2{\mathcal{L}}_{\text{PAM }}^1+0.3{\mathcal{L}}_{\text{PAM }}^2+0.5{\mathcal{L}}_{\text{PAM }}^3\right).\end{array}\text{\hspace{1em}(16)}$$

---

实验结果