十大经典排序算法（C语言实现）

前言

---

本文代码链接：十大经典排序算法
提取码：2ok3

排序算法是《数据结构与算法》的重要组成部分，在项目实践中，很多时候都需要用到排序算法，而常见的经典排序算法也是很多公司程序员面试的重点。十大经典排序算法如下图所示。

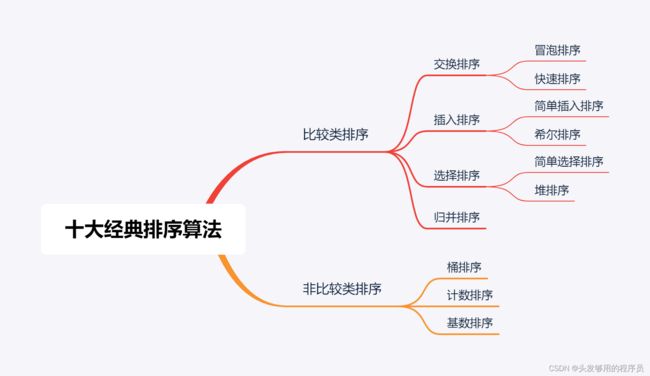
时间复杂度和空间复杂度是衡量一个算法性能好坏的重要指标。而对于排序算法而言，稳定性也是重要指标之一。

教材上给了非常严谨且抽象的定义。

假设ki=kj(1<=i<=n,1<=j<=n,i≠j),且在排序前的序列中ri领先于rj，若果排序后ri仍然领先于rj，则称所用的排序方法是稳定的；反之，若可能使得排序后的序列中rj领先于ri，则称所用的排序方法是不稳定的。

通俗地说，有时候在原序列中两个数值是相等的，如果排序后可以保证原来的相对位置不变，则称该算法是稳定的，若不能保证，则算法是不稳定的。

关于算法的时间复杂度，空间复杂度，稳定性，见下面表格。

1 冒泡排序

冒泡排序是一种交换排序，其基本思想是：两两比较相邻记录的关键字，如果相反则交换，直到没有反序的记录为止。

因较小的数字如同气泡一般慢慢浮到上面，故而得名冒泡排序。

1.1 最简单的排序算法

代码如下：

#include 
#define MAXSIZE 10000
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
void Bubblesort0(sqList* L)
{
	for (int i = 0; i < L->length; i++)
	{
		for (int j = i; j < L->length; j++)
		{
			if (L->r[i] > L->r[j])
				swap(L, i, j);
		}
	}
}
int main()
{
	sqList test = {{9,1,5,8,3,7,4,6,2}, 9};
	Bubblesort0(&test);
	for (int i = 0; i < test.length; i++)
		printf("%d\t", test.r[i]);
 return 0;
}

以上是最简单的冒泡排序算法的实现，每次循环保证得到该范围内的最小值，排在前面，从而完成排序。如图所示：

然而还有改进的空间。是否可在每次循环的时候，比较更多的关键字呢？于是有了改进版的冒泡排序。

1.2 冒泡排序算法

通过以上的改进思路，可以得到一下的代码。

#include 
#define MAXSIZE 10000
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
void Bubblesort1(sqList* L)
{
	for (int i = 0; i < L->length; i++)
	{
		for (int j = L->length - 2; j >= i; j--)
		{
			if (L->r[j] > L->r[j+1])
				swap(L, j, j + 1);
		}
	}
}
int main()
{
	sqList test = {{9,1,5,8,3,7,4,6,2}, 9};
	Bubblesort1(&test);
	for (int i = 0; i < test.length; i++)
		printf("%d\t", test.r[i]);
 return 0;
}

通过以上的改进，在每次循环时，可以比较相邻的关键字，从而变得更加高效。如下图所示：

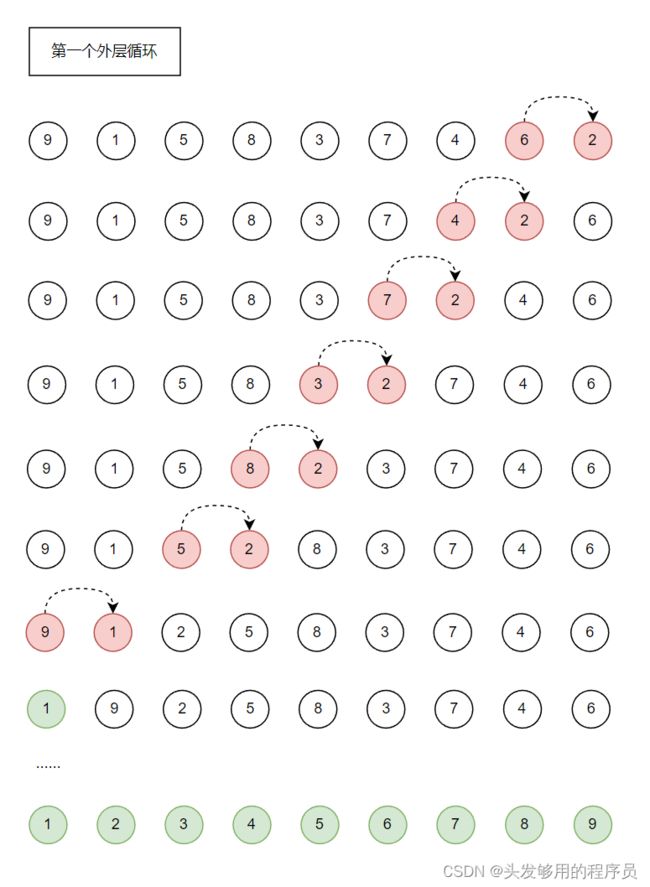
从上图可以看出，一次循环就可以比较更多的数值。所以是个更好的方法。

1.3 冒泡排序算法优化

上面的例子虽然是正宗的冒泡排序算法，但是仍然有改进的空间，如果能在需要排序的数组有序的时候停止循环，肯定会更加高效，于是有了下面的代码。

#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
void Bubblesort2(sqList* L)
{
	short flag = TRUE;
	for (int i = 0; i < L->length && flag; i++)
	{
		flag = FALSE;
		for (int j = L->length - 2; j >= i; j--)
		{
			if (L->r[j] > L->r[j + 1])
			{
				swap(L, j, j + 1);
				flag = TRUE;
			}
		}
	}
}
int main()
{
	sqList test = {{9,1,5,8,3,7,4,6,2}, 9};
	Bubblesort2(&test);
	for (int i = 0; i < test.length; i++)
		printf("%d\t", test.r[i]);
 return 0;
}

这样一来就避免了无意义的循环，如果上次发现算法已经完成了排序，程序就不会进入循环，从而提前结束运行，完成排序任务。

1.4 冒泡排序算法总结

冒泡算法是最常用的算法之一，也是最简单的排序算法之一，但却不是最高效的，以下将介绍其他几种排序算法。

2 选择排序

选择排序的方法也非常好理解，但它并不像冒泡排序一样，遇到顺序不合适的就直接调换位置，而是记录下最小关键字的位置，待循环完毕后再将其与此次循环的第一个关键字的位置做调换，从而保证了每次循环都可以得到该范围内的最小值，故而得名选择排序。

2.1 选择排序的代码实现

具体的实现代码如下。

#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
void SelectSort(sqList *L)
{
	int i, j, min;
	for (i = 0; i < L->length; i++)
	{
		min = i;
		for (j = i + 1; j < L->length; j++)
		{
			if (L->r[min] > L->r[j])
				min = j;
		}
		if (i != min)
			swap(L, i, min);
	}
}
int main()
{
	sqList test = {{9,1,5,8,3,7,4,6,2}, 9};
	SelectSort(&test);
	for (int i = 0; i < test.length; i++)
	printf("%d\t", test.r[i]);
	return 0;
}

通俗地理解，就是不轻易“出手”，外部循环一次，最多调换一次，所以相比冒泡排序稍微高效一些。选择排序的过程如下图所示：

2.2 选择排序算法总结

虽然选择排序比冒泡排序高效一些，但仍然是n²的时间复杂度。

3 插入排序

插入排序又叫直接插入排序或者简单插入排序，这样称呼其实是为了与希尔排序进行区分，其实是同一种排序算法。

所谓插入排序，是将一个记录插入到已经排好序的有序表中，从而得到一个新的，记录数值增1的有序表。

3.1 插入排序的代码实现

插入排序的具体代码如下所示。

注意在插入排序中有个辅助空间，所以数组的第一个元素值为0，排序后的值无效。

#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void InsertSort(sqList *L)
{
	int i, j;
	for (i = 2; i < L->length; i++)
	{
		if (L->r[i] < L->r[i - 1])
		{
			L->r[0] = L->r[i];
			for (j = i - 1; L->r[j] > L->r[0]; j--)
				L->r[j + 1] = L->r[j];
			L->r[j + 1] = L->r[0];
		}
	}
}
int main()
{
	sqList test = {{0,9,1,5,8,3,7,4,6,2}, 10};
	InsertSort(&test);
	for (int i = 0; i < test.length; i++)
	printf("%d\t", test.r[i]);
	return 0;
}

插入排序的算法思想可简单理解为，首先确定需要排序的关键字，然后再放到整个数组的第一个位置，再将其放回原数组中，放回的时候进行排序，但只保证该位置及其前面关键字的相对位置没有问题。
如图所示：

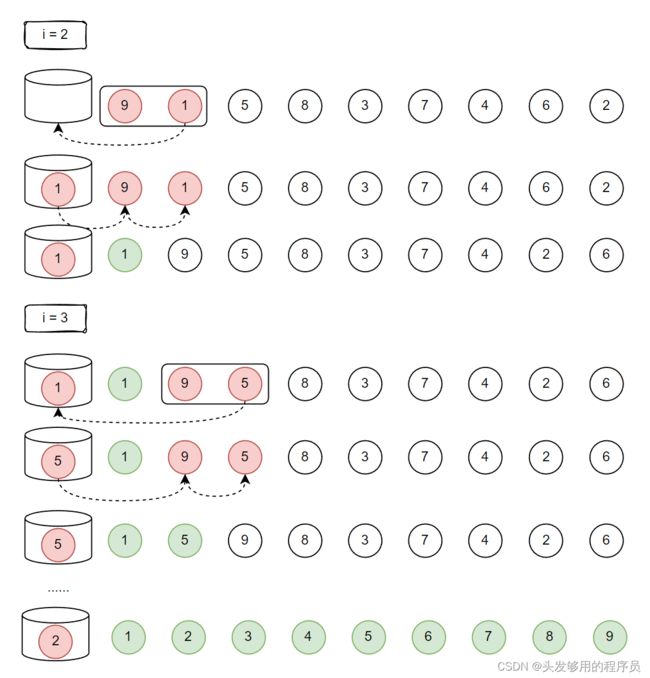
从上图中可以看出，所谓的插入排序，是两两进行比较，若发现顺序相反，则将其放入辅助空间中，然后调整其他元素的位置，找到合适的位置插入，从而完成此次排序。

3.2 插入排序算法总结

与冒泡排序和选择排序算法不同的是，插入排序算法需要一个额外的空间来存储数据，但其性能比前两者要稍微好一些，平均比较和移动的次数约为（n²）/4。

4 希尔排序

希尔排序是D.L.Shell于1959年提出的一种排序算法，希尔排序是第一批突破平方阶时间复杂度的算法之一。

4.1 希尔排序的代码实现

在希尔排序中，需要设置一个增量，然后使其逐渐较小到1，从而顺利完成排序任务。具体实现的代码如下。

#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
void ShellSort(sqList *L)
{
	int i, j, k = 0;
	int increment = L->length;
	do
	{
		increment = increment / 3 + 1;  
		for (i = increment + 1; i <= L->length; i++)
		{
			if (L->r[i] < L->r[i - increment])
			{
				L->r[0] = L->r[i]; 
				for (j = i - increment; j > 0 && L->r[0] < L->r[j]; j -= increment)
					L->r[j + increment] = L->r[j];
				L->r[j + increment] = L->r[0];
			}
		}
	} 
	while (increment > 1);
}
int main()
{
	sqList test = {{0,9,1,5,8,3,7,4,6,2}, 9};
	ShellSort(&test);
	for (int i = 0; i <= test.length; i++)
		printf("%d\t", test.r[i]);
	return 0;
}

从代码中可以看出，希尔排序与插入排序有相似之处，又或者说，希尔排序是一种特殊的插入排序，与插入排序相比，希尔排序是每间隔几个数进行比较大小的，然后每循环一次，间隔减一，直到为0，完成排序。如下图所示：

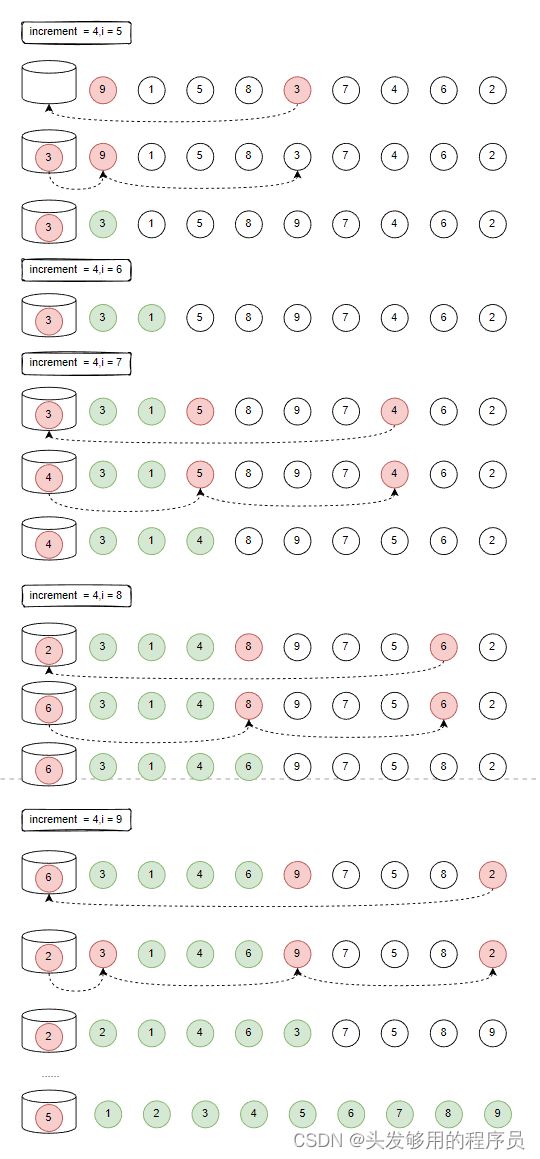
4.2 希尔排序算法总结

同插入排序类似，希尔排序仍然需要一个辅助空间，但其时间复杂度要小一些。有的说法是n^1.3，有的说法是n^1.5。但肯定优于前三种排序算法。

5 堆排序

堆排序是利用推进行排序的一种算法。

堆排序的基本思想是，将待排序的序列构造成一个大顶堆。此时，整个序列的最大值就是堆顶的根节点。将它移走，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次大值。如此反复执行，便能得到一个有序序列了。

5.1 堆简介

堆（数据结构）是具有下列性质的完全二叉树；每个结点的值都大于或者等于其左右孩子结点的值，成为大顶堆；或者每个结点的值都小于或者等于其左右孩子结点的值，称为小顶堆。

从这里也可以看出，推是一种特殊的二叉树。此次排序用的堆是大顶堆。

5.2 堆排序的代码实现

推排序的代码实现如下所示。

#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
//本函数调整L->r[s]的关键字，使L->r[s..m]成为一个大顶堆
void HeapAdjust(sqList *L, int s,int m)
{
	int temp, j;  
	temp = L->r[s];  
	for (j = 2 * s; j <= m; j *= 2)   //沿关键字较大的孩子结点向下筛选
	{
		if (j < m && L->r[j] < L->r[j + 1])   //左孩子的值应小于右孩子
			++j;                              //j的位置变为右孩子，也就是较大值的位置
		if (temp >= L->r[j])                  //当前结点的值应该大于等于孩子结点的值
			break;   
		L->r[s] = L->r[j]; 
		s = j;    
	}
	L->r[s] = temp;  
}
void HeapSort(sqList *L)
{
	int i;
	//构建大顶堆
	for (i = L->length / 2; i > 0; i--)
		HeapAdjust(L, i, L->length);
	//排序
	for (i = L->length; i > 1; i--)
	{
		//将堆顶记录和当前未经排序子序列最后一次记录交换
		swap(L, 1, i);
		//将其重新调整为大顶堆
		HeapAdjust(L, 1 ,i - 1);
	}
}
int main()
{
	sqList test = { {0,50,10,90,30,70,40,80,60,20}, 9 };
	HeapSort(&test);
	for (int i = 0; i <= test.length; i++)
		printf("%d\t", test.r[i]);
	return 0;
}

堆排序的算法有点难理解，大致过程是这样的。

1. 构建大顶堆；
2. 将大顶堆上的根节点（最大值）取出，然后调整大顶堆，这样就可以取出次大值，直到将所有值取出。

下面我们借助图来理解整个堆排序的详细过程。

5.2.1 堆的构建过程

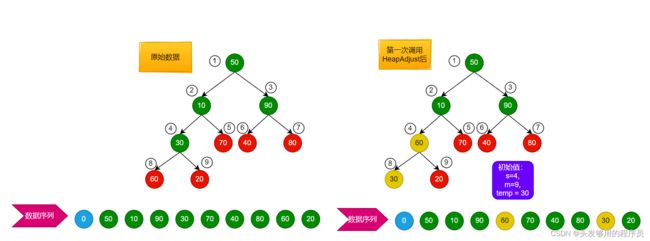
如上图所示，绿色为非叶子结点，也就是调用HeapAdjust的时候，传的第二个参数所指的位置。先调整编号4为根节点的子树。调整过程大概如下：

		if (j < m && L->r[j] < L->r[j + 1])   //左孩子的值应小于右孩子
			++j;                              //j的位置变为右孩子，也就是较大值的位置

以上语句就是检查左子树是否小于右子树的，若小于则指向右孩子结点。显然此时不满足，继续往下运行（也就是说，j指向了较大值所在的孩子结点）；

		if (temp >= L->r[j])                  //当前结点的值应该大于等于孩子结点的值
			break;   

若根节点大于孩子结点，则满足要求，运行结束。此时显然不满足。继续往下运行；

		L->r[s] = L->r[j]; 
		s = j; 

将较大的值赋予根节点（局部）；继续往下运行；j = 16，不满足条件，跳出循环。继续往下运行；

L->r[s] = temp;  //插入新值

也就是L->r[8] = 3；此次调用执行结束。

第二次和第三次调用于此类似，如下所示：

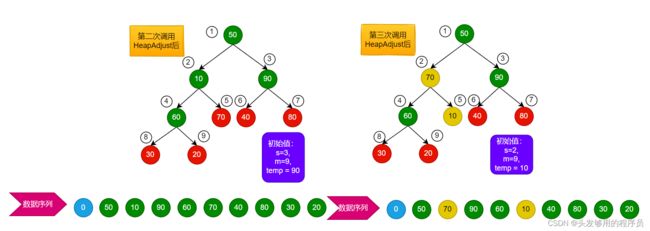
因为3号节点本身就符合要求，因此第二次调用不做改变。
第四次调用稍微麻烦一些：

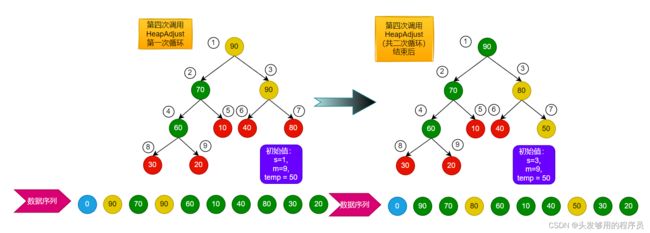
因为这里做了两次循环，且对节点进行了重新赋值。至此，大顶堆构建结束。

5.2.2 堆排序过程

如果将核心思想看懂了，堆的排序过程就变得容易了（图片仅用来说明第一次HeapAdjust函数调用的运行过程，剩下的可自己推理）。如下图所示：

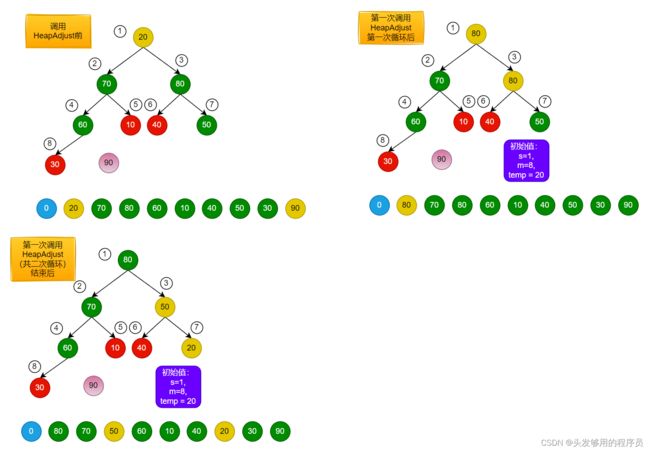
首先，整个大顶堆的根节点肯定是最大值，所以将其放在最后，并对其他部分进行调整（排序），再将值逐个取出，即可完成排序过程。

5.3 堆排序算法总结

总体来说，堆排序的时间复杂度为O(nlongn)。这在性能上显然要远远好过冒泡，选择，插入排序算法了。而且空间复杂度也比较低。

另外，构建堆比较麻烦，因此，它并不合适待排序序列个数比较少的情况。

6 归并排序

前面讲了归并排序，不过堆的构建分身比较麻烦，有没有排序快并且不用这么麻烦的算法呢？归并排序就是一个。

归并排序，就是利用归并的思想实现的排序方法。基本原理是，假设初始记录含有n个记录，则可以看作n个有序的子序列，每个子序列的长度为1，然后两两归并，得到长度为2或者1的子序列；两两归并，如此重复，直至得到一个长度为n的有序序列为止，这种排序方法成为2路归并排序。

有2路归并，自然就有多路归并，本文仅介绍2路归并排序算法。

6.1 归并排序的代码实现

归并排序的实现代码如下。

#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void Merge(int SR[], int TR[], int i, int m, int n)
{
	int j, k, l;
	//将SR中的记录由小到大地并入TR
	for (j = m + 1, k = i; i <= m && j <= n; k++)
	{
		//哪个值小就归并哪个值，直至归并完成
		if (SR[i] < SR[j])
			TR[k] = SR[i++];
		else
			TR[k] = SR[j++];
	}
	//将剩余的SR[i,m]区间的数值复制到TR
	if (i <= m)
	{
		for (l = 0; l <= m - i; l++)
			TR[k + l] = SR[i + l];
	}
	//将剩余的SR[j,n]区间的数值复制到TR
	if (j <= n)
	{
		for (l = 0; l <= n - j; l++)
			TR[k + l] = SR[j + l];
	}

}
void Msort(int SR[], int TR1[], int s, int t)
{
	int m;
	int TR2[MAXSIZE + 1];
	if (s == t)
		TR1[s] = SR[s];
	else
	{
		m = (s + t) / 2;            //将SR[s,t]区间平分为[s,m]和[m+1,t]
		Msort(SR, TR2, s, m);       //递归地将SR[s,m]归并为有序的TR2[s,m]
		Msort(SR, TR2, m + 1, t);   //递归地将SR[m+1，t]归并为有序的TR2[m+1,t]
		Merge(TR2, TR1, s, m, t);   //将TR2[s,m]和TR2[m+1,t]归并到TR1[s,t]
	}
}
void MergeSort(sqList* L)
{
	Msort(L->r, L->r, 0, L->length - 1);
}
int main()
{
	sqList test = { {50,10,90,30,70,40,80,60,20}, 9 };
	MergeSort(&test);
	for (int i = 0; i < test.length; i++)
		printf("%d\t", test.r[i]);
	return 0;
}

归并排序的基本过程如下图所示：

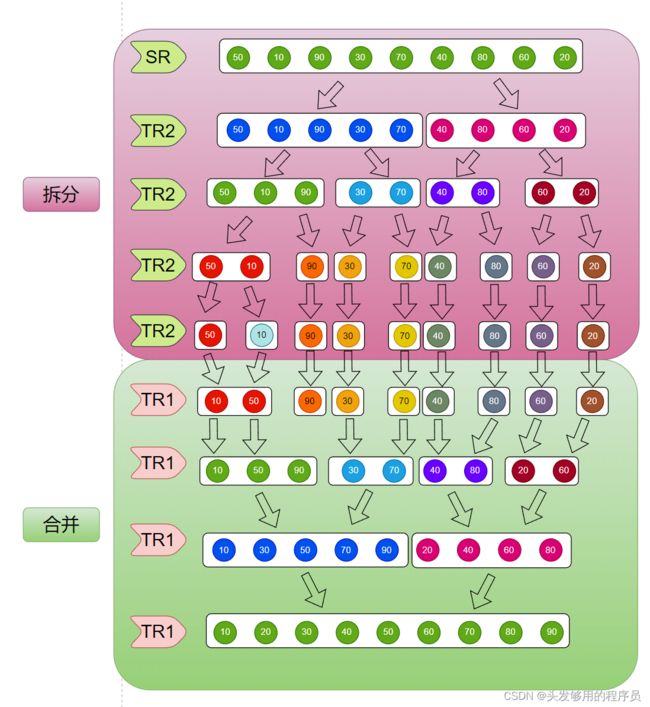
从上图可以发现，归并排序分成两个过程，分别是拆分和合并，在合并的过程中逐步将数据进行排序。
归并排序程序的主体部分如下：

void Msort(int SR[], int TR1[], int s, int t)
{
	int m;
	int TR2[MAXSIZE + 1];
	if (s == t)
		TR1[s] = SR[s];
	else
	{
		m = (s + t) / 2;            //将SR[s,t]区间平分为[s,m]和[m+1,t]
		Msort(SR, TR2, s, m);       //递归地将SR[s,m]归并为有序的TR2[s,m]
		Msort(SR, TR2, m + 1, t);   //递归地将SR[m+1，t]归并为有序的TR2[m+1,t]
		Merge(TR2, TR1, s, m, t);   //将TR2[s,m]和TR2[m+1,t]归并到TR1[s,t]
	}
}

从代码中可以发现，该程序采用了递归，每次都可以将区间分成两半，而Merge函数并未参与到“递”的过程，在此拆分过程中，递归的结束条件是s==t，也就是该区间无法再次拆分的时候，“递”过程结束。

而在“归”的过程中，就有了Merge函数的参与，而“归”是“递”的逆过程，所以此时究竟应该合并哪几个数，在“递”的过程中就已经决定了，只需逆向执行并排序即可。

Merge函数也很好理解，将TR2[s,m]和TR2[m+1,t]归并到TR1[s,t]，哪个值小就先放哪个，并将访问位置后移，如果有一个区间的值提前归并完成，则结束循环，然后将剩下的值复制过去即可。

6.2 归并排序算法总结

归并排序在没有堆排序那么复杂的构建堆的过程前提下，使其拥有了与堆排序相当的时间复杂度。但其需要分配额外空间去存储拆分出来的元素。

归并排序采用将待排序序列进行拆分，再重组的思想简单而高效，这在很多种排序算法中都可以看到。属于典型的空间换时间。

空间换时间是算法里最重要的思想之一。指的是当内存空间充足的时候，为了追求代码的执行速度，可以舍弃对存储空间的要求，从而追求效率。

7 快速排序

快速排序算法最早是由图灵奖获得者Tony Hoare设计出来的，是20世纪最伟大的计算机科学家之一。快速排序在求职面试中是最常考的排序算法之一。

其基本思想是：通过一趟排序将待排记录分割成独立的两部分，其中一部分记录的关键字均比另一部分的关键字小，则可分别对这两部分记录进行排序，以达到整个序列有序的目的。

既然名曰快速排序，在排序速度上至少应该比前面的冒泡，选择和插入排序快，事实的确如此，具体的时间复杂度可以看文章开头的表格。

7.1 快速排序的代码实现

快速排序的代码实现如下。

#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
//交换顺序表L中子表的记录，使枢轴记录到位，并返回其所在位置，
// 此时在它前的数值均小于它
//在它后面的数值均大于它
int Partition(sqList *L, int low, int high)
{
	int pivotkey;
	pivotkey = L->r[low];   //枢轴初始化
	//从两端交替得往中间扫描
	while (low < high)
	{
		while (low < high && L->r[high] >= pivotkey)
			high--;
		swap(L, low, high);    //将比枢轴小的值前移
		while (low < high && L->r[low] <= pivotkey)
			low++;
		swap(L, low, high);    //将比枢轴大的值后移
	}
	return low;
}
void QSort(sqList *L, int low, int hight)
{
	int pivot;
	if (low < hight)
	{
		pivot = Partition(L, low, hight);
		QSort(L, low, pivot - 1);
		QSort(L, pivot + 1, hight);
	}
}
void QuickSort(sqList *L)
{
	QSort(L, 0, L->length - 1);
}
int main()
{
	sqList test = { {9,1,5,8,3,7,4,6,2}, 9 };
	QuickSort(&test);
	for (int i = 0; i < test.length; i++)
		printf("%d\t", test.r[i]);
	return 0;
}

从以上程序中可以看出，在快速排序中，首先要选取枢轴，然后比其小的放在它的前面，比其大的放在后面。让我们分析在Partition函数第一次被调用时的情况。
具体运行情况如下图所示：

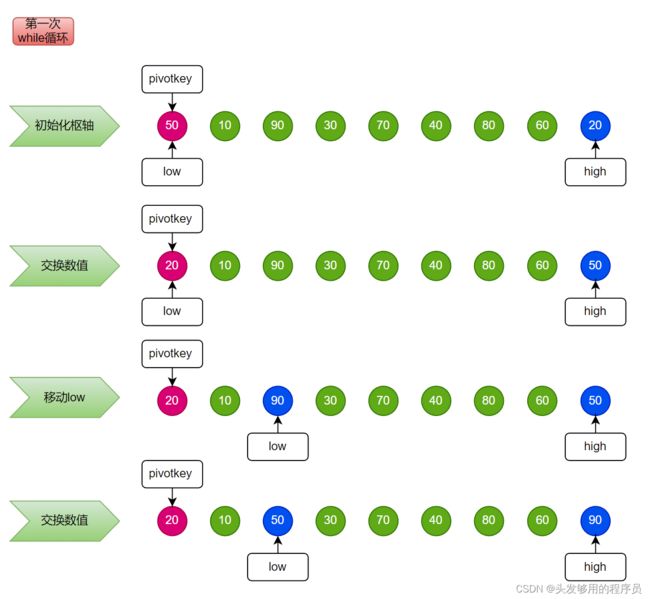
具体执行步骤如下：

• 首先要初始化枢轴，然后将数组其最大和最小位置分别标记为low和high。
• 然后移动high标记，比枢轴大则移动，直至比枢轴小，然后交换low和high的位置。
• 再移动low标记，比枢轴小则移动，直至比枢轴大，然后交换low和high的位置。

从此就可以看到在low位置之前的数值都比low所指的数值小，而high未移动，因而暂时不能说明问题，来看第二次循环。

第二次循环伊始，枢轴放在了low的位置。然后执行相同的流程，发现在low之前的数值都比low所指的数值小，而在high所指及其后面位置的数值，均比low所指的大。

而我们函数返回的数值恰好就是low的数值，也就是整个数组的“分水岭”。然后一直递归，也就是对枢轴的前后两个部分做同样的处理，以此类推，直到low==hight，然后调用返回，返回结束，则排序结束。

7.2 快速排序算法总结

作为最经典，也是面试最常考的排序算法之一，在同样的时间复杂度下，快速排序算法既不需要堆排序那么复杂的堆构建过程，也没有归并排序那么高的空间复杂度。被誉为20世纪十大算法之一，确实有其精妙之处。

8 桶排序

8.1 桶排序的代码实现

桶排序的代码实现如下。

#include 
#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
#define BUCKETNUM 3
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
void BucketSort(sqList *L)
{
	//定义两个变量分别存储原数组中的最大和最小值
	int max = L->r[0];
	int min = L->r[0];
	for (int i = 1; i < L->length; i++)
	{
		if (L->r[i] > max)
			max = L->r[i];
		if (L->r[i] < min)
			min = L->r[i];
	}
	//根据最大最小值以及桶的个数划分桶里的数据
	const int bucket_num = 3;
	//根据大小将所有数共分为10个区间，属于某个区间的就放入某个桶里
	int leng = max - min + 1;   //数组元素的区间长度
	int bucket_size = leng / bucket_num;   //每个桶的数值范围大小
	//创建3个桶
	int bucket[BUCKETNUM][MAXSIZE];
	//记录每个桶中存入数据的数量
	int bucket_sum[BUCKETNUM];
	//桶的初始化
	for (int i = 0; i < BUCKETNUM; i++)
	{
		for(int j = 0; j < MAXSIZE; j++)
			bucket[i][j] = 0;
	}
		
	//计数数组初始化
	for (int i = 0; i < BUCKETNUM; i++)
		bucket_sum[i] = 0;
	//入桶
	for (int i = 0; i < L->length; i++)
	{
		int index = (L->r[i] - min) / bucket_size;
		bucket[index][bucket_sum[index]++] = L->r[i];
		//在元素插入桶的时候使用冒泡排序
		for (int j = bucket_sum[index] - 1; j > 0; j--)
		{
			if (bucket[index][j] < bucket[index][j - 1])
			{
				int temp = bucket[index][j];
				bucket[index][j] = bucket[index][j - 1];
				bucket[index][j - 1] = temp;
			}
		}
	}
	//入桶完毕后，就会得到是个有序的桶，顺序访问桶就能得到有序的数组
	int arr_index = 0;
	for (int i = 0; i < bucket_num; i++)
	{
		for (int j = 0; j < bucket_sum[i]; j++)
			L->r[arr_index++] = bucket[i][j];
	}
}
int main()
{
	sqList test = { {99,11,52,83,36,77,4,63,28}, 9 };
	BucketSort(&test);
	for (int i = 0; i < test.length; i++)
		printf("%d\t", test.r[i]);
	return 0;
}

从以上代码可以看出，整个流程可以分成一下几步：

• 算出待处理序列中的最小值和最大值，并求出取值范围；
• 根据数据的取值范围，求出每个桶可容纳的数值范围大小；
• 创建桶，并初始化；
• 根据每个元素的数值大小分配具体的桶；
• 将元素放入桶中，顺便对该桶中的元素进行排序；
• 将桶内元素取出，即为有序序列。

如下图所示：

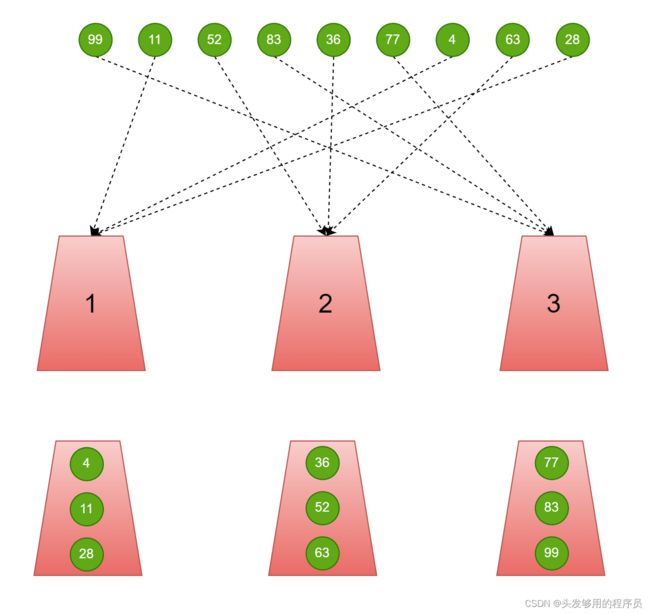
注意每个数值应该放入第几个桶，是根据数值的大小 分布情况来定的。所以一下程序非常重要：

	//根据大小将所有数共分为10个区间，属于某个区间的就放入某个桶里
	int leng = max - min + 1;   //数组元素的区间长度
	int bucket_size = (leng + bucket_num - 1) / bucket_num;   //每个桶的数值范围大小（进一法）

以及：

int index = (L->r[i] - min) / bucket_size;

8.2 桶排序算法总结

桶排序的主要思想是将待排序的数组划分到桶中，至于每个桶中具体的排序算法，可视具体情况而定，桶排序是将数据进行拆分，排序，然后再组合，从而达到了加速的目的。

桶排序的缺点也非常明显，就是对具体数值的大小非常敏感，而当值域很大且分布不均匀时，就会出现桶内数据数量的不均匀，从而导致排序效果变差。比方说下面一组数据：

sqList test = { {99,98,97,8,3,7,4,95,28}, 9 };

在将数据全部放入桶中，出现了下面这种情况：

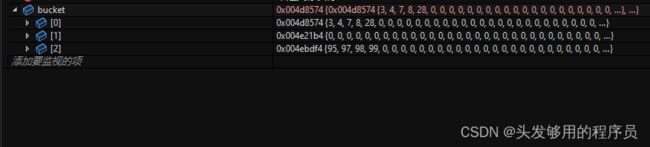
也就是说，出现了桶的分配不均这种情况，甚至出现空桶。

9 基数排序

虽然基数排序被定义为非比较类排序，但其主要思想还是比较，只不过不是直接比较，而是先将序列记录关键字的各个位位值进行比较，先将个位进行比较和排序，然后是十位，直到关键字最大数值的最高位，从而完成排序。

9.1 基数排序的代码实现

基数排序的代码实现如下。

#include 
#include 
#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void RadixSort(sqList* L)
{
	int max = L->r[0];
	for (int i = 1; i < L->length; i++)
	{
		if (L->r[i] > max)
			max = L->r[i];
	}
	//开始从个位一直循环到最大数的最高位
	int flag = 0;
	do {
		//创建十个重复使用的桶
		int buckets[10][MAXSIZE];
		int buckets_size[10];
		for (int i = 0; i < 10; i++)
		{
			buckets_size[i] = 0;
		}
		//入桶
		for (int i = 0; i < L->length; i++)
		{
			int index = (int)(L->r[i] / pow(10, flag)) % 10;
			buckets[index][buckets_size[index]++] = L->r[i];
		}
		//出桶
		int arr_index = 0;
		for (int i = 0; i < 10; i++)
		{
			for (int j = 0; j < buckets_size[i]; j++)
			{
				L->r[arr_index++] = buckets[i][j];
			}
		}
		flag++;
	} while (max /= 10);
}
int main()
{
	sqList test = { {50,99,11,52,83,36,77,4,63,28}, 10 };
	RadixSort(&test);
	for (int i = 0; i < test.length; i++)
		printf("%d\t", test.r[i]);
	return 0;
}

此算法的重点在于确定数值和桶的对应关系，也就是下面这行代码：

int index = (int)(L->r[i] / pow(10, flag)) % 10;

还有外层循环的次数，采用do-while循环，也就是说，至少需要进行一轮排序。
然后就是循环的结束条件while(max /= 10)，从而循环次数就是最大数值的位数。

既然基数排序是从个位开始的，我们先来看看个位的排序，也就是第一次入桶和出桶。

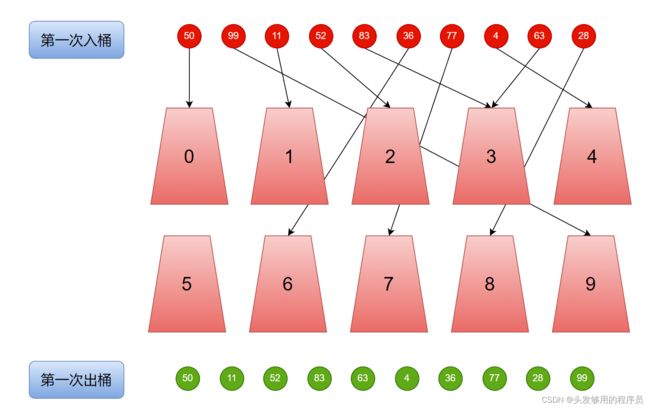
从上图可以看出，第一次入桶，直接根据各个数据的个位数值进行排序，个位数值是几就进几号桶，共有10个桶。

进行完第一轮排序后便到了第二轮排序，让我们看看第二轮排序情况。

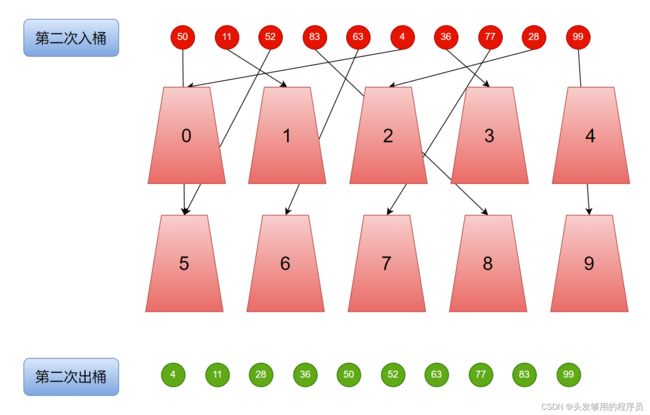
因为最大的数只有两位，因此只需要进行两轮排序即可。从上图可以看出，经过第二轮排序后，整个排序任务已经完成。

9.2 基数排序算法总结

基数排序也是一种比较好理解的排序算法，但需要注意，只能从低位开始比较，若从高位开始比较，到了低位时就会出现错误（很好理解，可以自己试试）。

若本来需要比较的数值是一样的，则不会改变原来的相对顺序，所以基数排序是一种稳定的排序算法。

10 计数排序

计数排序是最好理解的排序算法之一，只需要记录每个数出现的频率，将其放入一个辅助空间中，然后再逐个取出进行排序。

这种排序方法虽然简单直观，也比较高效。但并非所有的情况都适用，该排序算法适用于待排序数据范围比较集中的情况，如果数值范围较大，则需要较大的辅助空间。

10.1 计数排序的代码实现

计数排序的代码实现如下。

#include 
#include 
#include 
#define MAXSIZE 10000
#define TRUE 1
#define FALSE 0
typedef struct
{
	int r[MAXSIZE + 1];
	int length;
}sqList;
void swap(sqList* L, int i, int j)
{
	int temp = L->r[i];
	L->r[i] = L->r[j];
	L->r[j] = temp;
}
void CountSort(sqList* L)
{
	int max = L->r[0];
	int min = L->r[0];
	for (int i = 0; i < L->length; i++)
	{
		if (L->r[i] > max)
			max = L->r[i];
		if (L->r[i] < min)
			min = L->r[i];
	}
	int len = max - min + 1;
	int* arr_temp = (int*)malloc(sizeof(int)*len);
	memset(arr_temp, 0, len*sizeof(int));
	//将索引全部移位到辅助数组中
	for (int i = 0; i < L->length; i++)
		arr_temp[L->r[i] - min]++;
	int index = 0;
	for (int i = 0; i < len; i++)
	{
		while (arr_temp[i] > 0)
		{
			arr_temp[i]--;
			L->r[index++] = i + min;
		}
	}
	free(arr_temp);
}
int main()
{
	sqList test = { {9,1,5,8,3,3,4,6,1,1}, 10};
	CountSort(&test);
	for (int i = 0; i < test.length; i++)
		printf("%d\t", test.r[i]);
	return 0;
}

运行的示意图如下：

从上图可以看出，运行的原理很简单，就是根据待排序序列的数值分布范围分配内存空间，然后对各个数值进行计数，然后取出即可。

10.2 计数排序算法总结

计数排序简单高效，尤其擅长于范围集中，且数据量大的集合。况且由于保存到辅助空间时相同数值按照先后数据一次存入，所以也是稳定的排序算法。

计数排序和桶排序一样，对待排序序列的具体数值非常敏感，若数值范围较大，则需要很大的内存空间来进行辅助排序。

11 后记

千淘万漉虽辛苦，吹尽狂沙始到金。这应该是工程量最大的一篇文章了，从酝酿到发表用了至少一周时间，而在这过程中，也有很多成长和收获。感谢阅读，愿我们一起成长，一起期待美好的未来！