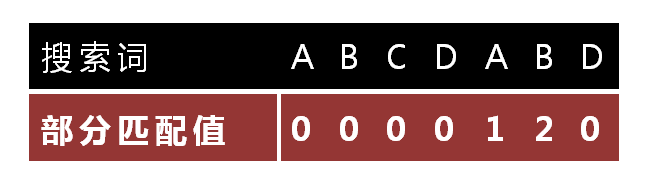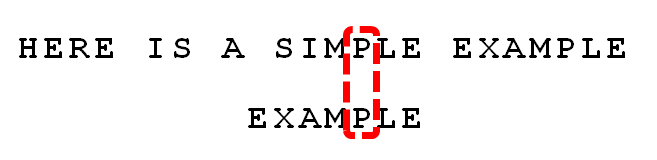字符串匹配算法

1 字符串匹配算法

字符串匹配：输入为原字符串（string）和子串（pattern），要求返回子串在原字符串中首次出现的位置。比如原字符串为“ABCDEFG”，子串为“DEF”，则算法返回3。

常见的算法：

• BF（Brute Force，暴力检索）
• KMP（教科书上最常见算法）
• BM（Boyer Moore）
• RK（Robin-Karp，哈希检索）
• Sunday算法

1.1 暴力检索 BF

首先将匹配串和模式串左对齐，然后从左向右一个一个进行比较，如果不成功则模式串向右移动一个单位。速度最慢。

时间复杂度：O（m*n）

/**
 * 搜索模式字符串P在文本字符串T中第一次出现的位置的蛮力解法
 * 对于文本T中的每个可能的位置，检查P是否匹配，由于文本T的长度为n，模式P的长度为m，
 * 所以T的最后m - 1个位置无需检查，即有n-m+1个可选的位置来比较。
 */
private static int[] F;
public static int bruteForceStringMatch(String T, String P) {
    char[] t = T.toCharArray();
    char[] p = P.toCharArray();
    int n = t.length;
    int m = p.length;

    for(int i = 0; i < n - m + 1; i++) {
        int j = 0;//对p字符串来讲每次都要重新对比
        while(j < m && p[j] == t[i + j]) j++;//匹配则往后
        if(j == m) { return i; }//不匹配则继续进行下一次匹配				
    }	
    return -1;
}

弊端：

BF每次都是重头开始对比，那么如何将前面匹配成功的信息利用起来，极大地减少计算机的处理时间，节省成本？这就出现了KMP算法

1.2 KMP算法

参考文章：字符串匹配的KMP算法 - 阮一峰的网络日志 (ruanyifeng.com)

1.2.1 核心思想

当一趟匹配过程中出现字符不匹配时，不需要回溯主串的指针，而是利用已经得到的“部分匹配”，将模式串尽可能多地向右“滑动”一段距离，然后继续比较。并将部分匹配表这个信息用一个数组存起来

"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，“ABCDAB"之中有两个"AB”，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

KMP算法当模式串内部完全没有重复，那这个算法就可能会退化成遍历

1.2.2 部分匹配表

首先，要了解两个概念：“前缀"和"后缀”。

"前缀"指除了最后一个字符以外，一个字符串的全部头部组合；

"后缀"指除了第一个字符以外，一个字符串的全部尾部组合(注意：都是从前往后排列，对比前后缀是否相等的)

部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度

－　"A"的前缀和后缀都为空集，共有元素的长度为0；

－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

－　“ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A”，长度为1；

－　“ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB”，长度为2；

－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有长度为0。

1.2.3 计算：向后移动的位数

移动位数 = 已匹配的字符数 - 前后缀公共的长度

因为 6 - 2 等于4，所以将搜索词向后移动4位。

因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（“AB”），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

因为空格与A不匹配，继续后移一位。

逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

1.2.4 时间复杂度

• KMP算法需要一个时间和空间开销为O(m)的j预处理（部分匹配函数）过程
• 时间复杂度为O(n+m)

1.2.5 算法实现

• 我们看到如果是在模式串的 j 位 失配， 影响j 指针回溯的位置的其实是第 j −1 位的前后缀匹配值，所以为了编程的方便， 我们不直接使用部分匹配数组数组，而是将部分匹配数组数组向后偏移一位。我们把新得到的这个数组称为next数组。初值赋为-1

• next[j] = k 代表p[j] 之前的模式串子串中，有长度为k 的相同前缀和后缀

• 有了这个next 数组，在KMP匹配中，当模式串中j处的字符失配时，下一步用 next[j]处的字符继续跟文本串匹配，相当于模式串向右移动 j - next[j] 位。

• 重点在如何计算next数组

next数组定义：当主串与模式串的某一位字符不匹配时，模式串要回退的位置。

next[j]=第 j 位字符前面 j-1 位字符组成的子串的前后缀重合字符数 + 1

public class KMP {
    public int kmp(String str, String sub) {
        int i = 0,j = 0;
        int[] next = getNext(sub);
        while (i < str.length() && j < sub.length()){
            if(j == -1 || str.charAt(i) == sub.charAt(j)){//j=-1即第一个元素比较没办法移动，默认往后
                i++;
                j++;
            }else {
                j = next[j];//相当于模式串向右移动 j - next[j] 位。
            }
        }
        if(j == sub.length())//在这里说明已经完全匹配成功，可以直接退出或者进行其他操作
            return i-j;
        else
            return -1;
    }

    public int[] getNext(String sub) {
        int[] next = new int[sub.length()+1];
        int i = 0, j = -1;// i 当前主串正在匹配的字符位置，也是 next 数组的索引
        next[0] = -1;
        while(i<sub.length()){
            if (j==-1 || sub.charAt(i) == sub.charAt(j)){//如果对应位置相等，直接next[j] = next[j-1]+1;
                next[++i] = ++j;
            }else {
                j = next[j];
            }
        }
        return next;
    }
}

可参考文章：https://blog.csdn.net/weixin_43860800/article/details/103695079

可参考视频：https://www.bilibili.com/video/BV16X4y137qw?from=search&seid=17284357682716745667

1.3 BM算法

参考文章：字符串匹配的Boyer-Moore算法 - 阮一峰的网络日志 (ruanyifeng.com)

参考文章：https://www.cnblogs.com/lanxuezaipiao/p/3452579.html

KMP算法并不是效率最高的算法，实际采用并不多。各种文本编辑器的"查找"功能（Ctrl+F），大多采用Boyer-Moore算法。

假定字符串为"HERE IS A SIMPLE EXAMPLE"，搜索词为"EXAMPLE"。

1.3.1 相关概念

1.3.1.1 坏字符：

			"S"与"E"不匹配。这时，**"S"就被称为"坏字符"（bad character），即不匹配的字符。**

坏字符有两种情况：

① "S"不包含在搜索词"EXAMPLE"之中，这意味着可以把搜索词直接移到"S"的后一位

② “P"是"坏字符”。但是，"P"包含在搜索词"EXAMPLE"之中。所以，将搜索词后移两位，两个"P"对齐。

我们由此总结出**“坏字符规则”**：

后移位数 = 坏字符在本次匹配中位于的索引对应位置 - 坏字符在模式串中的相对位置（从0开始编号），如果"坏字符"不包含在搜索词之中，则上一次出现位置为 -1。

以"P"为例，它作为"坏字符"，出现在搜索词的第6位（从0开始编号），在搜索词中的上一次出现位置为4，所以后移 6 - 4 = 2位。

再以前面第二步的"S"为例，它出现在第6位，上一次出现位置是 -1（即未出现），则整个搜索词后移 6 - (-1) = 7位。

1.3.1.2 好后缀

“MPLE"与"MPLE"匹配。我们把这种情况称为"好后缀”，即所有尾部匹配的字符串。注意，“MPLE”、“PLE”、“LE”、"E"都是好后缀。

"好后缀规则"：

后移位数 = 好后缀的位置 - 搜索词中的上一次出现位置

这个规则有三个注意点：

（1）"好后缀"的位置以最后一个字符为准。假定"ABCDEF"的"EF"是好后缀，则它的位置以"F"为准，即5（从0开始计算）。

（2）如果"好后缀"在搜索词中只出现一次，则它的上一次出现位置为 -1。比如，"EF"在"ABCDEF"之中只出现一次，则它的上一次出现位置为-1（即未出现）。

（3）如果"好后缀"有多个，则除了最长的那个"好后缀"，其他"好后缀"的上一次出现位置必须在头部。比如，假定"BABCDAB"的"好后缀"是"DAB"、“AB”、“B”，请问这时"好后缀"的上一次出现位置是什么？回答是，此时采用的好后缀是"B"，它的上一次出现位置是头部，即第0位。这个规则也可以这样表达：如果最长的那个"好后缀"只出现一次，则可以把搜索词改写成如下形式进行位置计算"(DA)BABCDAB"，即虚拟加入最前面的"DA"。

此时，所有的"好后缀"（MPLE、PLE、LE、E）之中，只有"E"在"EXAMPLE"还出现在头部，所以后移 6 - 0 = 6位。

但是根据"坏字符规则"，I是坏字符，此时搜索词应该后移 2 - （-1）= 3 位。

可以看到，"坏字符规则"只能移3位，"好后缀规则"可以移6位。所以，Boyer-Moore算法的基本思想是，每次后移这两个规则之中的较大值。

1.3.2 BM算法全过程

• 首先，"字符串"与"搜索词"头部对齐，从尾部开始比较。

这是一个很聪明的想法，因为如果尾部字符不匹配，那么只要一次比较，就可以知道前7个字符（整体上）肯定不是要找的结果。

• 坏字符移动规则

依然从尾部开始比较，"E"与"E"匹配。

比较前面一位，"LE"与"LE"匹配。

比较前面一位，"PLE"与"PLE"匹配。

• 计算好后缀规则移动的步数、坏字符移动的步数，取其大——6步

根据"坏字符规则"，此时搜索词应该后移 2 - （-1）= 3 位。

所有的"好后缀"（MPLE、PLE、LE、E）之中，只有"E"在"EXAMPLE"还出现在头部，所以后移 6 - 0 = 6位。

继续从尾部开始比较，“P"与"E"不匹配，因此"P"是"坏字符”。根据"坏字符规则"，后移 6 - 4 = 2位。

从尾部开始逐位比较，发现全部匹配，于是搜索结束。如果还要继续查找（即找出全部匹配），则根据"好后缀规则"，后移 6 - 0 = 6位，即头部的"E"移到尾部的"E"的位置。

1.3.3 算法实现

public class BM {
    // BM算法匹配字符串，匹配成功返回P在S中的首字符下标，匹配失败返回-1
    public static int indexOf(String source, String pattern) {
        char[] src = source.toCharArray();
        char[] ptn = pattern.toCharArray();
        int sLen = src.length;
        int pLen = ptn.length;

        // 模式串为空字符串，返回0
        if (pLen == 0) {
            return 0;
        }
        // 主串长度小于模式串长度，返回-1
        if (sLen < pLen) {
            return -1;
        }

        int[] BC = buildBadCharacter(ptn);
        int[] GS = buildGoodSuffix(ptn);

        // 从尾部开始匹配，其中i指向主串，j指向模式串
        for (int i = pLen - 1; i < sLen; ) {
            int j = pLen - 1;
            for (; src[i] == ptn[j]; i--, j--) {
                if (j == 0) {   // 匹配成功返回首字符下标
                    return i;
                }
            }

            // 每次后移“坏字符规则”和“好后缀规则”两者的较大值
            // 注意此时i（坏字符）已经向前移动，所以并非真正意义上的规则
            i += Math.max(BC[src[i]], GS[pLen - 1 - j]);
        }

        return -1;
    }

    // 坏字符规则表
    private static int[] buildBadCharacter(char[] pattern) {
        int pLen = pattern.length;
        final int CHARACTER_SIZE = 256; // 英文字符的种类，2^8
        int[] BC = new int[CHARACTER_SIZE]; // 记录坏字符出现时后移位数

        Arrays.fill(BC, pLen);  // 默认后移整个模式串长度
        for (int i = 0; i < pLen - 1; i++) {
            int ascii = pattern[i];  // 当前字符对应的ASCII值
            BC[ascii] = pLen - 1 - i;   // 对应的后移位数，若重复则以最右边为准
        }

        return BC;
    }

    // 非真正意义上的好字符规则表，后移位数还加上了当前好后缀的最大长度
    private static int[] buildGoodSuffix(char[] pattern) {
        int pLen = pattern.length;
        int[] GS = new int[pLen];   // 记录好后缀出现时后移位数
        int lastPrefixPos = pLen;   // 好后缀的首字符位置

        for (int i = pLen - 1; i >= 0; i--) {
            // 判断当前位置（不含）之后是否是好后缀，空字符也是好后缀
            if (isPrefix(pattern, i + 1)) {
                lastPrefixPos = i + 1;
            }
            // 如果是好后缀，则GS=pLen，否则依次为pLen+1、pLen+2、...
            GS[pLen - 1 - i] = lastPrefixPos - i + pLen - 1;
        }

        // 上面在比较好后缀时，是从模式串的首字符开始的，但实际上好后缀可能出现在模式串中间。
        // 比如模式串EXAMPXA，假设主串指针在比较P时发现是坏字符，那么XA就是好后缀，
        // 虽然它的首字符X与模式串的首字符E并不相等。此时suffixLen=2表示将主串指针后移至模式串末尾，
        // pLen-1-i=4表示真正的好字符规则，同样主串指针后移，使得模式串前面的XA对齐主串的XA
        for (int i = 0; i < pLen - 1; i++) {
            int suffixLen = suffixLength(pattern, i);
            GS[suffixLen] = pLen - 1 - i + suffixLen;
        }

        return GS;
    }

    // 判断是否是好后缀，即模式串begin（含）之后的子串是否匹配模式串的前缀
    private static boolean isPrefix(char[] pattern, int begin) {
        for (int i = begin, j = 0; i < pattern.length; i++, j++) {
            if (pattern[i] != pattern[j]) {
                return false;
            }
        }

        return true;
    }

    // 返回模式串中以pattern[begin]（含）结尾的后缀子串的最大长度
    private static int suffixLength(char[] pattern, int begin) {
        int suffixLen = 0;

        int i = begin;
        int j = pattern.length - 1;
        while (i >= 0 && pattern[i] == pattern[j]) {
            suffixLen++;
            i--;
            j--;
        }

        return suffixLen;
    }
}

1.4 Sunday 算法

Sunday 算法是 Daniel M.Sunday 于1990年提出的字符串模式匹配。其核心思想是：在匹配过程中，模式串发现不匹配时，算法能跳过尽可能多的字符以进行下一步的匹配，从而提高了匹配效率。

1.4.1 匹配过程

从前往后匹配，在匹配失败时关注的是主串中参加匹配的最末位字符的下一位字符。

• 如果该字符没有在模式串中出现则直接跳过，即移动位数 = 模式串长度 + 1；
• 否则，其移动位数 = 模式串长度 - 该字符最右出现的位置(以0开始) = 模式串中该字符最右出现的位置到尾部的距离 + 1。

1.4.2 案例

一般来讲，字符串匹配算法第一步，都是把目标串和模式串对齐。不管是KMP，BM，SUNDAY都是这样。

而对于SUNDAY算法，我们从头部开始比较，一旦发现不匹配，直接找到主串中位于模式串后面的第一个字符，即下面绿色的 “s”。（这里说明一下，为什么是找模式串后面的第一个字符。在把模式串和目标串对齐后，如果发现不匹配，那肯定需要移动模式串。问题是需要移动多少步。各字符串匹配算法之间的差别也来自于这个地方，对于KMP，是建立部分匹配表来计算。BM，是反向比较计算移动量。对于SUNDAY，就是找到模式串后的第一个字符。因为，无论模式串移动多少步，模式串后的第一个字符都要参与下一次比较，也就是这里的 “s”）

找到了模式串后的第一个字符 “s”，接下来该怎么做？我们需要查看模式串中是否包含这个元素，如果不包含那就可以跳过一大片，从该字符的下一个字符开始比较。

因为仍然不匹配（空格和l），我们继续重复上面的过程。找到模式串的下一个元素：t

现在有意思了，我们发现 t 被包含于模式串中，并且 t 出现在模式串倒数第3个。所以我们把模式串向前移动3个单位：

匹配成功!

这个过程里我们做了一些什么：

• 对齐目标串和模式串，从前向后匹配
• 关注主串中位于模式串后面的第一个元素（核心）
• 如果关注的字符没有在子串中出现则直接跳过
• 否则开始移动模式串，移动位数 = 子串长度 - 该字符最右出现的位置(以0开始)

参考文章：https://www.cnblogs.com/r1-12king/p/13293426.html

1.4.3 缺点：

主串：baaaabaaaabaaaabaaaa
子串：aaaaa
这个时候，效率瞬间变成了O(m*n)
Sunday算法的移动是取决于子串的，这一点跟BM算法没什么区别，当这个子串重复很多的时候，就会非常糟糕了。大家知道这一点，有所取舍就好

时间复杂度：

KMP O(m+n)
BM O(m/n) - O(m*n)
Sunday O(m/n) - O(m*n)
实际使用中 Sunday算法比BM算法略优

1.4.4 实现

public class test {
    public static void main(String[] args) {
        String s="abcdebcdbcdegbcde";
        String p="bcdeg";
        Sunday(s, p);

    }
    //注意每次都是从后向前
    public static int contains(char[] str,char ch){
        for(int i=str.length-1;i>=0;i--){
            if(str[i]==ch){
                return i;
            }
        }
        return -1;
    }
    public int Sunday(String s,String p){
        char[] sarray = s.toCharArray();
        char[] parray = p.toCharArray();
        int slen=s.length();
        int plen=p.length();
        int i=0,j=0;
        while(i<=slen-plen+j){//这句话控制索引i,j的范围
            if(sarray[i]!=parray[j]){//假如主串的sarry[i]与模式串的parray[j]不相等
                if(i==slen-plen+j){//
                    return -1;//假如主串的sarry[i]与模式串的parray[j]不相等,并且i=slen-plen+j,说明这已经
                    //是在和主串中最后可能相等的字符段比较了,并且不相等,说明后面就再也没有相等的了,所以
                    //跳出循环,结束匹配
                }
                //假如是主串的中间字段与模式串匹配，且结果不匹配
                //则就从模式串的最后面开始,从后向前遍历,找出模式串的后一位在对应的母串的字符是否在子串中存在
                int pos=contains(parray, sarray[i+plen-j]);
                if(pos==-1){//表示不存在
                    i=i+plen+1-j;
                    j=0;
                }else{
                    i=i+plen-pos-j;
                    j=0;
                }
            }else{//假如主串的sarry[i]与模式串的parray[j]相等,则继续下面的操作
                if(j==plen-1){//判断模式串的索引j是不是已经到达模式串的最后位置，
                    //j==plen-1证明在主串中已经找到一个模式串的位置,
                    //且目前主串尾部的索引为i,主串首部的索引为i-j,打印模式串匹配的第一个位置
                    //System.out.println("the start pos is "+(i-j)+" the end pos is "+i);
                    return i-j;
                    //然后主串右移一个位置,再和模式串的首字符比较,从而寻找下一个匹配的位置
                    i=i-j+1;
                    j=0;
                }else{
                    //假如模式串的索引j!=plen-1,说明模式串还没有匹配完,则i++,j++继续匹配,
                    i++;
                    j++;
                }
            }
        }
    }
}

• 实例：LeetCode.28 - 实现strStr()