小白学Pytorch 系列--Torch API（2）

小白学Pytorch 系列–Torch API（2）

Generators

torch.Generator

创建并返回一个生成器对象，该对象管理生成伪随机数的算法的状态。在许多就地随机抽样函数中用作关键字参数。

g_cpu = torch.Generator()
g_cpu.get_state()

g_cpu = torch.Generator()
g_cpu.initial_seed()

g_cpu = torch.Generator()
g_cpu.manual_seed(2147483647)

Random sampling

TORCH.SEED

将用于生成随机数的种子设置为非确定性随机数。返回用于为RNG设定种子的64位数字。

TORCH.MANUAL_SEED

设置生成随机数的种子。返回torch.Generator对象。

TORCH.INITIAL_SEED

返回用于生成Python长随机数的初始种子。

TORCH.GET_RNG_STATE

以torch.ByteTensor的形式返回随机数生成器状态。

TORCH.SET_RNG_STATE

设置随机数生成器状态。

TORCH.BERNOULLI

从伯努利分布中绘制二进制随机数(0或1)。
输入张量应该是包含用于绘制二进制随机数的概率的张量。因此，输入中的所有值都必须在该范围内:$0<=inpu{t}_i<=1$

返回的张量只有0或1的值，并且与输入的形状相同。
输出可以是整型dtype，但输入必须是浮点型dtype。

>>> a = torch.empty(3, 3).uniform_(0, 1)  # generate a uniform random matrix with range [0, 1]
>>> a
tensor([[ 0.1737,  0.0950,  0.3609],
        [ 0.7148,  0.0289,  0.2676],
        [ 0.9456,  0.8937,  0.7202]])
>>> torch.bernoulli(a)
tensor([[ 1.,  0.,  0.],
        [ 0.,  0.,  0.],
        [ 1.,  1.,  1.]])

>>> a = torch.ones(3, 3) # probability of drawing "1" is 1
>>> torch.bernoulli(a)
tensor([[ 1.,  1.,  1.],
        [ 1.,  1.,  1.],
        [ 1.,  1.,  1.]])
>>> a = torch.zeros(3, 3) # probability of drawing "1" is 0
>>> torch.bernoulli(a)
tensor([[ 0.,  0.,  0.],
        [ 0.,  0.,  0.],
        [ 0.,  0.,  0.]])

TORCH.MULTINOMIAL

以输入的张量作为权重进行多分布采样

输入行不需要求和为1（在这种情况下，我们使用值作为权重），但必须是非负的、有限的且具有非零和。

根据每个索引的采样时间从左到右排序（第一个样本放在第一列）。
对input的每一行进行num_samples次取值，输出为每次取值的索引。
input每一行中的元素是该索引被采样的权重。如果元素为0，那么其他位置被采样完之前，这个位置都不会被采样。
replacement=False为不放回采样，True为有放回采样。

>>> weights = torch.tensor([0, 10, 3, 0], dtype=torch.float) # create a tensor of weights
>>> torch.multinomial(weights, 2)
tensor([1, 2])
>>> torch.multinomial(weights, 4) # ERROR!
RuntimeError: invalid argument 2: invalid multinomial distribution (with replacement=False,
not enough non-negative category to sample) at ../aten/src/TH/generic/THTensorRandom.cpp:320
>>> torch.multinomial(weights, 4, replacement=True)
tensor([ 2,  1,  1,  1])

TORCH.NORMAL

该函数返回从单独的正态分布中提取的随机数的张量，该正态分布的均值是mean，标准差是std。

torch.normal(mean=torch.arange(1., 11.), std=torch.arange(1, 0, -0.1))
torch.normal(mean=0.5, std=torch.arange(1., 6.))
torch.normal(mean=torch.arange(1., 6.))
torch.normal(2, 3, size=(1, 4))

TORCH.POISSON

返回与输入相同大小的张量，其中每个元素从泊松分布采样。，

rates = torch.rand(4, 4) * 5  # rate parameter between 0 and 5
torch.poisson(rates)

TORCH.RAND

返回一个张量，由区间[0,1]上均匀分布的随机数填充。
张量的形状由变量参数size定义。

torch.rand(4)
torch.rand(2, 3)

TORCH.RAND_LIKE

返回与输入大小相同的张量，该张量由区间[0,1）上均匀分布的随机数填充。
torch.rand_like(input)等效于torch.rand(input.size()，dtype=input.dtype，layout=input.layout，device=input.device)。

TORCH.RANDINT

返回一个张量，该张量由在低（含）和高（不含）之间均匀生成的随机整数填充。

张量的形状由可变参数大小定义。

torch.randint(3, 5, (3,))
torch.randint(10, (2, 2))
torch.randint(3, 10, (2, 2))

TORCH.RANDINT_LIKE

返回一个与张量输入形状相同的张量，该张量填充有在低（含）和高（不含）之间均匀生成的随机整数。

TORCH.RANDN

返回由平均值为0和方差为1的正态分布（也称为标准正态分布）中的随机数填充的张量。

torch.randperm(4)

TORCH.RANDN_LIKE

返回一个与输入大小相同的张量，该张量由均值为0、方差为1的正态分布中的随机数填充。torch.randn_like(input)等同于torch.randn(input.size()，dtype=input.dtype，layout=input.layout，device=input.device)。

TORCH.RANDPERM

返回从0到n-1的整数的随机排列。

torch.randperm(4)

In-place random sampling

在张量上还定义了更多的就地随机抽样函数。点击查看他们的文档

• torch.Tensor.bernoulli_()-torch.bernoulli()的原地版本
  从伯努利分布中提取二进制随机数（0或1），输入张量应为包含用于绘制二进制随机数的概率的张量。因此，输入中的所有值都必须在以下范围内(0,1)。
  

>>> a = torch.empty(3, 3).uniform_(0, 1)  # generate a uniform random matrix with range [0, 1]
>>> a
tensor([[ 0.1737,  0.0950,  0.3609],
        [ 0.7148,  0.0289,  0.2676],
        [ 0.9456,  0.8937,  0.7202]])
>>> torch.bernoulli(a)
tensor([[ 1.,  0.,  0.],
        [ 0.,  0.,  0.],
        [ 1.,  1.,  1.]])

>>> a = torch.ones(3, 3) # probability of drawing "1" is 1
>>> torch.bernoulli(a)
tensor([[ 1.,  1.,  1.],
        [ 1.,  1.,  1.],
        [ 1.,  1.,  1.]])
>>> a = torch.zeros(3, 3) # probability of drawing "1" is 0
>>> torch.bernoulli(a)
tensor([[ 0.,  0.,  0.],
        [ 0.,  0.,  0.],
        [ 0.,  0.,  0.]])

• torch.Tensor.cauchy_()-从柯西分布中得到的数
  

>>> a = torch.ones(3, 3)
>>> torch.Tensor.cauchy_(a)
tensor([[-4.5374, 0.3726, 0.4947],
[ 0.4111, 0.9167, 0.7214],
[ 1.0533, -9.2247, 0.7620]])

• torch.Tensor.exponential_()-从指数分布中抽取的数字

a = torch.ones(3, 3)
c = torch.Tensor.exponential_(a)

tensor([[0.3893, 0.0695, 0.6871],
        [0.0591, 0.3779, 0.9806],
        [0.2019, 0.2062, 0.9049]])

• torch.Tensor.geometric_() - 从几何分布中绘制的元素

a = torch.ones(3, 3)
c = torch.Tensor.geometric_(a)

tensor([[  2.8285,   1.6213,   0.6245],
        [  3.0095, 153.3951,   0.2924],
        [  2.7817,   3.9648,   0.5211]])

• torch.Tensor.log_normal_() - 样本来自对数正态分布

a = torch.ones(3, 3)
c = torch.Tensor.log_normal_(a)

tensor([[  2.8285,   1.6213,   0.6245],
        [  3.0095, 153.3951,   0.2924],
        [  2.7817,   3.9648,   0.5211]])

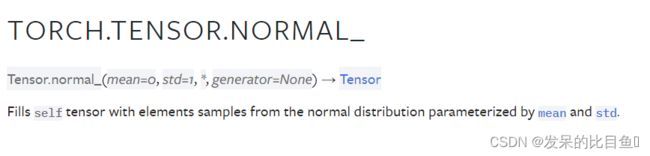
• torch.Tensor.normal_() - torch.normal()的原地版本

a = torch.ones(3, 3)
c = torch.Tensor.normal_(a)

tensor([[  2.8285,   1.6213,   0.6245],
        [  3.0095, 153.3951,   0.2924],
        [  2.7817,   3.9648,   0.5211]])

• torch.Tensor.random_() - 从离散均匀分布中抽样的数

用从 [from, to - 1] 上的离散均匀分布采样的数字填充自张量。如果未指定，则值通常仅受 self 张量数据类型的限制。但是，对于浮点类型，如果未指定，范围将为 [0, 2^mantissa] 以确保每个值都是可表示的。例如 torch.tensor(1, dtype=torch.double).random () 将在 [0, 2^53] 内统一。

a = torch.ones(3, 3)
c = torch.Tensor.random_(a)

• torch.Tensor.uniform_() - 连续均匀分布的抽样数

a = torch.ones(3, 3)
c = torch.Tensor.uniform_(a)
tensor([[0.8895, 0.0307, 0.2593],
        [0.3435, 0.7643, 0.0648],
        [0.9184, 0.4584, 0.8865]])

Quasi-random sampling

quasirandom.SobolEngine

torch.quasrandom.sobolengine是一个用于生成(打乱的)Sobol序列的引擎。Sobol序列是低差异准随机序列的一个例子。
这个Sobol序列引擎的实现能够对最大维数为21201的序列进行采样。它使用来自https://web.maths.unsw.edu.au/~fkuo/sobol/使用搜索标准D(6)获得，直到维度21201。这是作者推荐的选择。

• draw函数从SOBOL序列中绘制n个点的序列。请注意，样品取决于先前的样品。结果的大小是(n,dimension).

soboleng = torch.quasirandom.SobolEngine(dimension=5)
b = soboleng.draw(3)
tensor([[0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
        [0.5000, 0.5000, 0.5000, 0.5000, 0.5000],
        [0.7500, 0.2500, 0.2500, 0.2500, 0.7500]])