小白学Pytorch系列--Torch API (6)

小白学Pytorch系列-- Torch API (6)

Reduction Ops

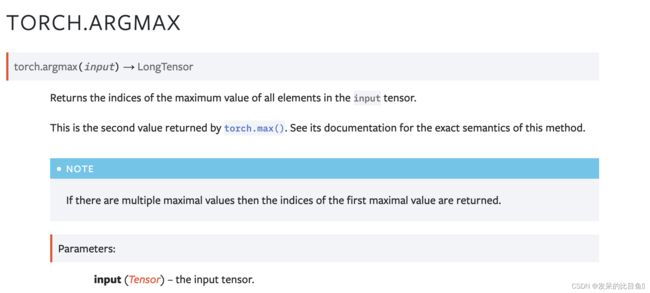
argmax

返回输入张量中所有元素的最大值的索引。

>>> a = torch.randn(4, 4)
>>> a
tensor([[ 1.3398,  0.2663, -0.2686,  0.2450],
        [-0.7401, -0.8805, -0.3402, -1.1936],
        [ 0.4907, -1.3948, -1.0691, -0.3132],
        [-1.6092,  0.5419, -0.2993,  0.3195]])
>>> torch.argmax(a)
tensor(0)

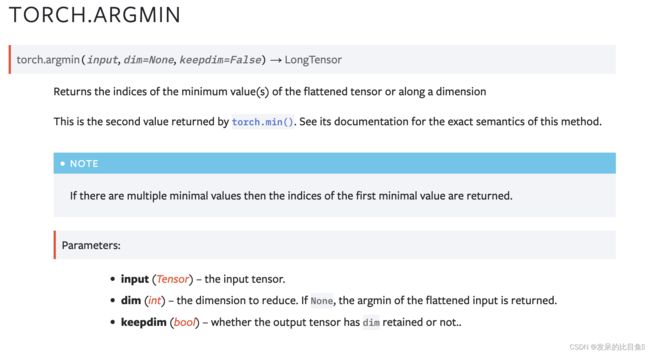
argmin

>>> a = torch.randn(4, 4)
>>> a
tensor([[ 0.1139,  0.2254, -0.1381,  0.3687],
        [ 1.0100, -1.1975, -0.0102, -0.4732],
        [-0.9240,  0.1207, -0.7506, -1.0213],
        [ 1.7809, -1.2960,  0.9384,  0.1438]])
>>> torch.argmin(a)
tensor(13)
>>> torch.argmin(a, dim=1)
tensor([ 2,  1,  3,  1])
>>> torch.argmin(a, dim=1, keepdim=True)
tensor([[2],
        [1],
        [3],
        [1]])

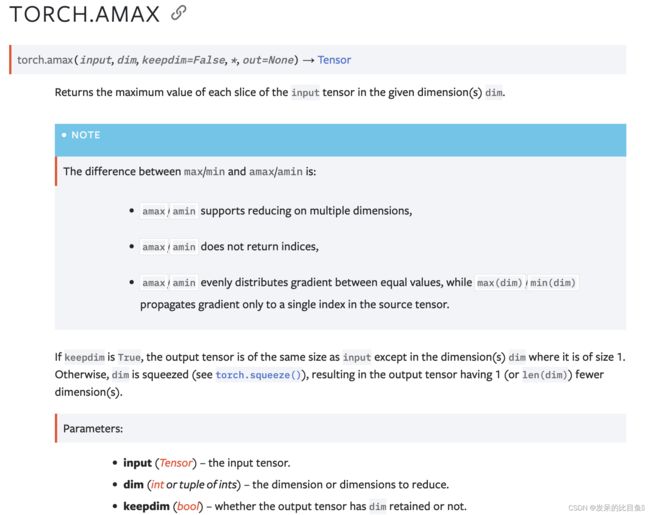
amax

返回给定维度中输入张量的每个切片的最大值

>>> a = torch.randn(4, 4)
>>> a
tensor([[ 0.8177,  1.4878, -0.2491,  0.9130],
        [-0.7158,  1.1775,  2.0992,  0.4817],
        [-0.0053,  0.0164, -1.3738, -0.0507],
        [ 1.9700,  1.1106, -1.0318, -1.0816]])
>>> torch.amax(a, 1)
tensor([1.4878, 2.0992, 0.0164, 1.9700])

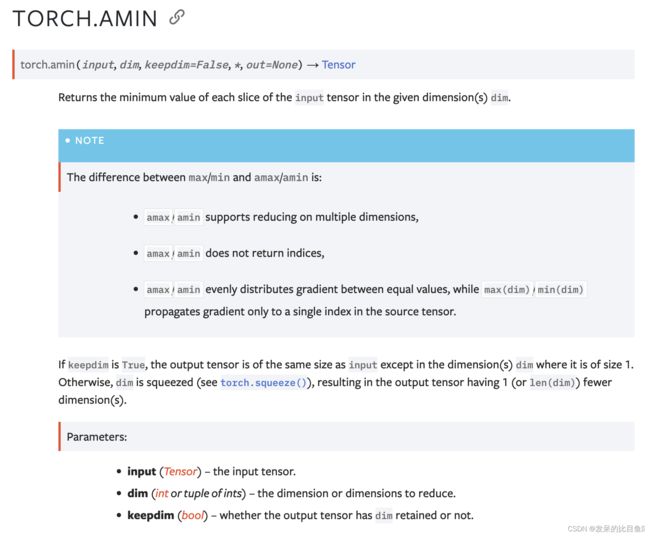
amin

返回给定维度 dim 中输入张量的每个切片的最小值。

>>> a = torch.randn(4, 4)
>>> a
tensor([[ 0.6451, -0.4866,  0.2987, -1.3312],
        [-0.5744,  1.2980,  1.8397, -0.2713],
        [ 0.9128,  0.9214, -1.7268, -0.2995],
        [ 0.9023,  0.4853,  0.9075, -1.6165]])
>>> torch.amin(a, 1)
tensor([-1.3312, -0.5744, -1.7268, -1.6165])

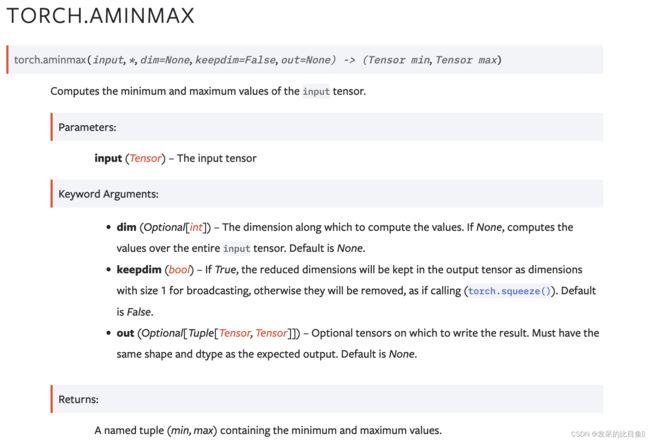
aminmax

计算输入张量的最小值和最大值。

>>> torch.aminmax(torch.tensor([1, -3, 5]))
torch.return_types.aminmax(
min=tensor(-3),
max=tensor(5))

>>> # aminmax propagates NaNs
>>> torch.aminmax(torch.tensor([1, -3, 5, torch.nan]))
torch.return_types.aminmax(
min=tensor(nan),
max=tensor(nan))

>>> t = torch.arange(10).view(2, 5)
>>> t
tensor([[0, 1, 2, 3, 4],
        [5, 6, 7, 8, 9]])
>>> t.aminmax(dim=0, keepdim=True)
torch.return_types.aminmax(
min=tensor([[0, 1, 2, 3, 4]]),
max=tensor([[5, 6, 7, 8, 9]]))

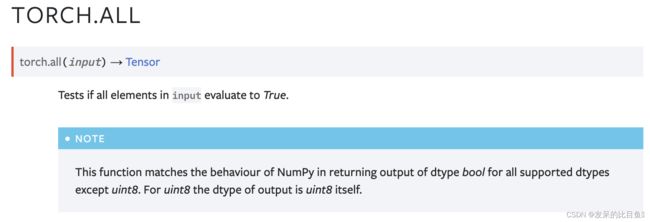
all

测试输入中的所有元素是否都为 True。

>>> a = torch.rand(1, 2).bool()
>>> a
tensor([[False, True]], dtype=torch.bool)
>>> torch.all(a)
tensor(False, dtype=torch.bool)
>>> a = torch.arange(0, 3)
>>> a
tensor([0, 1, 2])
>>> torch.all(a)
tensor(False)

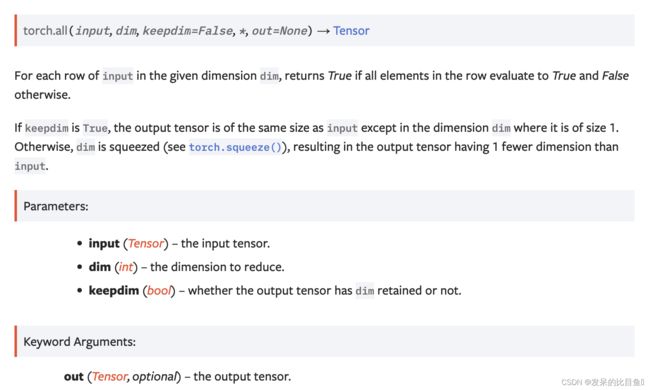
对于给定维度 dim 中的每一行输入，如果该行中的所有元素都评估为 True 则返回 True，否则返回 False。

>>> a = torch.rand(4, 2).bool()
>>> a
tensor([[True, True],
        [True, False],
        [True, True],
        [True, True]], dtype=torch.bool)
>>> torch.all(a, dim=1)
tensor([ True, False,  True,  True], dtype=torch.bool)
>>> torch.all(a, dim=0)
tensor([ True, False], dtype=torch.bool)

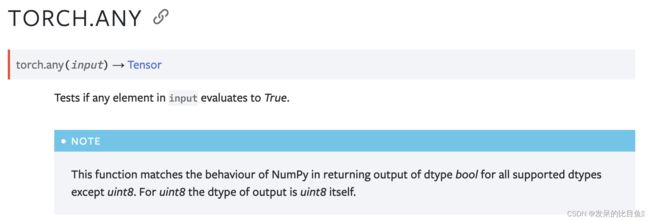
any

测试输入中的任何元素是否计算为 True。

>>> a = torch.rand(1, 2).bool()
>>> a
tensor([[False, True]], dtype=torch.bool)
>>> torch.any(a)
tensor(True, dtype=torch.bool)
>>> a = torch.arange(0, 3)
>>> a
tensor([0, 1, 2])
>>> torch.any(a)
tensor(True)

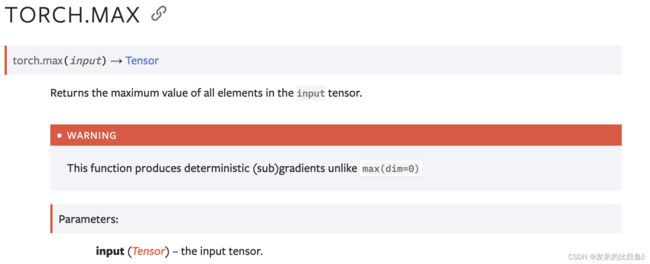
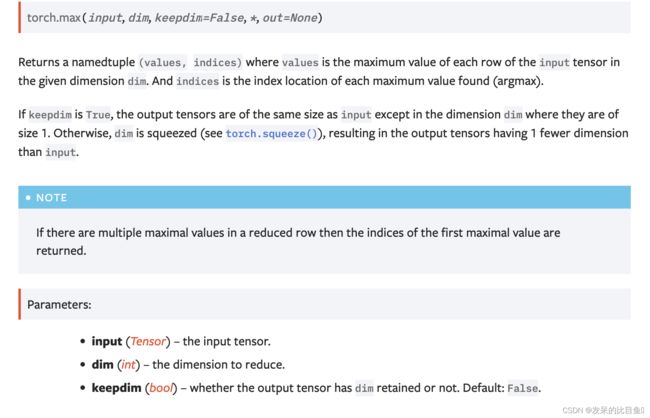
max

返回输入张量中所有元素的最大值。

>>> a = torch.randn(1, 3)
>>> a
tensor([[ 0.6763,  0.7445, -2.2369]])
>>> torch.max(a)
tensor(0.7445)

>>> a = torch.randn(4, 4)
>>> a
tensor([[-1.2360, -0.2942, -0.1222,  0.8475],
        [ 1.1949, -1.1127, -2.2379, -0.6702],
        [ 1.5717, -0.9207,  0.1297, -1.8768],
        [-0.6172,  1.0036, -0.6060, -0.2432]])
>>> torch.max(a, 1)
torch.return_types.max(values=tensor([0.8475, 1.1949, 1.5717, 1.0036]), indices=tensor([3, 0, 0, 1]))

min

返回输入张量中所有元素的最小值。

>>> a = torch.randn(1, 3)
>>> a
tensor([[ 0.6750,  1.0857,  1.7197]])
>>> torch.min(a)
tensor(0.6750)

>>> a = torch.randn(4, 4)
>>> a
tensor([[-0.6248,  1.1334, -1.1899, -0.2803],
        [-1.4644, -0.2635, -0.3651,  0.6134],
        [ 0.2457,  0.0384,  1.0128,  0.7015],
        [-0.1153,  2.9849,  2.1458,  0.5788]])
>>> torch.min(a, 1)
torch.return_types.min(values=tensor([-1.1899, -1.4644,  0.0384, -0.1153]), indices=tensor([2, 0, 1, 0]))

dist

返回（输入 - 其他）的 p-范数

input 和 other 的形状必须是可广播的。

>>> x = torch.randn(4)
>>> x
tensor([-1.5393, -0.8675,  0.5916,  1.6321])
>>> y = torch.randn(4)
>>> y
tensor([ 0.0967, -1.0511,  0.6295,  0.8360])
>>> torch.dist(x, y, 3.5)
tensor(1.6727)
>>> torch.dist(x, y, 3)
tensor(1.6973)
>>> torch.dist(x, y, 0)
tensor(4.)
>>> torch.dist(x, y, 1)
tensor(2.6537)

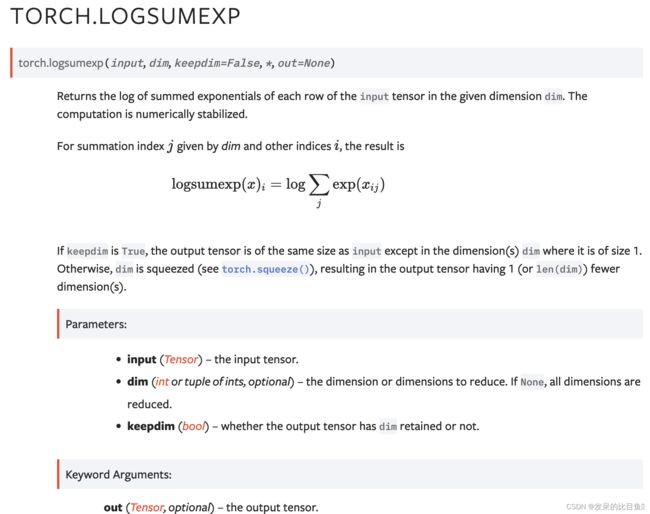
logsumexp

返回给定维度 dim 中输入张量的每一行的指数求和的对数。 计算在数值上是稳定的。

>>> a = torch.randn(3, 3)
>>> torch.logsumexp(a, 1)
tensor([1.4907, 1.0593, 1.5696])
>>> torch.dist(torch.logsumexp(a, 1), torch.log(torch.sum(torch.exp(a), 1)))
tensor(1.6859e-07)

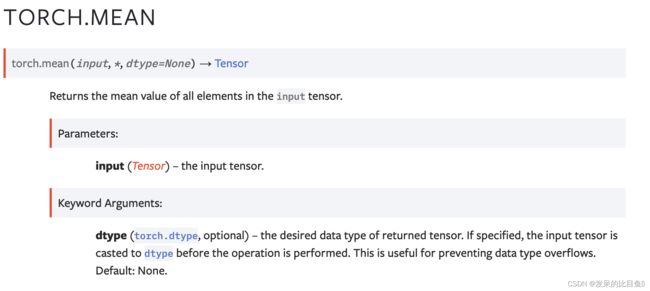
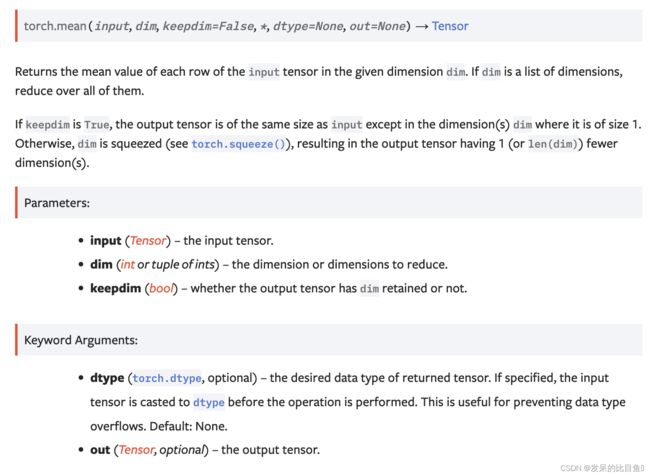
mean

返回输入张量中所有元素的平均值。

>>> a = torch.randn(1, 3)
>>> a
tensor([[ 0.2294, -0.5481,  1.3288]])
>>> torch.mean(a)
tensor(0.3367)

>>> a = torch.randn(4, 4)
>>> a
tensor([[-0.3841,  0.6320,  0.4254, -0.7384],
        [-0.9644,  1.0131, -0.6549, -1.4279],
        [-0.2951, -1.3350, -0.7694,  0.5600],
        [ 1.0842, -0.9580,  0.3623,  0.2343]])
>>> torch.mean(a, 1)
tensor([-0.0163, -0.5085, -0.4599,  0.1807])
>>> torch.mean(a, 1, True)
tensor([[-0.0163],
        [-0.5085],
        [-0.4599],
        [ 0.1807]])

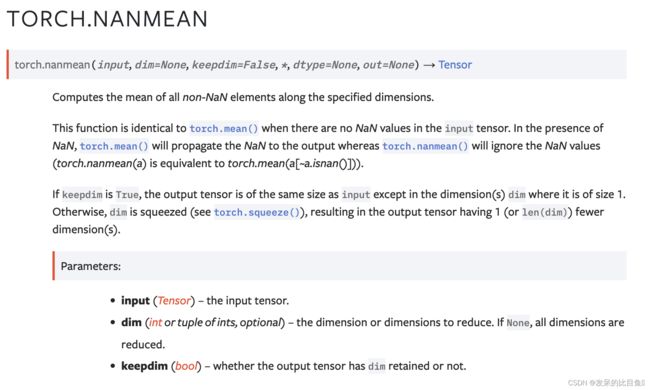
nanmean

计算指定维度上所有非 NaN 元素的平均值。

>>> x = torch.tensor([[torch.nan, 1, 2], [1, 2, 3]])
>>> x.mean()
tensor(nan)
>>> x.nanmean()
tensor(1.8000)
>>> x.mean(dim=0)
tensor([   nan, 1.5000, 2.5000])
>>> x.nanmean(dim=0)
tensor([1.0000, 1.5000, 2.5000])

# If all elements in the reduced dimensions are NaN then the result is NaN
>>> torch.tensor([torch.nan]).nanmean()
tensor(nan)

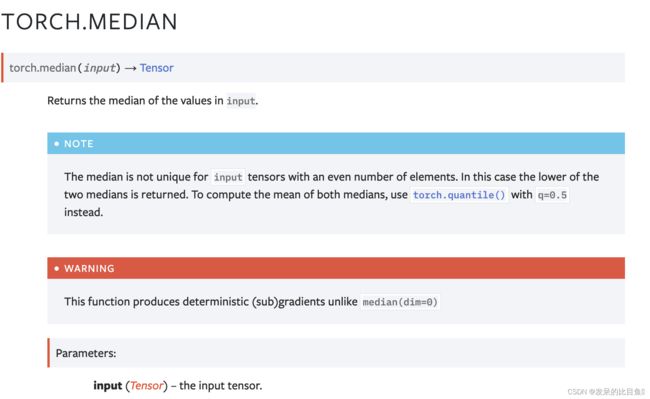
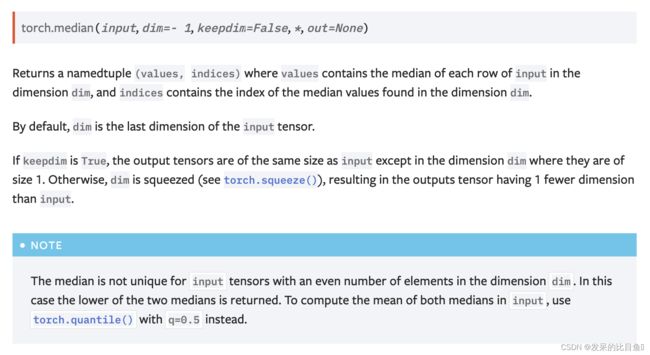
median

返回输入值的中值。

>>> a = torch.randn(1, 3)
>>> a
tensor([[ 1.5219, -1.5212,  0.2202]])
>>> torch.median(a)
tensor(0.2202)

>>> a = torch.randn(4, 5)
>>> a
tensor([[ 0.2505, -0.3982, -0.9948,  0.3518, -1.3131],
        [ 0.3180, -0.6993,  1.0436,  0.0438,  0.2270],
        [-0.2751,  0.7303,  0.2192,  0.3321,  0.2488],
        [ 1.0778, -1.9510,  0.7048,  0.4742, -0.7125]])
>>> torch.median(a, 1)
torch.return_types.median(values=tensor([-0.3982,  0.2270,  0.2488,  0.4742]), indices=tensor([1, 4, 4, 3]))

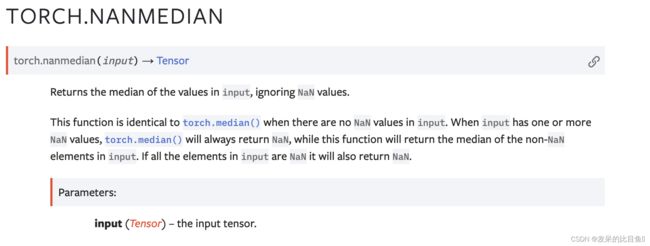
nanmedian

返回输入值的中值，忽略 NaN 值。

>>> a = torch.tensor([1, float('nan'), 3, 2])
>>> a.median()
tensor(nan)
>>> a.nanmedian()
tensor(2.)

>>> a = torch.tensor([[2, 3, 1], [float('nan'), 1, float('nan')]])
>>> a
tensor([[2., 3., 1.],
        [nan, 1., nan]])
>>> a.median(0)
torch.return_types.median(values=tensor([nan, 1., nan]), indices=tensor([1, 1, 1]))
>>> a.nanmedian(0)
torch.return_types.nanmedian(values=tensor([2., 1., 1.]), indices=tensor([0, 1, 0]))

mode

返回一个 namedtuple (values, indices)，其中 values 是给定维度 dim 中输入张量的每一行的模式值，即该行中最常出现的值，indices 是找到的每个模式值的索引位置。

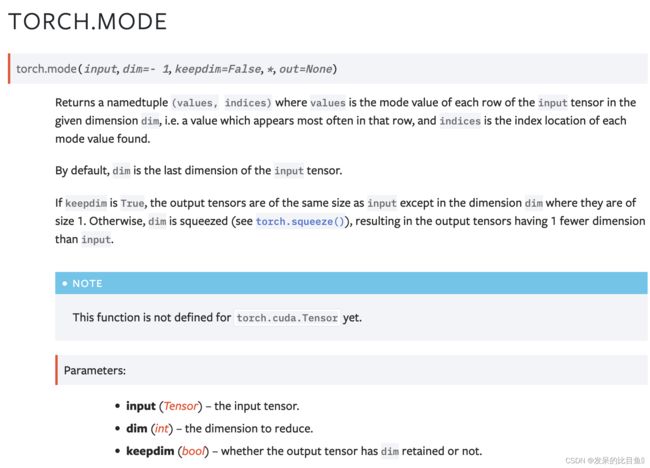
norm

返回给定张量的矩阵范数或向量范数。

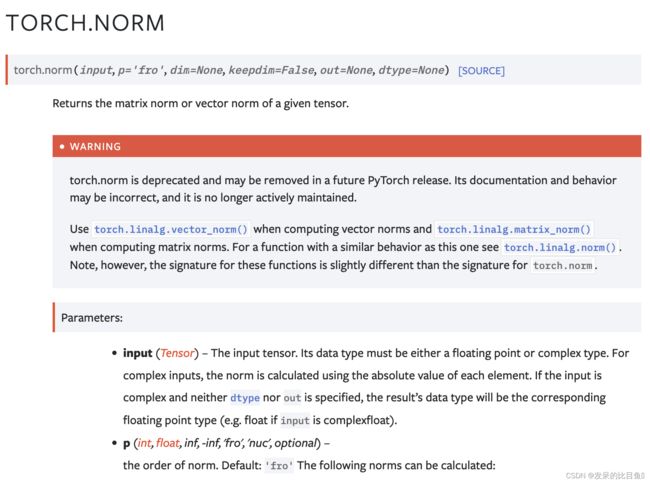
默认为p=‘fro’，计算矩阵的Frobenius norm (Frobenius 范数)，就是矩阵A各项元素的绝对值平方的总和，数学表达式为：$||A||=\sqrt{{\sum }_{i=1}^m{\sum }_{j=1}^n|a_{i,j}^2|}$
p='nuc’时，是求核范数，核范数是矩阵奇异值的和。（不常用）
常用的是第三种，p为int的形式,则是如下形式：

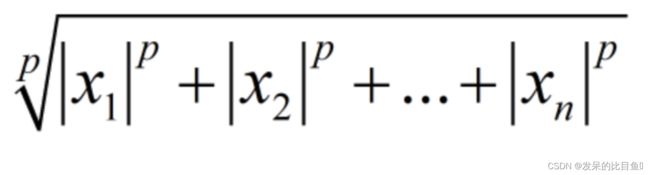
>>> import torch
>>> a = torch.arange(9, dtype= torch.float) - 4
>>> b = a.reshape((3, 3))
>>> torch.norm(a)
tensor(7.7460)
>>> torch.norm(b)
tensor(7.7460)
>>> torch.norm(a, float('inf'))
tensor(4.)
>>> torch.norm(b, float('inf'))
tensor(4.)
>>> c = torch.tensor([[ 1, 2, 3], [-1, 1, 4]] , dtype=torch.float)
>>> torch.norm(c, dim=0)
tensor([1.4142, 2.2361, 5.0000])
>>> torch.norm(c, dim=1)
tensor([3.7417, 4.2426])
>>> torch.norm(c, p=1, dim=1)
tensor([6., 6.])
>>> d = torch.arange(8, dtype=torch.float).reshape(2, 2, 2)
>>> torch.norm(d, dim=(1, 2))
tensor([ 3.7417, 11.2250])
>>> torch.norm(d[0, :, :]), torch.norm(d[1, :, :])
(tensor(3.7417), tensor(11.2250))

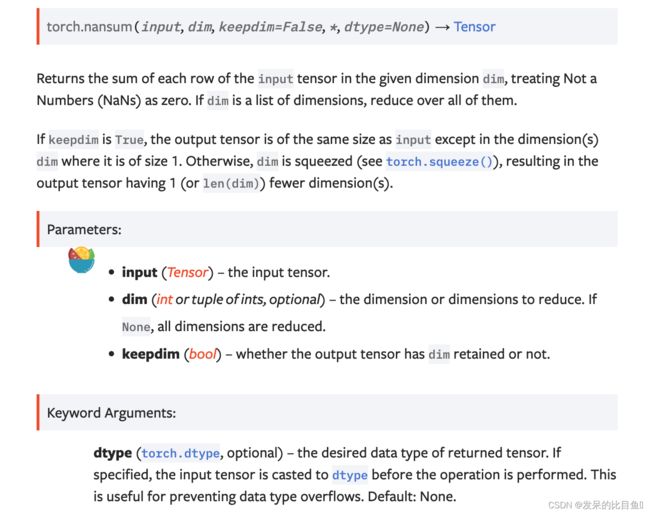
nansum

返回所有元素的总和，将非数字 (NaN) 视为零。

>>> a = torch.tensor([1., 2., float('nan'), 4.])
>>> torch.nansum(a)
tensor(7.)

>>> torch.nansum(torch.tensor([1., float("nan")]))
1.0
>>> a = torch.tensor([[1, 2], [3., float("nan")]])
>>> torch.nansum(a)
tensor(6.)
>>> torch.nansum(a, dim=0)
tensor([4., 2.])
>>> torch.nansum(a, dim=1)
tensor([3., 3.])

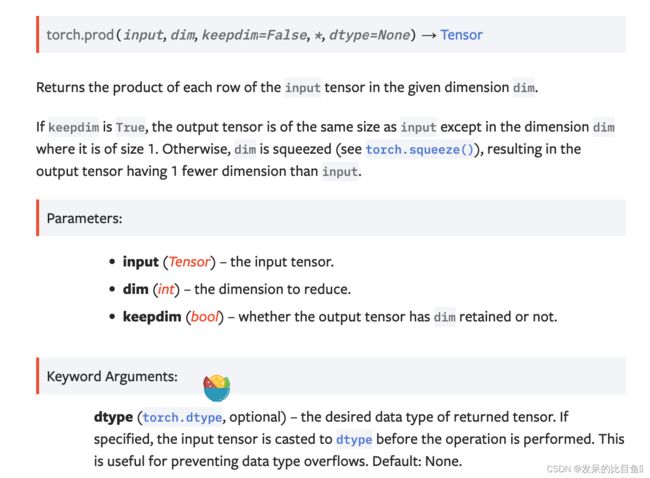
prod

返回输入张量中所有元素的乘积。

>>> a = torch.randn(1, 3)
>>> a
tensor([[-0.8020,  0.5428, -1.5854]])
>>> torch.prod(a)
tensor(0.6902)

>>> a = torch.randn(4, 2)
>>> a
tensor([[ 0.5261, -0.3837],
        [ 1.1857, -0.2498],
        [-1.1646,  0.0705],
        [ 1.1131, -1.0629]])
>>> torch.prod(a, 1)
tensor([-0.2018, -0.2962, -0.0821, -1.1831])

quantile

沿维度 dim 计算输入张量的每一行的第 q 个分位数。
为了计算分位数，我们将 [0, 1] 中的 q 映射到索引范围 [0, n] 以找到分位数在排序输入中的位置。如果分位数位于排序顺序为索引 i 和 j 的两个数据点 a < b 之间，则根据给定的插值方法计算结果，如下所示：
linear: a + (b - a) * fraction 其中fraction是计算分位数索引的小数部分。
lower: a.
higher: b.
nearest: a or b, 任何哪个索引都更接近计算的分位数索引（以0.5分数为单位）。
midpoint: (a + b) / 2.

>>> a = torch.randn(2, 3)
>>> a
tensor([[ 0.0795, -1.2117,  0.9765],
        [ 1.1707,  0.6706,  0.4884]])
>>> q = torch.tensor([0.25, 0.5, 0.75])
>>> torch.quantile(a, q, dim=1, keepdim=True)
tensor([[[-0.5661],
        [ 0.5795]],

        [[ 0.0795],
        [ 0.6706]],

        [[ 0.5280],
        [ 0.9206]]])
>>> torch.quantile(a, q, dim=1, keepdim=True).shape
torch.Size([3, 2, 1])
>>> a = torch.arange(4.)
>>> a
tensor([0., 1., 2., 3.])
>>> torch.quantile(a, 0.6, interpolation='linear')
tensor(1.8000)
>>> torch.quantile(a, 0.6, interpolation='lower')
tensor(1.)
>>> torch.quantile(a, 0.6, interpolation='higher')
tensor(2.)
>>> torch.quantile(a, 0.6, interpolation='midpoint')
tensor(1.5000)
>>> torch.quantile(a, 0.6, interpolation='nearest')
tensor(2.)
>>> torch.quantile(a, 0.4, interpolation='nearest')
tensor(1.)

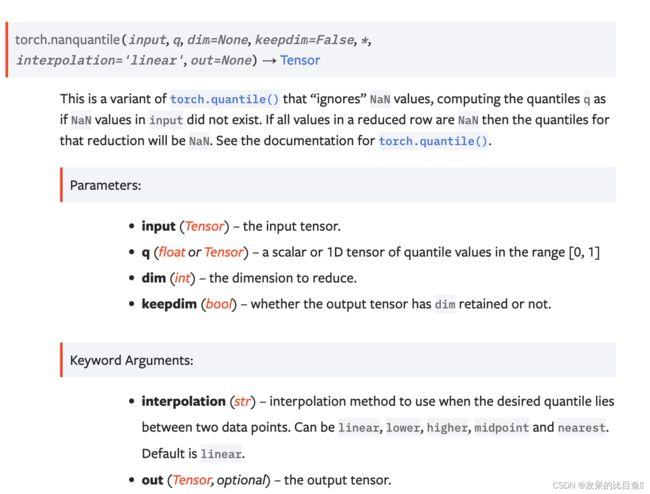
nanquantile

这是 torch.quantile() 的变体，它“忽略”NaN 值，计算分位数 q，就好像输入中的 NaN 值不存在一样。如果减少的行中的所有值都是 NaN，那么该减少的分位数将为 NaN。请参阅 torch.quantile() 的文档。

>>> t = torch.tensor([float('nan'), 1, 2])
>>> t.quantile(0.5)
tensor(nan)
>>> t.nanquantile(0.5)
tensor(1.5000)
>>> t = torch.tensor([[float('nan'), float('nan')], [1, 2]])
>>> t
tensor([[nan, nan],
        [1., 2.]])
>>> t.nanquantile(0.5, dim=0)
tensor([1., 2.])
>>> t.nanquantile(0.5, dim=1)
tensor([   nan, 1.5000])

std

计算 dim 指定的维度的标准偏差。 dim 可以是单个维度、维度列表或 None 以减少所有维度。

>>> a = torch.tensor(
...     [[ 0.2035,  1.2959,  1.8101, -0.4644],
...      [ 1.5027, -0.3270,  0.5905,  0.6538],
...      [-1.5745,  1.3330, -0.5596, -0.6548],
...      [ 0.1264, -0.5080,  1.6420,  0.1992]])
>>> torch.std(a, dim=1, keepdim=True)
tensor([[1.0311],
        [0.7477],
        [1.2204],
        [0.9087]])

std_mean

计算 dim 指定的维度的标准差和平均值。 dim 可以是单个维度、维度列表或 None 以减少所有维度。

>>> a = torch.tensor(
...     [[ 0.2035,  1.2959,  1.8101, -0.4644],
...      [ 1.5027, -0.3270,  0.5905,  0.6538],
...      [-1.5745,  1.3330, -0.5596, -0.6548],
...      [ 0.1264, -0.5080,  1.6420,  0.1992]])
>>> torch.std_mean(a, dim=0, keepdim=True)
(tensor([[1.2620, 1.0028, 1.0957, 0.6038]]),
 tensor([[ 0.0645,  0.4485,  0.8707, -0.0665]]))

sum

返回输入张量中所有元素的总和。

>>> a = torch.randn(1, 3)
>>> a
tensor([[ 0.1133, -0.9567,  0.2958]])
>>> torch.sum(a)
tensor(-0.5475)

unique

返回输入张量的唯一元素。

>>> output = torch.unique(torch.tensor([1, 3, 2, 3], dtype=torch.long))
>>> output
tensor([1, 2, 3])

>>> output, inverse_indices = torch.unique(
...     torch.tensor([1, 3, 2, 3], dtype=torch.long), sorted=True, return_inverse=True)
>>> output
tensor([1, 2, 3])
>>> inverse_indices
tensor([0, 2, 1, 2])

>>> output, inverse_indices = torch.unique(
...     torch.tensor([[1, 3], [2, 3]], dtype=torch.long), sorted=True, return_inverse=True)
>>> output
tensor([1, 2, 3])
>>> inverse_indices
tensor([[0, 2],
        [1, 2]])

unique_consecutive

从每组连续的等效元素中消除除第一个元素之外的所有元素。

input(Tensor): 输入张量。
return_inverse(bool): 是否也返回输入张量的元素在返回的output张量中的位置的索引。
return_counts(bool): 是否也返回每个值的出现次数。

>>> x = torch.tensor([1, 1, 2, 2, 3, 1, 1, 2])
>>> output = torch.unique_consecutive(x)
>>> output
tensor([1, 2, 3, 1, 2])

>>> output, inverse_indices = torch.unique_consecutive(x, return_inverse=True)
>>> output
tensor([1, 2, 3, 1, 2])
>>> inverse_indices
tensor([0, 0, 1, 1, 2, 3, 3, 4])

>>> output, counts = torch.unique_consecutive(x, return_counts=True)
>>> output
tensor([1, 2, 3, 1, 2])
>>> counts
tensor([2, 2, 1, 2, 1])

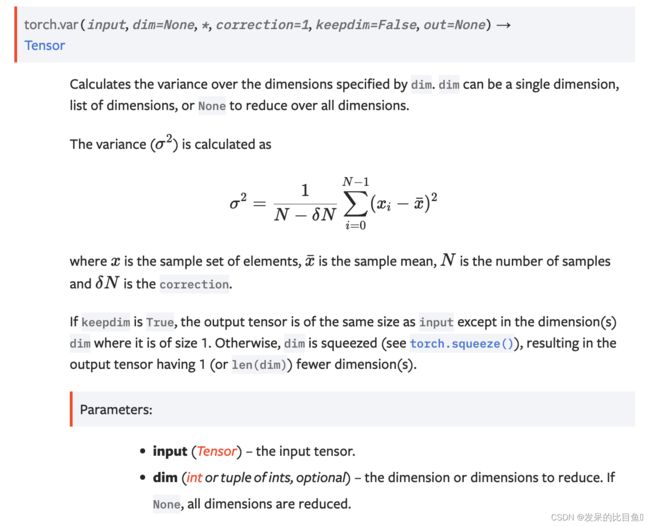
var

计算由 dim 指定的维度的方差。 dim 可以是单个维度、维度列表或 None 以减少所有维度。

>>> a = torch.tensor(
...     [[ 0.2035,  1.2959,  1.8101, -0.4644],
...      [ 1.5027, -0.3270,  0.5905,  0.6538],
...      [-1.5745,  1.3330, -0.5596, -0.6548],
...      [ 0.1264, -0.5080,  1.6420,  0.1992]])
>>> torch.var(a, dim=1, keepdim=True)
tensor([[1.0631],
        [0.5590],
        [1.4893],
        [0.8258]])

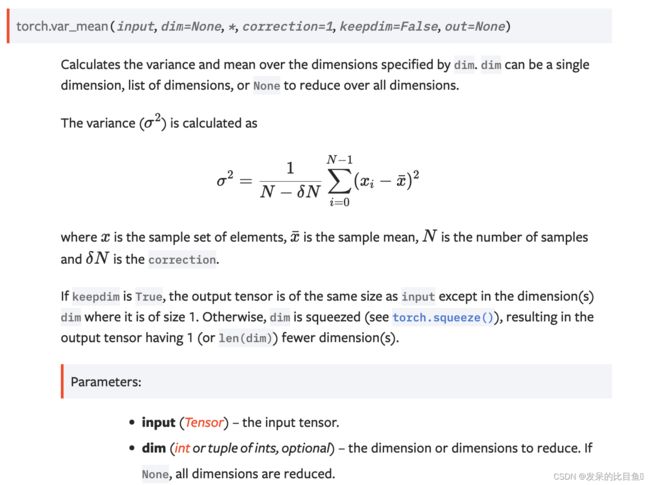
var_mean

计算 dim 指定的维度的方差和均值。 dim 可以是单个维度、维度列表或 None 以减少所有维度。

>>> a = torch.tensor(
...     [[ 0.2035,  1.2959,  1.8101, -0.4644],
...      [ 1.5027, -0.3270,  0.5905,  0.6538],
...      [-1.5745,  1.3330, -0.5596, -0.6548],
...      [ 0.1264, -0.5080,  1.6420,  0.1992]])
>>> torch.var_mean(a, dim=0, keepdim=True)
(tensor([[1.5926, 1.0056, 1.2005, 0.3646]]),
 tensor([[ 0.0645,  0.4485,  0.8707, -0.0665]]))

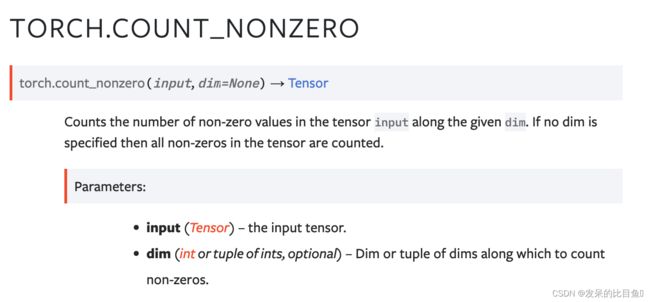
count_nonzero

沿给定的暗淡计算张量输入中非零值的数量。如果未指定暗淡，则计算张量中的所有非零值。

>>> x = torch.zeros(3,3)
>>> x[torch.randn(3,3) > 0.5] = 1
>>> x
tensor([[0., 1., 1.],
        [0., 0., 0.],
        [0., 0., 1.]])
>>> torch.count_nonzero(x)
tensor(3)
>>> torch.count_nonzero(x, dim=0)
tensor([0, 1, 2])