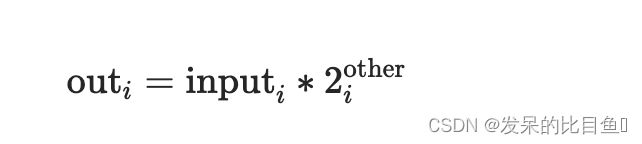发呆的比目鱼

小白学Pytorch系列-- Torch API (5)

Math operations

Pointwise Ops

TORCH.ABS

计算输入中每个元素的绝对值。

>>> torch.abs(torch.tensor([-1, -2, 3]))
tensor([ 1,  2,  3])

TORCH.ABSOLUTE

torch.abs() 的别名

TORCH.ACOS

计算输入中每个元素的逆余弦。

a = torch.randn(4)
a
torch.acos(a)

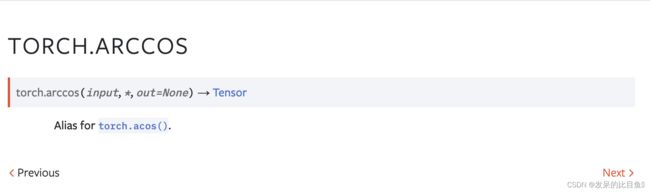
TORCH.ARCCOS

torch.acos()的别名。

TORCH.ACOSH

返回具有输入元素的反双曲余弦值的新张量。

TORCH.ARCCOSH

Torch.acosh() 的别名。

TORCH.ADD

将按 alpha 缩放的other添加到input。
![]](https://img-blog.csdnimg.cn/992cd8fd81ba4b209a07df9c0a3360a0.png)

>>> a = torch.randn(4)
>>> a
tensor([ 0.0202,  1.0985,  1.3506, -0.6056])
>>> torch.add(a, 20)
tensor([ 20.0202,  21.0985,  21.3506,  19.3944])

>>> b = torch.randn(4)
>>> b
tensor([-0.9732, -0.3497,  0.6245,  0.4022])
>>> c = torch.randn(4, 1)
>>> c
tensor([[ 0.3743],
        [-1.7724],
        [-0.5811],
        [-0.8017]])
>>> torch.add(b, c, alpha=10)
tensor([[  2.7695,   3.3930,   4.3672,   4.1450],
        [-18.6971, -18.0736, -17.0994, -17.3216],
        [ -6.7845,  -6.1610,  -5.1868,  -5.4090],
        [ -8.9902,  -8.3667,  -7.3925,  -7.6147]])

TORCH.ADDCDIV

执行 tensor1 除以 tensor2 的逐元素除法，将结果乘以标量值并将其添加到input。

t = torch.randn(1, 3)
t1 = torch.randn(3, 1)
t2 = torch.randn(1, 3)
torch.addcdiv(t, t1, t2, value=0.1)

TORCH.ADDCMUL

执行 tensor1 与 tensor2 的逐元素乘法，将结果乘以标量值并将其添加到input。

t = torch.randn(1, 3)
t1 = torch.randn(3, 1)
t2 = torch.randn(1, 3)
torch.addcmul(t, t1, t2, value=0.1)

TORCH.ANGLE

计算给定输入张量的元素角度（以弧度为单位）。

torch.angle(torch.tensor([-1 + 1j, -2 + 2j, 3 - 3j]))*180/3.14159

TORCH.ASIN

返回一个新的张量与输入元素的反正弦值。

a = torch.randn(4)
a
torch.asin(a)

TORCH.ARCSIN

torch.asin() 的别名。

TORCH.ASINH

返回具有输入元素的反双曲正弦值的新张量。

a = torch.randn(4)
a
torch.asinh(a)

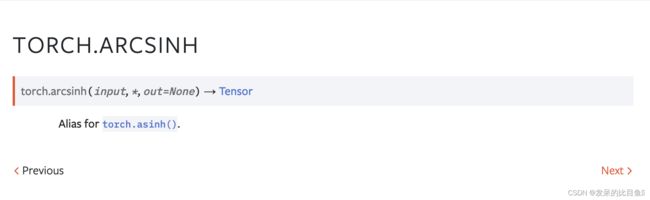
TORCH.ARCSINH

torch.asinh()的别名

TORCH.ATAN

返回一个新的张量与输入元素的反正切值。

a = torch.randn(4)
a
torch.atan(a)

TORCH.ARCTAN

torch.atan().别名

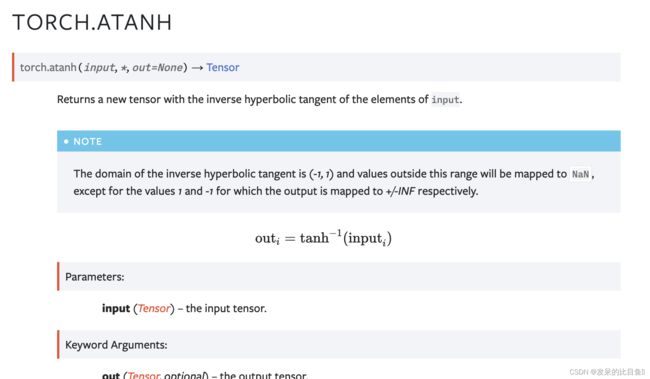
TORCH.ATANH

返回一个新的张量，该张量具有输入元素的反双曲正切。

>>> a = torch.randn(4).uniform_(-1, 1)
>>> a
tensor([ -0.9385, 0.2968, -0.8591, -0.1871 ])
>>> torch.atanh(a)
tensor([ -1.7253, 0.3060, -1.2899, -0.1893 ])

TORCH.ARCTANH

torch.atanh().别名

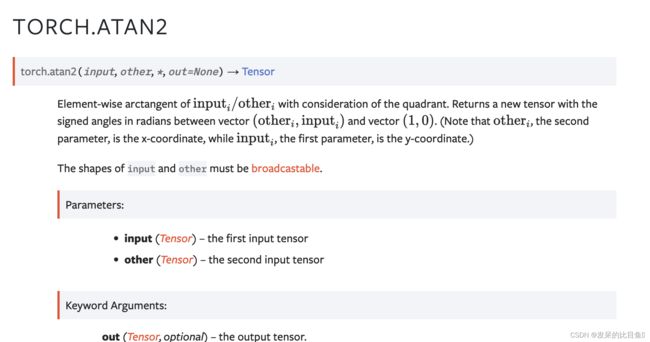
TORCH.ATAN2

考虑象限的input/other元素的反正切。返回一个新的张量，在向量（other，input）和向量（1,0）之间以弧度表示有符号的角度（注意第二个参数 other 是 x 坐标，而第一个参数 input 是 y-坐标。）

>>> a = torch.randn(4)
>>> a
tensor([ 0.9041,  0.0196, -0.3108, -2.4423])
>>> torch.atan2(a, torch.randn(4))
tensor([ 0.9833,  0.0811, -1.9743, -1.4151])

TORCH.ARCTAN2

torch.atan2() 别名。

TORCH.BITWISE_NOT

计算给定输入张量的按位非。输入张量必须是整数或布尔类型。对于 bool 张量，它计算逻辑 NOT。

>>> torch.bitwise_not(torch.tensor([-1, -2, 3], dtype=torch.int8))
tensor([ 0,  1, -4], dtype=torch.int8)

TORCH.BITWISE_AND

计算输入和其他的按位与。输入张量必须是整数或布尔类型。对于布尔张量，它计算逻辑与。

>>> torch.bitwise_and(torch.tensor([-1, -2, 3], dtype=torch.int8), torch.tensor([1, 0, 3], dtype=torch.int8))
tensor([1, 0,  3], dtype=torch.int8)
>>> torch.bitwise_and(torch.tensor([True, True, False]), torch.tensor([False, True, False]))
tensor([ False, True, False])

TORCH.BITWISE_OR

计算输入和其他的按位或。输入张量必须是整数或布尔类型。对于布尔张量，它计算逻辑或。

>>> torch.bitwise_or(torch.tensor([-1, -2, 3], dtype=torch.int8), torch.tensor([1, 0, 3], dtype=torch.int8))
tensor([-1, -2,  3], dtype=torch.int8)
>>> torch.bitwise_or(torch.tensor([True, True, False]), torch.tensor([False, True, False]))
tensor([ True, True, False])

TORCH.BITWISE_XOR

计算输入和其他的按位异或。输入张量必须是整数或布尔类型。对于 bool 张量，它计算逻辑 XOR。

>>> torch.bitwise_xor(torch.tensor([-1, -2, 3], dtype=torch.int8), torch.tensor([1, 0, 3], dtype=torch.int8))
tensor([-2, -2,  0], dtype=torch.int8)
>>> torch.bitwise_xor(torch.tensor([True, True, False]), torch.tensor([False, True, False]))
tensor([ True, False, False])

TORCH.BITWISE_LEFT_SHIFT

计算输入的其他位的左算术移位。输入张量必须是整数类型。此运营商支持广播到一个共同的形状和类型推广。

>>> torch.bitwise_left_shift(torch.tensor([-1, -2, 3], dtype=torch.int8), torch.tensor([1, 0, 3], dtype=torch.int8))
tensor([-2, -2, 24], dtype=torch.int8)

TORCH.BITWISE_RIGHT_SHIFT

计算其他位输入的算术右移。输入张量必须是积分类型。该运营商支持以普通形状和类型进行广播推广。

>>> torch.bitwise_right_shift(torch.tensor([-2, -7, 31], dtype=torch.int8), torch.tensor([1, 0, 3], dtype=torch.int8))
tensor([-1, -7,  3], dtype=torch.int8)

TORCH.CEIL

返回一个新的张量，其中包含输入元素的 ceil，即大于或等于每个元素的最小整数。

对于整数输入，遵循返回输入张量副本的 array-api 约定。

>>> a = torch.randn(4)
>>> a
tensor([-0.6341, -1.4208, -1.0900,  0.5826])
>>> torch.ceil(a)
tensor([-0., -1., -1.,  1.])

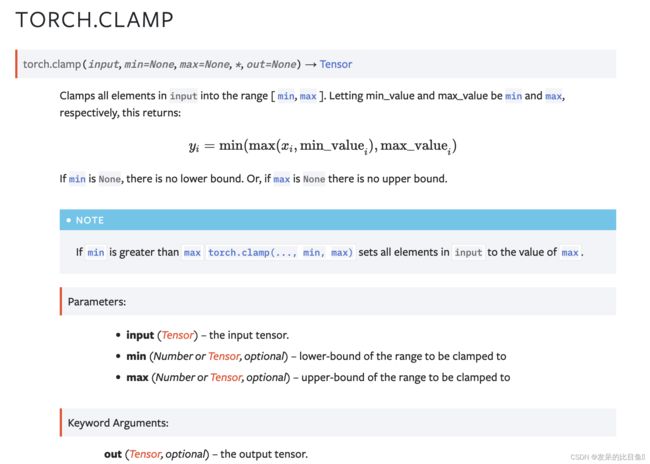
TORCH.CLAMP

将 input 中的所有元素限制在 [ min, max ] 范围内。令 min_value 和 max_value 分别为最小值和最大值，返回：

>>> a = torch.randn(4)
>>> a
tensor([-1.7120,  0.1734, -0.0478, -0.0922])
>>> torch.clamp(a, min=-0.5, max=0.5)
tensor([-0.5000,  0.1734, -0.0478, -0.0922])

>>> min = torch.linspace(-1, 1, steps=4)
>>> torch.clamp(a, min=min)
tensor([-1.0000,  0.1734,  0.3333,  1.0000])

TORCH.CLIP

torch.clamp() 的别名。

TORCH.CONJ_PHYSICAL

计算给定输入张量的逐元素共轭。如果输入有一个非复杂数据类型，这个函数只返回输入。

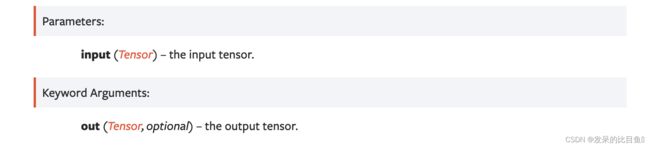
>>> torch.conj_physical(torch.tensor([-1 + 1j, -2 + 2j, 3 - 3j]))
tensor([-1 - 1j, -2 - 2j, 3 + 3j])

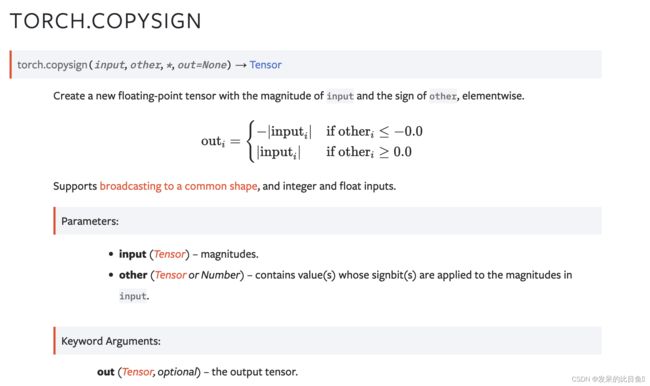
TORCH.COPYSIGN

创建一个新的浮点张量，具有输入的大小和其他元素的符号。

>>> a = torch.randn(5)
>>> a
tensor([-1.2557, -0.0026, -0.5387,  0.4740, -0.9244])
>>> torch.copysign(a, 1)
tensor([1.2557, 0.0026, 0.5387, 0.4740, 0.9244])
>>> a = torch.randn(4, 4)
>>> a
tensor([[ 0.7079,  0.2778, -1.0249,  0.5719],
        [-0.0059, -0.2600, -0.4475, -1.3948],
        [ 0.3667, -0.9567, -2.5757, -0.1751],
        [ 0.2046, -0.0742,  0.2998, -0.1054]])
>>> b = torch.randn(4)
tensor([ 0.2373,  0.3120,  0.3190, -1.1128])
>>> torch.copysign(a, b)
tensor([[ 0.7079,  0.2778,  1.0249, -0.5719],
        [ 0.0059,  0.2600,  0.4475, -1.3948],
        [ 0.3667,  0.9567,  2.5757, -0.1751],
        [ 0.2046,  0.0742,  0.2998, -0.1054]])
>>> a = torch.tensor([1.])
>>> b = torch.tensor([-0.])
>>> torch.copysign(a, b)
tensor([-1.])

TORCH.COS

返回一个新的张量与输入元素的余弦值。

>>> a = torch.randn(4)
>>> a
tensor([ 1.4309,  1.2706, -0.8562,  0.9796])
>>> torch.cos(a)
tensor([ 0.1395,  0.2957,  0.6553,  0.5574])

TORCH.COSH

返回具有输入元素的双曲余弦值的新张量。

>>> a = torch.randn(4)
>>> a
tensor([ 0.1632,  1.1835, -0.6979, -0.7325])
>>> torch.cosh(a)
tensor([ 1.0133,  1.7860,  1.2536,  1.2805])

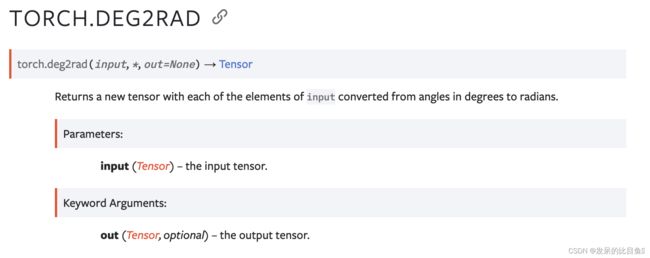
TORCH.DEG2RAD

返回一个新的张量，其中输入的每个元素都从以度为单位的角度转换为弧度。

>>> a = torch.tensor([[180.0, -180.0], [360.0, -360.0], [90.0, -90.0]])
>>> torch.deg2rad(a)
tensor([[ 3.1416, -3.1416],
        [ 6.2832, -6.2832],
        [ 1.5708, -1.5708]])

TORCH.DIV

将输入 input 的每个元素除以 other 的对应元素。

>>> x = torch.tensor([ 0.3810,  1.2774, -0.2972, -0.3719,  0.4637])
>>> torch.div(x, 0.5)
tensor([ 0.7620,  2.5548, -0.5944, -0.7438,  0.9274])

>>> a = torch.tensor([[-0.3711, -1.9353, -0.4605, -0.2917],
...                   [ 0.1815, -1.0111,  0.9805, -1.5923],
...                   [ 0.1062,  1.4581,  0.7759, -1.2344],
...                   [-0.1830, -0.0313,  1.1908, -1.4757]])
>>> b = torch.tensor([ 0.8032,  0.2930, -0.8113, -0.2308])
>>> torch.div(a, b)
tensor([[-0.4620, -6.6051,  0.5676,  1.2639],
        [ 0.2260, -3.4509, -1.2086,  6.8990],
        [ 0.1322,  4.9764, -0.9564,  5.3484],
        [-0.2278, -0.1068, -1.4678,  6.3938]])

>>> torch.div(a, b, rounding_mode='trunc')
tensor([[-0., -6.,  0.,  1.],
        [ 0., -3., -1.,  6.],
        [ 0.,  4., -0.,  5.],
        [-0., -0., -1.,  6.]])

>>> torch.div(a, b, rounding_mode='floor')
tensor([[-1., -7.,  0.,  1.],
        [ 0., -4., -2.,  6.],
        [ 0.,  4., -1.,  5.],
        [-1., -1., -2.,  6.]])

TORCH.DIVIDE

torch.div() 的别名

TORCH.DIGAMMA

Torch.special.digamma()的别名。

TORCH.ERF

torch.special.erf()的别名。

TORCH.ERFC

Torch.special.erfc() 的别名。

TORCH.ERFINV

torch.special.erfinv()的别名。

TORCH.EXP

返回一个新的张量，其中包含输入张量 input 的元素的指数。

>>> torch.exp(torch.tensor([0, math.log(2.)]))
tensor([ 1.,  2.])

TORCH.EXP2

torch.special.exp2().别名

TORCH.EXPM1

torch.special.expm1().别名

>>> torch.special.expm1(torch.tensor([0, math.log(2.)]))
tensor([ 0.,  1.])

TORCH.FAKE_QUANTIZE_PER_CHANNEL_AFFINE

返回一个新的张量，其中输入伪造中的数据在 axis 指定的通道中使用 scale、zero_point、quant_min 和 quant_max 按通道量化。

>>> x = torch.randn(2, 2, 2)
>>> x
tensor([[[-0.2525, -0.0466],
         [ 0.3491, -0.2168]],

        [[-0.5906,  1.6258],
         [ 0.6444, -0.0542]]])
>>> scales = (torch.randn(2) + 1) * 0.05
>>> scales
tensor([0.0475, 0.0486])
>>> zero_points = torch.zeros(2).to(torch.int32)
>>> zero_points
tensor([0, 0])
>>> torch.fake_quantize_per_channel_affine(x, scales, zero_points, 1, 0, 255)
tensor([[[0.0000, 0.0000],
         [0.3405, 0.0000]],

        [[0.0000, 1.6134],
        [0.6323, 0.0000]]])

TORCH.FAKE_QUANTIZE_PER_TENSOR_AFFINE

返回一个新的张量，其中使用 scale、zero_point、quant_min 和 quant_max 量化了输入伪造中的数据。

>>> x = torch.randn(4)
>>> x
tensor([ 0.0552,  0.9730,  0.3973, -1.0780])
>>> torch.fake_quantize_per_tensor_affine(x, 0.1, 0, 0, 255)
tensor([0.1000, 1.0000, 0.4000, 0.0000])
>>> torch.fake_quantize_per_tensor_affine(x, torch.tensor(0.1), torch.tensor(0), 0, 255)
tensor([0.6000, 0.4000, 0.0000, 0.0000])

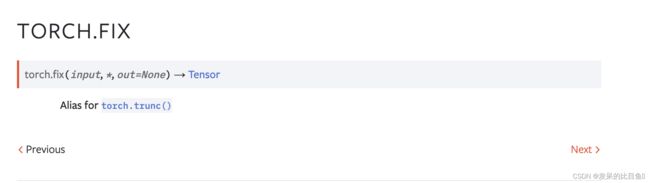
TORCH.FIX

返回一个新的张量，其中包含输入元素的截断整数值。
对于整数输入，遵循返回输入张量副本的 array-api 约定。

>>> a = torch.randn(4)
>>> a
tensor([ 3.4742,  0.5466, -0.8008, -0.9079])
>>> torch.trunc(a)
tensor([ 3.,  0., -0., -0.])

TORCH.FLOAT_POWER

以双精度按元素将输入提高到指数的幂。如果两个输入都不是复数，则返回 torch.float64 张量，如果一个或多个输入是复数，则返回 torch.complex128 张量。

>>> a = torch.randint(10, (4,))
>>> a
tensor([6, 4, 7, 1])
>>> torch.float_power(a, 2)
tensor([36., 16., 49.,  1.], dtype=torch.float64)

>>> a = torch.arange(1, 5)
>>> a
tensor([ 1,  2,  3,  4])
>>> exp = torch.tensor([2, -3, 4, -5])
>>> exp
tensor([ 2, -3,  4, -5])
>>> torch.float_power(a, exp)
tensor([1.0000e+00, 1.2500e-01, 8.1000e+01, 9.7656e-04], dtype=torch.float64)

TORCH.FLOOR

返回一个新的张量，其中包含输入元素的底数，小于或等于每个元素的最大整数。

对于整数输入，遵循返回输入张量副本的 array-api 约定。

>>> a = torch.randn(4)
>>> a
tensor([-0.8166,  1.5308, -0.2530, -0.2091])
>>> torch.floor(a)
tensor([-1.,  1., -1., -1.])

TORCH.FLOOR_DIVIDE

计算输入除以其他元素，然后计算结果。

>>> a = torch.tensor([4.0, 3.0])
>>> b = torch.tensor([2.0, 2.0])
>>> torch.floor_divide(a, b)
tensor([2.0, 1.0])
>>> torch.floor_divide(a, 1.4)
tensor([2.0, 2.0])

TORCH.FMOD

在入口处应用 C++ 的 std::fmod。结果与被除数输入同号且绝对值小于other。

>>> torch.fmod(torch.tensor([-3., -2, -1, 1, 2, 3]), 2)
tensor([-1., -0., -1.,  1.,  0.,  1.])
>>> torch.fmod(torch.tensor([1, 2, 3, 4, 5]), -1.5)
tensor([1.0000, 0.5000, 0.0000, 1.0000, 0.5000])

TORCH.FRAC

计算输入中每个元素的小数部分。

>>> torch.frac(torch.tensor([1, 2.5, -3.2]))
tensor([ 0.0000,  0.5000, -0.2000])

TORCH.FREXP

将输入分解为尾数和指数张量，使得 $输入=尾数×2^{指数}$

>>> x = torch.arange(9.)
>>> mantissa, exponent = torch.frexp(x)
>>> mantissa
tensor([0.0000, 0.5000, 0.5000, 0.7500, 0.5000, 0.6250, 0.7500, 0.8750, 0.5000])
>>> exponent
tensor([0, 1, 2, 2, 3, 3, 3, 3, 4], dtype=torch.int32)
>>> torch.ldexp(mantissa, exponent)
tensor([0., 1., 2., 3., 4., 5., 6., 7., 8.])

TORCH.GRADIENT

>>> # Estimates the gradient of f(x)=x^2 at points [-2, -1, 2, 4]
>>> coordinates = (torch.tensor([-2., -1., 1., 4.]),)
>>> values = torch.tensor([4., 1., 1., 16.], )
>>> torch.gradient(values, spacing = coordinates)
(tensor([-3., -2., 2., 5.]),)

>>> # Estimates the gradient of the R^2 -> R function whose samples are
>>> # described by the tensor t. Implicit coordinates are [0, 1] for the outermost
>>> # dimension and [0, 1, 2, 3] for the innermost dimension, and function estimates
>>> # partial derivative for both dimensions.
>>> t = torch.tensor([[1, 2, 4, 8], [10, 20, 40, 80]])
>>> torch.gradient(t)
(tensor([[ 9., 18., 36., 72.],
         [ 9., 18., 36., 72.]]),
 tensor([[ 1.0000, 1.5000, 3.0000, 4.0000],
         [10.0000, 15.0000, 30.0000, 40.0000]]))

>>> # A scalar value for spacing modifies the relationship between tensor indices
>>> # and input coordinates by multiplying the indices to find the
>>> # coordinates. For example, below the indices of the innermost
>>> # 0, 1, 2, 3 translate to coordinates of [0, 2, 4, 6], and the indices of
>>> # the outermost dimension 0, 1 translate to coordinates of [0, 2].
>>> torch.gradient(t, spacing = 2.0) # dim = None (implicitly [0, 1])
(tensor([[ 4.5000, 9.0000, 18.0000, 36.0000],
          [ 4.5000, 9.0000, 18.0000, 36.0000]]),
 tensor([[ 0.5000, 0.7500, 1.5000, 2.0000],
          [ 5.0000, 7.5000, 15.0000, 20.0000]]))
>>> # doubling the spacing between samples halves the estimated partial gradients.

>>>
>>> # Estimates only the partial derivative for dimension 1
>>> torch.gradient(t, dim = 1) # spacing = None (implicitly 1.)
(tensor([[ 1.0000, 1.5000, 3.0000, 4.0000],
         [10.0000, 15.0000, 30.0000, 40.0000]]),)

>>> # When spacing is a list of scalars, the relationship between the tensor
>>> # indices and input coordinates changes based on dimension.
>>> # For example, below, the indices of the innermost dimension 0, 1, 2, 3 translate
>>> # to coordinates of [0, 3, 6, 9], and the indices of the outermost dimension
>>> # 0, 1 translate to coordinates of [0, 2].
>>> torch.gradient(t, spacing = [3., 2.])
(tensor([[ 4.5000, 9.0000, 18.0000, 36.0000],
         [ 4.5000, 9.0000, 18.0000, 36.0000]]),
 tensor([[ 0.3333, 0.5000, 1.0000, 1.3333],
         [ 3.3333, 5.0000, 10.0000, 13.3333]]))

>>> # The following example is a replication of the previous one with explicit
>>> # coordinates.
>>> coords = (torch.tensor([0, 2]), torch.tensor([0, 3, 6, 9]))
>>> torch.gradient(t, spacing = coords)
(tensor([[ 4.5000, 9.0000, 18.0000, 36.0000],
         [ 4.5000, 9.0000, 18.0000, 36.0000]]),
 tensor([[ 0.3333, 0.5000, 1.0000, 1.3333],
         [ 3.3333, 5.0000, 10.0000, 13.3333]]))

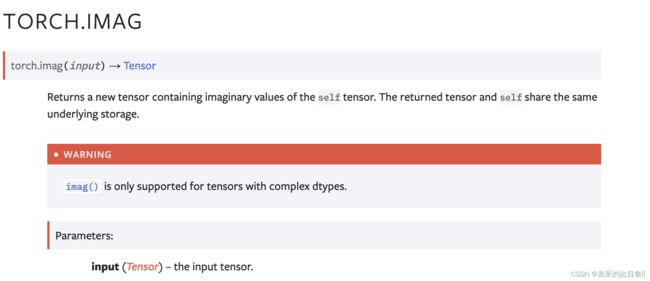
TORCH.IMAG

返回一个包含自张量的虚数值的新张量。返回的张量和 self 共享相同的底层存储。

>>> x=torch.randn(4, dtype=torch.cfloat)
>>> x
tensor([(0.3100+0.3553j), (-0.5445-0.7896j), (-1.6492-0.0633j), (-0.0638-0.8119j)])
>>> x.imag
tensor([ 0.3553, -0.7896, -0.0633, -0.8119])

TORCH.LDEXP

将输入乘以 2 ** other。

通常，此函数用于通过将输入中的尾数与从其他中的指数创建的两个整数幂相乘来构造浮点数。

>>> torch.ldexp(torch.tensor([1.]), torch.tensor([1]))
tensor([2.])
>>> torch.ldexp(torch.tensor([1.0]), torch.tensor([1, 2, 3, 4]))
tensor([ 2.,  4.,  8., 16.])

TORCH.LERP

两个张量的线性插值是否开始（由输入给出）并基于标量或张量权重结束并返回结果张量。

>>> start = torch.arange(1., 5.)
>>> end = torch.empty(4).fill_(10)
>>> start
tensor([ 1.,  2.,  3.,  4.])
>>> end
tensor([ 10.,  10.,  10.,  10.])
>>> torch.lerp(start, end, 0.5)
tensor([ 5.5000,  6.0000,  6.5000,  7.0000])
>>> torch.lerp(start, end, torch.full_like(start, 0.5))
tensor([ 5.5000,  6.0000,  6.5000,  7.0000])

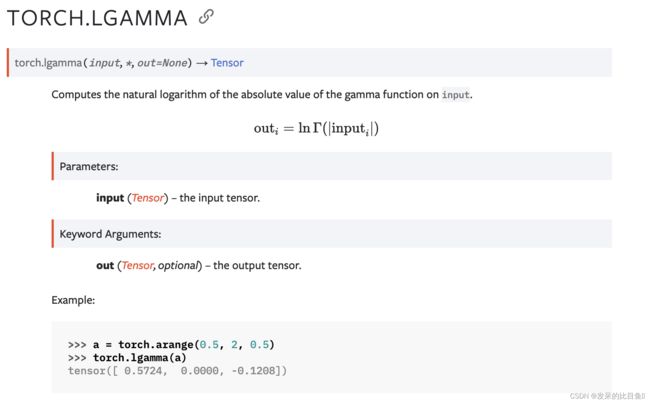
TORCH.LGAMMA

计算输入的 gamma 函数的绝对值的自然对数。

>>> a = torch.arange(0.5, 2, 0.5)
>>> torch.lgamma(a)
tensor([ 0.5724,  0.0000, -0.1208])

TORCH.LOG

返回具有输入元素自然对数的新张量。

>>> a = torch.rand(5) * 5
>>> a
tensor([4.7767, 4.3234, 1.2156, 0.2411, 4.5739])
>>> torch.log(a)
tensor([ 1.5637,  1.4640,  0.1952, -1.4226,  1.5204])

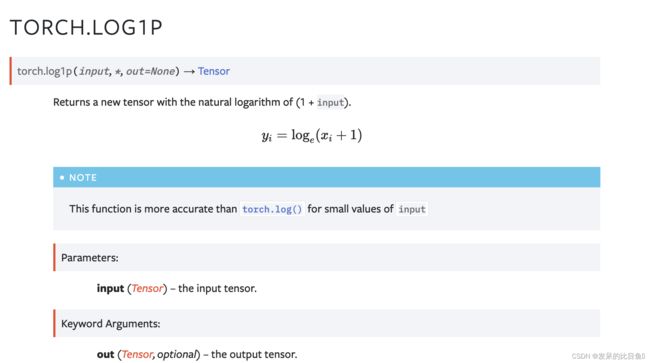
TORCH.LOG1P

返回具有 (1 + input) 自然对数的新张量。

>>> a = torch.randn(5)
>>> a
tensor([-1.0090, -0.9923,  1.0249, -0.5372,  0.2492])
>>> torch.log1p(a)
tensor([    nan, -4.8653,  0.7055, -0.7705,  0.2225])

TORCH.LOG2

返回一个新的张量，其对数为输入元素的底 2。

>>> a = torch.rand(5)
>>> a
tensor([ 0.8419,  0.8003,  0.9971,  0.5287,  0.0490])


>>> torch.log2(a)
tensor([-0.2483, -0.3213, -0.0042, -0.9196, -4.3504])

TORCH.LOGADDEXP

输入的指数总和的对数。
计算逐点对数 $e^x +e^y)$ 。此函数在统计中很有用，其中计算的事件概率可能小到超出正常浮点数的范围。在这种情况下，存储计算概率的对数。此函数允许添加以这种方式存储的概率。

此操作应与 torch.logsumexp() 消除歧义，后者对单个张量执行缩减。

>>> torch.logaddexp(torch.tensor([-1.0]), torch.tensor([-1.0, -2, -3]))
tensor([-0.3069, -0.6867, -0.8731])
>>> torch.logaddexp(torch.tensor([-100.0, -200, -300]), torch.tensor([-1.0, -2, -3]))
tensor([-1., -2., -3.])
>>> torch.logaddexp(torch.tensor([1.0, 2000, 30000]), torch.tensor([-1.0, -2, -3]))
tensor([1.1269e+00, 2.0000e+03, 3.0000e+04])

TORCH.LOGADDEXP2

以 2 为基数的输入的指数总和的对数。
计算逐点 $log2 (2^x+2^y)$ 。有关详细信息，请参阅 torch.logaddexp()。

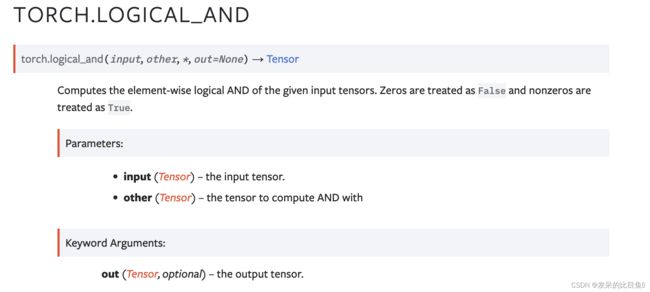
TORCH.LOGICAL_AND

计算给定输入张量的逐元素逻辑与。零被视为假，非零被视为真。

>>> torch.logical_and(torch.tensor([True, False, True]), torch.tensor([True, False, False]))
tensor([ True, False, False])
>>> a = torch.tensor([0, 1, 10, 0], dtype=torch.int8)
>>> b = torch.tensor([4, 0, 1, 0], dtype=torch.int8)
>>> torch.logical_and(a, b)
tensor([False, False,  True, False])
>>> torch.logical_and(a.double(), b.double())
tensor([False, False,  True, False])
>>> torch.logical_and(a.double(), b)
tensor([False, False,  True, False])
>>> torch.logical_and(a, b, out=torch.empty(4, dtype=torch.bool))
tensor([False, False,  True, False])

TORCH.LOGICAL_NOT

计算给定输入张量的逐元素逻辑非。如果未指定，输出张量将具有 bool dtype。如果输入张量不是 bool 张量，则将零视为 False，将非零视为 True。

>>> torch.logical_not(torch.tensor([True, False]))
tensor([False,  True])
>>> torch.logical_not(torch.tensor([0, 1, -10], dtype=torch.int8))
tensor([ True, False, False])
>>> torch.logical_not(torch.tensor([0., 1.5, -10.], dtype=torch.double))
tensor([ True, False, False])
>>> torch.logical_not(torch.tensor([0., 1., -10.], dtype=torch.double), out=torch.empty(3, dtype=torch.int16))
tensor([1, 0, 0], dtype=torch.int16)

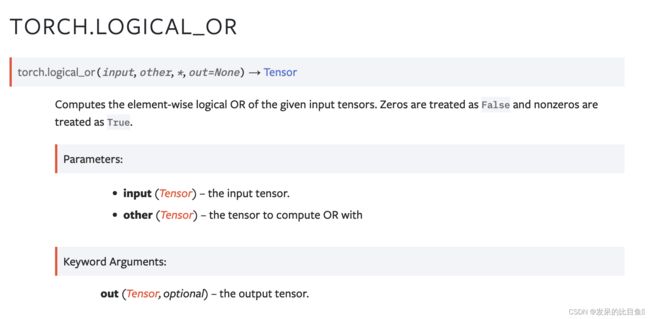
TORCH.LOGICAL_OR

计算给定输入张量的逐元素逻辑或。零被视为假，非零被视为真。

>>> torch.logical_or(torch.tensor([True, False, True]), torch.tensor([True, False, False]))
tensor([ True, False,  True])
>>> a = torch.tensor([0, 1, 10, 0], dtype=torch.int8)
>>> b = torch.tensor([4, 0, 1, 0], dtype=torch.int8)
>>> torch.logical_or(a, b)
tensor([ True,  True,  True, False])
>>> torch.logical_or(a.double(), b.double())
tensor([ True,  True,  True, False])
>>> torch.logical_or(a.double(), b)
tensor([ True,  True,  True, False])
>>> torch.logical_or(a, b, out=torch.empty(4, dtype=torch.bool))
tensor([ True,  True,  True, False])

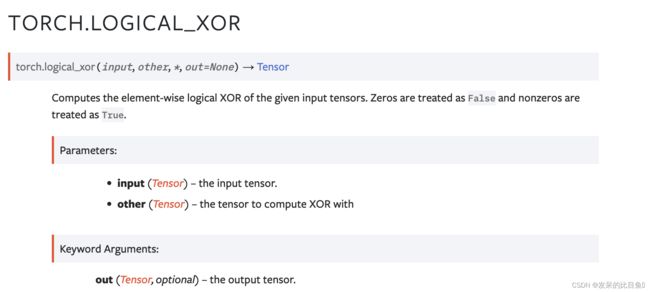
TORCH.LOGICAL_XOR

计算给定输入张量的逐元素逻辑异或。零被视为假，非零被视为真。

>>> torch.logical_xor(torch.tensor([True, False, True]), torch.tensor([True, False, False]))
tensor([False, False,  True])
>>> a = torch.tensor([0, 1, 10, 0], dtype=torch.int8)
>>> b = torch.tensor([4, 0, 1, 0], dtype=torch.int8)
>>> torch.logical_xor(a, b)
tensor([ True,  True, False, False])
>>> torch.logical_xor(a.double(), b.double())
tensor([ True,  True, False, False])
>>> torch.logical_xor(a.double(), b)
tensor([ True,  True, False, False])
>>> torch.logical_xor(a, b, out=torch.empty(4, dtype=torch.bool))
tensor([ True,  True, False, False])

TORCH.LOGIT

>>> a = torch.rand(5)
>>> a
tensor([0.2796, 0.9331, 0.6486, 0.1523, 0.6516])
>>> torch.special.logit(a, eps=1e-6)
tensor([-0.9466,  2.6352,  0.6131, -1.7169,  0.6261])

TORCH.HYPOT

给定一个直角三角形的边，返回它的斜边。

>>> a = torch.hypot(torch.tensor([4.0]), torch.tensor([3.0, 4.0, 5.0]))
tensor([5.0000, 5.6569, 6.4031])

TORCH.I0

torch.special.i0().别名

>>> torch.i0(torch.arange(5, dtype=torch.float32))
tensor([ 1.0000,  1.2661,  2.2796,  4.8808, 11.3019])

TORCH.IGAMMA

torch.special.gammainc().别名

>>> a1 = torch.tensor([4.0])
>>> a2 = torch.tensor([3.0, 4.0, 5.0])
>>> a = torch.special.gammaincc(a1, a2)
tensor([0.3528, 0.5665, 0.7350])
tensor([0.3528, 0.5665, 0.7350])
>>> b = torch.special.gammainc(a1, a2) + torch.special.gammaincc(a1, a2)
tensor([1., 1., 1.])

TORCH.IGAMMAC

torch.special.gammaincc().别名

>>> a1 = torch.tensor([4.0])
>>> a2 = torch.tensor([3.0, 4.0, 5.0])
>>> a = torch.special.gammaincc(a1, a2)
tensor([0.6472, 0.4335, 0.2650])
>>> b = torch.special.gammainc(a1, a2) + torch.special.gammaincc(a1, a2)
tensor([1., 1., 1.])

TORCH.MUL

>>> a = torch.randn(3)
>>> a
tensor([ 0.2015, -0.4255,  2.6087])
>>> torch.mul(a, 100)
tensor([  20.1494,  -42.5491,  260.8663])

>>> b = torch.randn(4, 1)
>>> b
tensor([[ 1.1207],
        [-0.3137],
        [ 0.0700],
        [ 0.8378]])
>>> c = torch.randn(1, 4)
>>> c
tensor([[ 0.5146,  0.1216, -0.5244,  2.2382]])
>>> torch.mul(b, c)
tensor([[ 0.5767,  0.1363, -0.5877,  2.5083],
        [-0.1614, -0.0382,  0.1645, -0.7021],
        [ 0.0360,  0.0085, -0.0367,  0.1567],
        [ 0.4312,  0.1019, -0.4394,  1.8753]])

TORCH.MULTIPLY

torch.mul().别名

TORCH.MVLGAMMA

torch.special.multigammaln()别名

TORCH.NAN_TO_NUM

分别用 nan、posinf 和 neginf 指定的值替换输入中的 NaN、正无穷大和负无穷大值。默认情况下，NaN 替换为零，正无穷大替换为输入数据类型可表示的最大有限值，负无穷大替换为输入数据类型可表示的最小有限值。

>>> x = torch.tensor([float('nan'), float('inf'), -float('inf'), 3.14])
>>> torch.nan_to_num(x)
tensor([ 0.0000e+00,  3.4028e+38, -3.4028e+38,  3.1400e+00])
>>> torch.nan_to_num(x, nan=2.0)
tensor([ 2.0000e+00,  3.4028e+38, -3.4028e+38,  3.1400e+00])
>>> torch.nan_to_num(x, nan=2.0, posinf=1.0)
tensor([ 2.0000e+00,  1.0000e+00, -3.4028e+38,  3.1400e+00])

TORCH.NEG

返回具有输入元素负值的新张量。

>>> a = torch.randn(5)
>>> a
tensor([ 0.0090, -0.2262, -0.0682, -0.2866,  0.3940])
>>> torch.neg(a)
tensor([-0.0090,  0.2262,  0.0682,  0.2866, -0.3940])

TORCH.NEGATIVE

torch.neg()别名

TORCH.NEXTAFTER

在向其他元素输入后返回下一个浮点值。

input 和 other 的形状必须是可广播的。

>>> eps = torch.finfo(torch.float32).eps
>>> torch.nextafter(torch.tensor([1.0, 2.0]), torch.tensor([2.0, 1.0])) == torch.tensor([eps + 1, 2 - eps])
tensor([True, True])

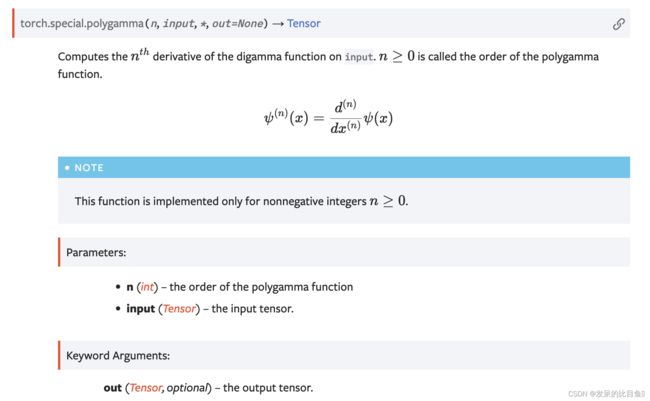
TORCH.POLYGAMMA

计算输入的 digamma 函数的 th 导数。n≥0称为多伽马函数的阶数。

>>> a = torch.tensor([1, 0.5])
>>> torch.special.polygamma(1, a)
tensor([1.64493, 4.9348])
>>> torch.special.polygamma(2, a)
tensor([ -2.4041, -16.8288])
>>> torch.special.polygamma(3, a)
tensor([ 6.4939, 97.4091])
>>> torch.special.polygamma(4, a)
tensor([ -24.8863, -771.4742])

TORCH.POSITIVE

返回输入。如果输入是 bool 张量，则抛出运行时错误。

>>> t = torch.randn(5)
>>> t
tensor([ 0.0090, -0.2262, -0.0682, -0.2866,  0.3940])
>>> torch.positive(t)
tensor([ 0.0090, -0.2262, -0.0682, -0.2866,  0.3940])

TORCH.POW

取输入中每个元素的幂和指数，并返回张量和结果。

指数可以是单个浮点数或具有与输入相同数量的元素的张量。

>>> a = torch.randn(4)
>>> a
tensor([ 0.4331,  1.2475,  0.6834, -0.2791])
>>> torch.pow(a, 2)
tensor([ 0.1875,  1.5561,  0.4670,  0.0779])
>>> exp = torch.arange(1., 5.)

>>> a = torch.arange(1., 5.)
>>> a
tensor([ 1.,  2.,  3.,  4.])
>>> exp
tensor([ 1.,  2.,  3.,  4.])
>>> torch.pow(a, exp)
tensor([   1.,    4.,   27.,  256.])

>>> exp = torch.arange(1., 5.)
>>> base = 2
>>> torch.pow(base, exp)
tensor([  2.,   4.,   8.,  16.])

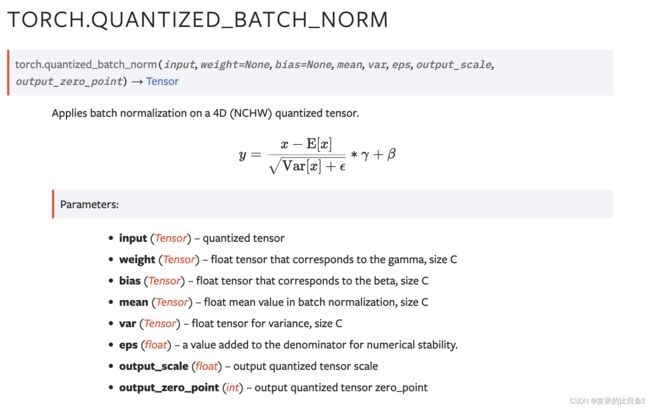
TORCH.QUANTIZED_BATCH_NORM

对 4D (NCHW) 量化张量应用批量归一化。

>>> qx = torch.quantize_per_tensor(torch.rand(2, 2, 2, 2), 1.5, 3, torch.quint8)
>>> torch.quantized_batch_norm(qx, torch.ones(2), torch.zeros(2), torch.rand(2), torch.rand(2), 0.00001, 0.2, 2)
tensor([[[[-0.2000, -0.2000],
      [ 1.6000, -0.2000]],

     [[-0.4000, -0.4000],
      [-0.4000,  0.6000]]],


    [[[-0.2000, -0.2000],
      [-0.2000, -0.2000]],

     [[ 0.6000, -0.4000],
      [ 0.6000, -0.4000]]]], size=(2, 2, 2, 2), dtype=torch.quint8,
   quantization_scheme=torch.per_tensor_affine, scale=0.2, zero_point=2)

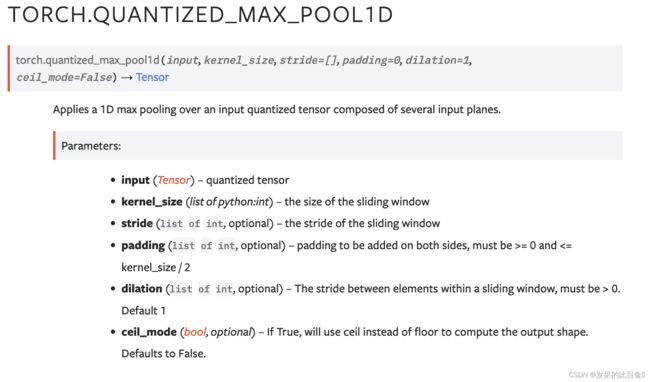
TORCH.QUANTIZED_MAX_POOL1D

在由多个输入平面组成的输入量化张量上应用一维最大池化。

>>> qx = torch.quantize_per_tensor(torch.rand(2, 2), 1.5, 3, torch.quint8)
>>> torch.quantized_max_pool1d(qx, [2])
tensor([[0.0000],
        [1.5000]], size=(2, 1), dtype=torch.quint8,
    quantization_scheme=torch.per_tensor_affine, scale=1.5, zero_point=3)

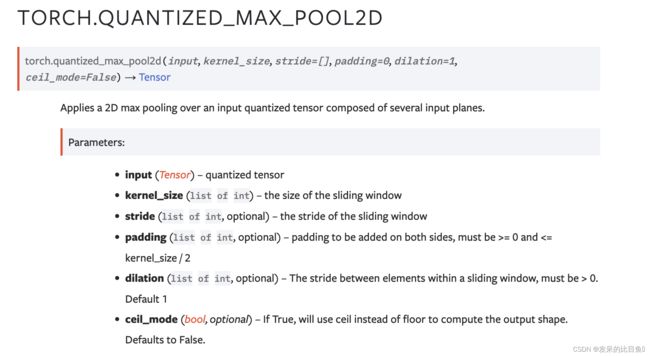
TORCH.QUANTIZED_MAX_POOL2D

在由多个输入平面组成的输入量化张量上应用 2D 最大池化。

>>> qx = torch.quantize_per_tensor(torch.rand(2, 2, 2, 2), 1.5, 3, torch.quint8)
>>> torch.quantized_max_pool2d(qx, [2,2])
tensor([[[[1.5000]],
        [[1.5000]]],
        [[[0.0000]],
        [[0.0000]]]], size=(2, 2, 1, 1), dtype=torch.quint8,
    quantization_scheme=torch.per_tensor_affine, scale=1.5, zero_point=3)

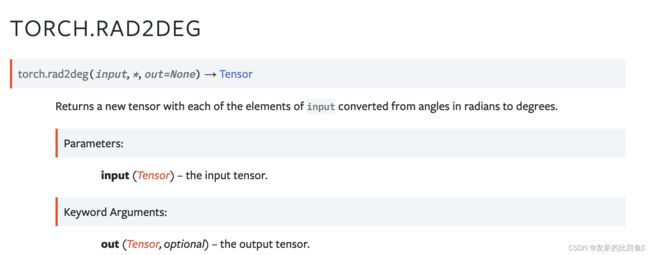
TORCH.RAD2DEG

返回一个新的张量，其中输入的每个元素都从以弧度为单位的角度转换为度数。

>>> a = torch.tensor([[3.142, -3.142], [6.283, -6.283], [1.570, -1.570]])
>>> torch.rad2deg(a)
tensor([[ 180.0233, -180.0233],
        [ 359.9894, -359.9894],
        [  89.9544,  -89.9544]])

TORCH.REAL

返回一个包含自张量实数值的新张量。返回的张量和 self 共享相同的底层存储。

>>> x=torch.randn(4, dtype=torch.cfloat)
>>> x
tensor([(0.3100+0.3553j), (-0.5445-0.7896j), (-1.6492-0.0633j), (-0.0638-0.8119j)])
>>> x.real
tensor([ 0.3100, -0.5445, -1.6492, -0.0638])

TORCH.RECIPROCAL

返回一个新的张量与输入元素的倒数

>>> a = torch.randn(4)
>>> a
tensor([-0.4595, -2.1219, -1.4314,  0.7298])
>>> torch.reciprocal(a)
tensor([-2.1763, -0.4713, -0.6986,  1.3702])

TORCH.REMAINDER

结果与除数other同号且绝对值小于other。

>>> torch.remainder(torch.tensor([-3., -2, -1, 1, 2, 3]), 2)
tensor([ 1.,  0.,  1.,  1.,  0.,  1.])
>>> torch.remainder(torch.tensor([1, 2, 3, 4, 5]), -1.5)
tensor([ -0.5000, -1.0000,  0.0000, -0.5000, -1.0000 ])

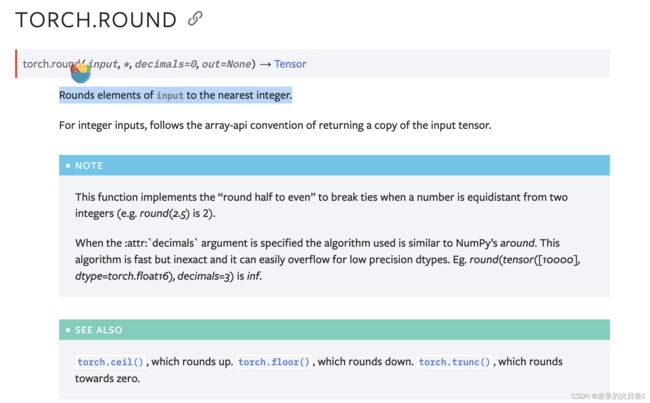
TORCH.ROUND

将输入的元素四舍五入为最接近的整数。

>>> torch.round(torch.tensor((4.7, -2.3, 9.1, -7.7)))
tensor([ 5.,  -2.,  9., -8.])

>>> # Values equidistant from two integers are rounded towards the
>>> #   the nearest even value (zero is treated as even)
>>> torch.round(torch.tensor([-0.5, 0.5, 1.5, 2.5]))
tensor([-0., 0., 2., 2.])

>>> # A positive decimals argument rounds to the to that decimal place
>>> torch.round(torch.tensor([0.1234567]), decimals=3)
tensor([0.1230])

>>> # A negative decimals argument rounds to the left of the decimal
>>> torch.round(torch.tensor([1200.1234567]), decimals=-3)
tensor([1000.])

TORCH.RSQRT

返回一个新的张量，它是输入的每个元素的平方根的倒数。

>>> a = torch.randn(4)
>>> a
tensor([-0.0370,  0.2970,  1.5420, -0.9105])
>>> torch.rsqrt(a)
tensor([    nan,  1.8351,  0.8053,     nan])

TORCH.SIGMOID

torch.special.expit().别名

>>> t = torch.randn(4)
>>> t
tensor([ 0.9213,  1.0887, -0.8858, -1.7683])
>>> torch.special.expit(t)
tensor([ 0.7153,  0.7481,  0.2920,  0.1458])

TORCH.SIGN

返回一个带有输入元素符号的新张量。

>>> a = torch.tensor([0.7, -1.2, 0., 2.3])
>>> a
tensor([ 0.7000, -1.2000,  0.0000,  2.3000])
>>> torch.sign(a)
tensor([ 1., -1.,  0.,  1.])

TORCH.SGN

此函数是 torch.sign() 对复杂张量的扩展。它计算一个新的张量，其元素与输入的对应元素具有相同的角度，对于复数张量，绝对值（即幅度）为 1，对于非复数张量，它等效于 torch.sign()。

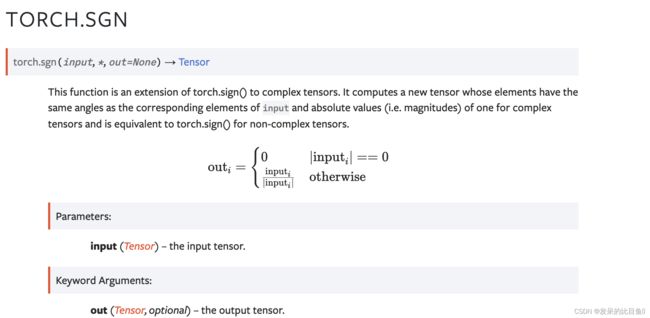
>>> t = torch.tensor([3+4j, 7-24j, 0, 1+2j])
>>> t.sgn()
tensor([0.6000+0.8000j, 0.2800-0.9600j, 0.0000+0.0000j, 0.4472+0.8944j])

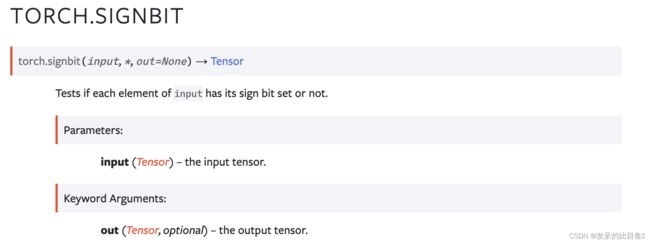
TORCH.SIGNBIT

测试输入的每个元素是否设置了符号位。

>>> a = torch.tensor([0.7, -1.2, 0., 2.3])
>>> torch.signbit(a)
tensor([ False, True,  False,  False])
>>> a = torch.tensor([-0.0, 0.0])
>>> torch.signbit(a)
tensor([ True,  False])

TORCH.SIN

>>> a = torch.randn(4)
>>> a
tensor([-0.5461,  0.1347, -2.7266, -0.2746])
>>> torch.sin(a)
tensor([-0.5194,  0.1343, -0.4032, -0.2711])

TORCH.SINC

torch.special.sinc().别名

>>> t = torch.randn(4)
>>> t
tensor([ 0.2252, -0.2948,  1.0267, -1.1566])
>>> torch.special.sinc(t)
tensor([ 0.9186,  0.8631, -0.0259, -0.1300])

TORCH.SINH

>>> a = torch.randn(4)
>>> a
tensor([ 0.5380, -0.8632, -0.1265,  0.9399])
>>> torch.sinh(a)
tensor([ 0.5644, -0.9744, -0.1268,  1.0845])

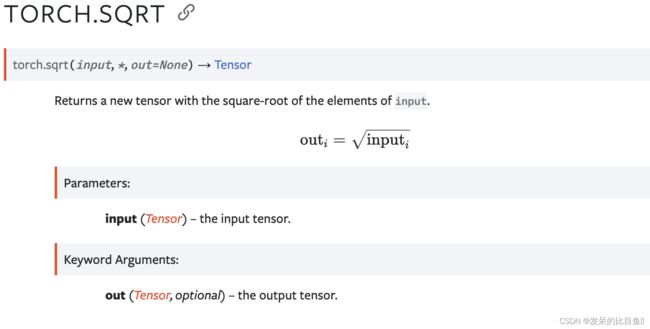
TORCH.SQRT

>>> a = torch.randn(4)
>>> a
tensor([-2.0755,  1.0226,  0.0831,  0.4806])
>>> torch.sqrt(a)
tensor([    nan,  1.0112,  0.2883,  0.6933])

TORCH.SQUARE

返回一个新的张量，其中包含输入元素的平方。

>>> a = torch.randn(4)
>>> a
tensor([-2.0755,  1.0226,  0.0831,  0.4806])
>>> torch.square(a)
tensor([ 4.3077,  1.0457,  0.0069,  0.2310])

TORCH.SUB

>>> a = torch.tensor((1, 2))
>>> b = torch.tensor((0, 1))
>>> torch.sub(a, b, alpha=2)
tensor([1, 0])

TORCH.SUBTRACT

TORCH.TAN

>>> a = torch.randn(4)
>>> a
tensor([-1.2027, -1.7687,  0.4412, -1.3856])
>>> torch.tan(a)
tensor([-2.5930,  4.9859,  0.4722, -5.3366])

TORCH.TANH

>>> a = torch.randn(4)
>>> a
tensor([ 0.8986, -0.7279,  1.1745,  0.2611])
>>> torch.tanh(a)
tensor([ 0.7156, -0.6218,  0.8257,  0.2553])

TORCH.TRUE_DIVIDE

torch.div()关于 rounding_mode=None的别名

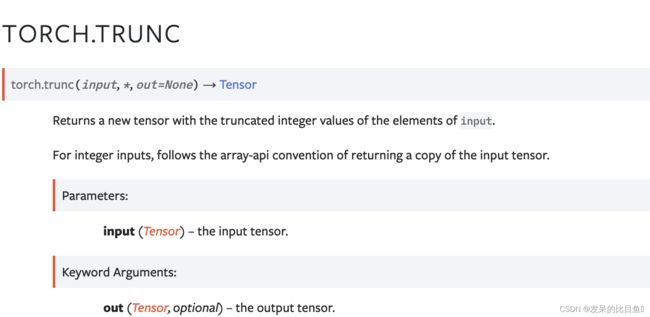
TORCH.TRUNC

返回一个新的张量，其中包含输入元素的截断整数值。

对于整数输入，遵循返回输入张量副本的 array-api 约定。

>>> a = torch.randn(4)
>>> a
tensor([ 3.4742,  0.5466, -0.8008, -0.9079])
>>> torch.trunc(a)
tensor([ 3.,  0., -0., -0.])

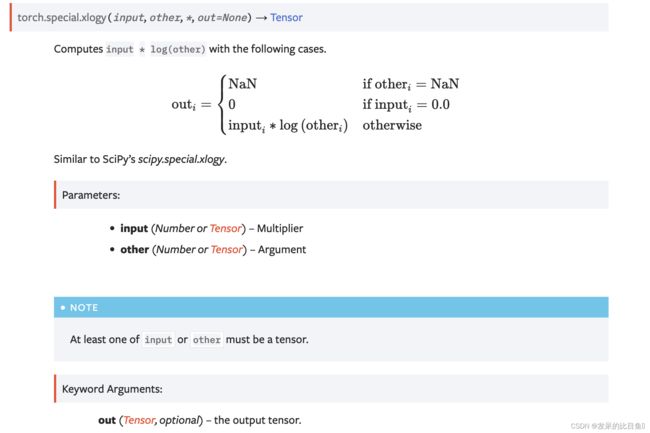
TORCH.XLOGY

torch.special.xlogy(). 别名

>>> x = torch.zeros(5,)
>>> y = torch.tensor([-1, 0, 1, float('inf'), float('nan')])
>>> torch.special.xlogy(x, y)
tensor([0., 0., 0., 0., nan])
>>> x = torch.tensor([1, 2, 3])
>>> y = torch.tensor([3, 2, 1])
>>> torch.special.xlogy(x, y)
tensor([1.0986, 1.3863, 0.0000])
>>> torch.special.xlogy(x, 4)
tensor([1.3863, 2.7726, 4.1589])
>>> torch.special.xlogy(2, y)
tensor([2.1972, 1.3863, 0.0000])

你可能感兴趣的:(PyTorch框架,pytorch,深度学习,python)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
一文掌握python面向对象魔术方法（二）程序员neil python python 开发语言
接上篇：一文掌握python面向对象魔术方法（一）-CSDN博客目录六、迭代和序列化：1、__iter__(self):定义迭代器，使得类可以被for循环迭代。2、__getitem__(self,key):定义索引操作，如obj[key]。3、__setitem__(self,key,value):定义赋值操作，如obj[key]=value。4、__delitem__(self,key):定义
一文掌握python常用的list（列表）操作程序员neil python python 开发语言
目录一、创建列表1.直接创建列表：2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素，索引从0开始：2.还可以使用切片操作访问列表的一部分：三、修改列表元素四、添加元素1.append()：在末尾添加元素2.insert()：在指定位置插入元素五、删除元素1.del：删除指定位置的元素2.remove()：删除指定值的第一个匹配项3.pop()：
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
python中的深拷贝与浅拷贝 anshejd70787 python
深拷贝和浅拷贝浅拷贝的时候，修改原来的对象，浅拷贝的对象不会发生改变。1、对象的赋值对象的赋值实际上是对象之间的引用：当创建一个对象，然后将这个对象赋值给另外一个变量的时候，python并没有拷贝这个对象，而只是拷贝了这个对象的引用。当对对象做赋值或者是参数传递或者作为返回值的时候，总是传递原始对象的引用，而不是一个副本。如下所示：>>>aList=["kel","abc",123]>>>bLis
[黑洞与暗粒子]没有光的世界 comsci
无论是相对论还是其它现代物理学,都显然有个缺陷,那就是必须有光才能够计算但是,我相信,在我们的世界和宇宙平面中,肯定存在没有光的世界.... 那么,在没有光的世界,光子和其它粒子的规律无法被应用和考察,那么以光速为核心的 &nbs
jQuery Lazy Load 图片延迟加载 aijuans jquery
基于 jQuery 的图片延迟加载插件，在用户滚动页面到图片之后才进行加载。对于有较多的图片的网页，使用图片延迟加载，能有效的提高页面加载速度。版本： jQuery v1.4.4+ jQuery Lazy Load v1.7.2 注意事项：需要真正实现图片延迟加载，必须将真实图片地址写在 data-original 属性中。若 src
使用Jodd的优点 Kai_Ge jodd
1. 简化和统一 controller ，抛弃 extends SimpleFormController ，统一使用 implements Controller 的方式。 2. 简化 JSP 页面的 bind, 不需要一个字段一个字段的绑定。 3. 对 bean 没有任何要求，可以使用任意的 bean 做为 formBean。使用方法简介
jpa Query转hibernate Query 120153216 Hibernate
public List<Map> getMapList(String hql, Map map) { org.hibernate.Query jpaQuery = entityManager.createQuery(hql); if (null != map) { for (String parameter : map.keySet()) { jp
Django_Python3添加MySQL/MariaDB支持 2002wmj mariaDB
现状首先，[email protected] 中默认的引擎为 django.db.backends.mysql 。但是在Python3中如果这样写的话，会发现 django.db.backends.mysql 依赖 MySQLdb[5] ，而 MySQLdb 又不兼容 Python3 于是要找一种新的方式来继续使用MySQL。 MySQL官方的方案首先据MySQL文档[3]说，自从MySQL
在SQLSERVER中查找消耗IO最多的SQL 357029540 SQL Server
返回做IO数目最多的50条语句以及它们的执行计划。 select top 50 (total_logical_reads/execution_count) as avg_logical_reads, (total_logical_writes/execution_count) as avg_logical_writes, (tot
spring UnChecked 异常官方定义！ 7454103 spring
如果你接触过spring的事物管理！那么你必须明白 spring的非捕获异常！即 unchecked 异常！因为 spring 默认这类异常事物自动回滚！！ public static boolean isCheckedException(Throwable ex) { return !(ex instanceof RuntimeExcep
mongoDB 入门指南、示例 adminjun java mongodb 操作
一、准备工作 1、下载mongoDB 下载地址：http://www.mongodb.org/downloads 选择合适你的版本相关文档：http://www.mongodb.org/display/DOCS/Tutorial 2、安装mongoDB A、不解压模式：将下载下来的mongoDB-xxx.zip打开，找到bin目录，运行mongod.exe就可以启动服务，默
CUDA 5 Release Candidate Now Available aijuans CUDA
The CUDA 5 Release Candidate is now available at http://developer.nvidia.com/<wbr></wbr>cuda/cuda-pre-production. Now applicable to a broader set of algorithms, CUDA 5 has advanced fe
Essential Studio for WinRT网格控件测评 Axiba JavaScript html5
Essential Studio for WinRT界面控件包含了商业平板应用程序开发中所需的所有控件，如市场上运行速度最快的grid 和chart、地图、RDL报表查看器、丰富的文本查看器及图表等等。同时，该控件还包含了一组独特的库，用于从WinRT应用程序中生成Excel、Word以及PDF格式的文件。此文将对其另外一个强大的控件——网格控件进行专门的测评详述。网格控件功能 1、
java 获取windows系统安装的证书或证书链 bewithme windows
有时需要获取windows系统安装的证书或证书链，比如说你要通过证书来创建java的密钥库。有关证书链的解释可以查看此处。 public static void main(String[] args) { SunMSCAPI providerMSCAPI = new SunMSCAPI(); S
NoSQL数据库之Redis数据库管理(set类型和zset类型) bijian1013 redis 数据库 NoSQL
4.sets类型 Set是集合，它是string类型的无序集合。set是通过hash table实现的，添加、删除和查找的复杂度都是O(1)。对集合我们可以取并集、交集、差集。通过这些操作我们可以实现sns中的好友推荐和blog的tag功能。 sadd：向名称为key的set中添加元
异常捕获何时用Exception，何时用Throwable bingyingao
用Exception的情况 try { //可能发生空指针、数组溢出等异常 } catch (Exception e) {
【Kafka四】Kakfa伪分布式安装 bit1129 kafka
在http://bit1129.iteye.com/blog/2174791一文中，实现了单Kafka服务器的安装，在Kafka中，每个Kafka服务器称为一个broker。本文简单介绍下，在单机环境下Kafka的伪分布式安装和测试验证 1. 安装步骤 Kafka伪分布式安装的思路跟Zookeeper的伪分布式安装思路完全一样，不过比Zookeeper稍微简单些(不
Project Euler bookjovi haskell
Project Euler是个数学问题求解网站，网站设计的很有意思，有很多problem，在未提交正确答案前不能查看problem的overview，也不能查看关于problem的discussion thread，只能看到现在problem已经被多少人解决了，人数越多往往代表问题越容易。看看problem 1吧： Add all the natural num
Java-Collections Framework学习与总结-ArrayDeque BrokenDreams Collections
表、栈和队列是三种基本的数据结构，前面总结的ArrayList和LinkedList可以作为任意一种数据结构来使用，当然由于实现方式的不同，操作的效率也会不同。这篇要看一下java.util.ArrayDeque。从命名上看
读《研磨设计模式》-代码笔记-装饰模式-Decorator bylijinnan java 设计模式
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ import java.io.BufferedOutputStream; import java.io.DataOutputStream; import java.io.FileOutputStream; import java.io.Fi
Maven学习(一) chenyu19891124 Maven私服
学习一门技术和工具总得花费一段时间，5月底6月初自己学习了一些工具，maven+Hudson+nexus的搭建，对于maven以前只是听说，顺便再自己的电脑上搭建了一个maven环境，但是完全不了解maven这一强大的构建工具，还有ant也是一个构建工具，但ant就没有maven那么的简单方便，其实简单点说maven是一个运用命令行就能完成构建，测试，打包，发布一系列功
[原创]JWFD工作流引擎设计----节点匹配搜索算法(用于初步解决条件异步汇聚问题) 补充 comsci 算法工作 PHP 搜索引擎嵌入式
本文主要介绍在JWFD工作流引擎设计中遇到的一个实际问题的解决方案，请参考我的博文"带条件选择的并行汇聚路由问题"中图例A2描述的情况(http://comsci.iteye.com/blog/339756),我现在把我对图例A2的一个解决方案公布出来，请大家多指点节点匹配搜索算法(用于解决标准对称流程图条件汇聚点运行控制参数的算法) 需要解决的问题：已知分支
Linux中用shell获取昨天、明天或多天前的日期 daizj linux shell 上几年昨天获取上几个月
在Linux中可以通过date命令获取昨天、明天、上个月、下个月、上一年和下一年 # 获取昨天 date -d 'yesterday' # 或 date -d 'last day' # 获取明天 date -d 'tomorrow' # 或 date -d 'next day' # 获取上个月 date -d 'last month' #
我所理解的云计算 dongwei_6688 云计算
在刚开始接触到一个概念时，人们往往都会去探寻这个概念的含义，以达到对其有一个感性的认知，在Wikipedia上关于“云计算”是这么定义的，它说： Cloud computing is a phrase used to describe a variety of computing co
YII CMenu配置 dcj3sjt126com yii
Adding id and class names to CMenu We use the id and htmlOptions to accomplish this. Watch. //in your view $this->widget('zii.widgets.CMenu', array( 'id'=>'myMenu', 'items'=>$this-&g
设计模式之静态代理与动态代理 come_for_dream 设计模式
静态代理与动态代理代理模式是java开发中用到的相对比较多的设计模式，其中的思想就是主业务和相关业务分离。所谓的代理设计就是指由一个代理主题来操作真实主题，真实主题执行具体的业务操作，而代理主题负责其他相关业务的处理。比如我们在进行删除操作的时候需要检验一下用户是否登陆，我们可以删除看成主业务，而把检验用户是否登陆看成其相关业务
【转】理解Javascript 系列 gcc2ge JavaScript
理解Javascript_13_执行模型详解摘要: 在《理解Javascript_12_执行模型浅析》一文中,我们初步的了解了执行上下文与作用域的概念，那么这一篇将深入分析执行上下文的构建过程，了解执行上下文、函数对象、作用域三者之间的关系。函数执行环境简单的代码:当调用say方法时，第一步是创建其执行环境，在创建执行环境的过程中，会按照定义的先后顺序完成一系列操作:1.首先会创建一个
Subsets II hcx2013 set
Given a collection of integers that might contain duplicates, nums, return all possible subsets. Note: Elements in a subset must be in non-descending order. The solution set must not conta
Spring4.1新特性——Spring缓存框架增强 jinnianshilongnian spring4
目录 Spring4.1新特性——综述 Spring4.1新特性——Spring核心部分及其他 Spring4.1新特性——Spring缓存框架增强 Spring4.1新特性——异步调用和事件机制的异常处理 Spring4.1新特性——数据库集成测试脚本初始化 Spring4.1新特性——Spring MVC增强 Spring4.1新特性——页面自动化测试框架Spring MVC T
shell嵌套expect执行命令 liyonghui160com
一直都想把expect的操作写到bash脚本里,这样就不用我再写两个脚本来执行了,搞了一下午终于有点小成就,给大家看看吧. 系统:centos 5.x 1.先安装expect yum -y install expect 2.脚本内容: cat auto_svn.sh #!/bin/bash
Linux实用命令整理 pda158 linux
0. 基本命令　　linux 基本命令整理　　1. 压缩解压　　tar -zcvf a.tar.gz a #把a压缩成a.tar.gz 　　tar -zxvf a.tar.gz #把a.tar.gz解压成a 　　2. vim小结　　2.1 vim替换　　:m,ns/word_1/word_2/gc
独立开发人员通向成功的29个小贴士 shoothao 独立开发
概述：本文收集了关于独立开发人员通向成功需要注意的一些东西,对于具体的每个贴士的注解有兴趣的朋友可以查看下面标注的原文地址。明白你从事独立开发的原因和目的。保持坚持制定计划的好习惯。万事开头难，第一份订单是关键。培养多元化业务技能。提供卓越的服务和品质。谨小慎微。营销是必备技能。学会组织，有条理的工作才是最有效率的。 “独立
JAVA中堆栈和内存分配原理 uule java
1、栈、堆 1.寄存器：最快的存储区, 由编译器根据需求进行分配,我们在程序中无法控制.2. 栈：存放基本类型的变量数据和对象的引用，但对象本身不存放在栈中，而是存放在堆（new 出来的对象）或者常量池中（字符串常量对象存放在常量池中。）3. 堆：存放所有new出来的对象。4. 静态域：存放静态成员（static定义的）5. 常量池：存放字符串常量和基本类型常量（public static f