easy 二叉树的中序遍历 递归 栈 Morris 莫里斯遍历 stack容器

前序遍历,出栈顺序:根左右; 入栈顺序:右左根
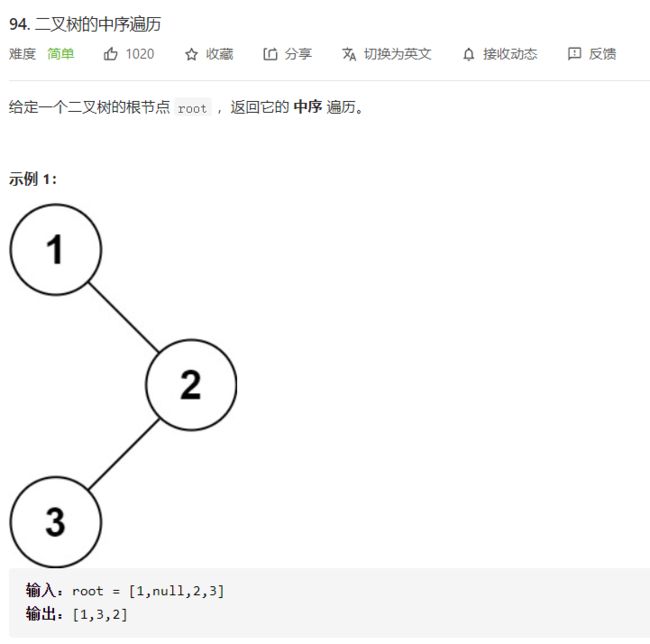
中序遍历,出栈顺序:左根右; 入栈顺序:右根左
后序遍历,出栈顺序:左右根; 入栈顺序:根右左
递归:
c++:
leetcode插入自己的函数
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
// 自己的函数
void inorder(TreeNode* root, vector<int>& res){ // 传入向量指针 &res
if(root==NULL){ // 递归终止的条件为碰到空节点
return;
}
inorder(root->left,res);
res.push_back(root->val);
inorder(root->right,res);
}
// 主函数
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
inorder(root,res); // 子函数传入参数根节点
return res;
}
};
python:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
res=[]
def inorder(root): # 先写函数
if not root:
return
inorder(root.left)
res.append(root.val)
inorder(root.right)
inorder(root) # 调用函数
return res
栈(迭代):
从根节点开始找二叉树的最左节点,将走过的节点保存在一个栈中,找到最左节点后访问,对于每个节点来说,它都是以自己为根的子树的根节点,访问完之后就可以转到右节点上:
c++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
stack<TreeNode*>stk; //stack容器 存放指向TreeNode的指针
while(root!=nullptr || !stk.empty()){ // 节点为空且栈空,则已访问完最右节点,
while(root != nullptr){ // 找到最左节点
stk.push(root); // 将遍历到的左节点放到栈中
root = root->left; // 遍历下一个左节点
}
root = stk.top(); // 开始回溯,栈顶为第一个访问的根
res.push_back(root->val); // 此时栈顶为最左节点(该根下面没有左节点),输出该根
root = root->right; // 访问该根右节点
stk.pop(); // 访问完毕,出栈
}
return res;
}
};
python:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
if not root:
return []
res= []
stack = []
while root or stack: # 栈不为空就循环
while root: # 找到最左节点
stack.append(root)
root = root.left
# 开始回溯
root = stack[-1] # (遍历到最左节点时,while中root = root.left = nullptr)所以root从stack取
res.append(root.val) # 输出该根
root = root.right # 访问根右节点
stack.pop() # 访问完毕,出栈
return res
Morris 莫里斯遍历
动画演示
根有左树,就把根连同右树放到左树最右节点的右节点。
移动后把根,更新为原根的左节点
循环,根有左树,就把根…
根没有左树了,就开始访问根,并从根遍历根的右节点。每次遍历到新根有开始检查有没有左树
python:
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def inorderTraversal(self, root: TreeNode) -> List[int]:
res = []
pre = None
# 如果左节点不为空,就将当前节点连带右子树全部挂到左节点的最右子树下面
while root:
if root.left: # 根左树
pre = root.left
while pre.right: # 找到根左树的最右节点
pre = pre.right
pre.right = root # 此时最右节点下面已无右节点 pre.right = null,将根root挂到最右节点下面右节点
tmp = root # 暂存原根root
root = root.left # 新根为原根左节点(原根左树第一个节点)
tmp.left = None # 原根与左树脱离,原根及其右树全部移到原根左树最右节点的右节点
else: # 左树为空,打印该根,并向右遍历
res.append(root.val)
root = root.right
return res
c++:
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> res;
TreeNode *pre = nullptr;
TreeNode *tmp = nullptr;
while(root){
if (root->left){
pre = root->left;
while(pre->right){
pre = pre->right;
}
pre->right = root; // 当前节点连带右子树全部挂到,左节点的最右子树下面
tmp = root;
root = root->left; // 新根为原根左节点(原根左树第一个节点)
tmp->left = nullptr;
}else{
res.push_back(root->val);
root = root->right;
}
}
return res;
}
};




