PageRank算法原理及代码
本文内容出自帅器学习的课程内容,讲得原理清晰,概念深入,链接: PANKRANK算法视频
另有一篇知乎文章,PAGERANK讲得系统透彻,链接在此:关键词提取和摘要算法TextRank详解与实战
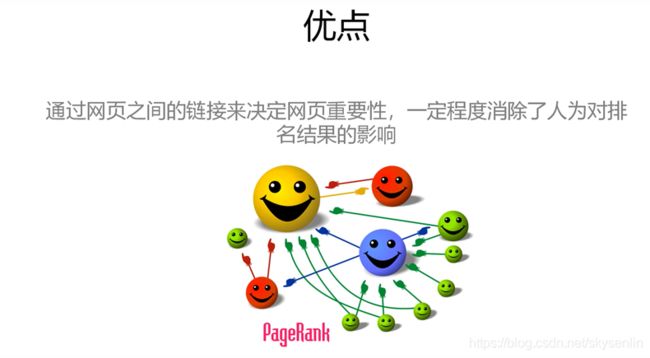
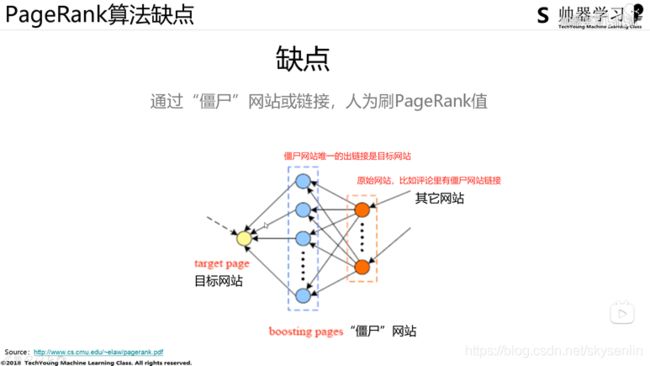
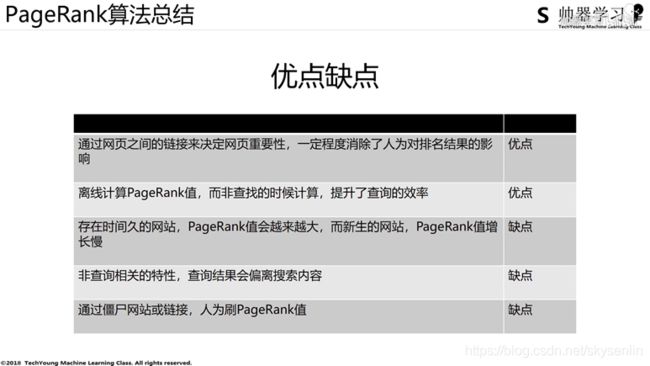
PAGERANK算法是一种网页排名算法,其基本思路有两条:
- 链接数量。一个网页被越多的其他网页链接,说明这个网页很重要。
- 链接质量。一个网页被一个越高权值的网页链接,也能表明这个网页越重要。
1、课程导论
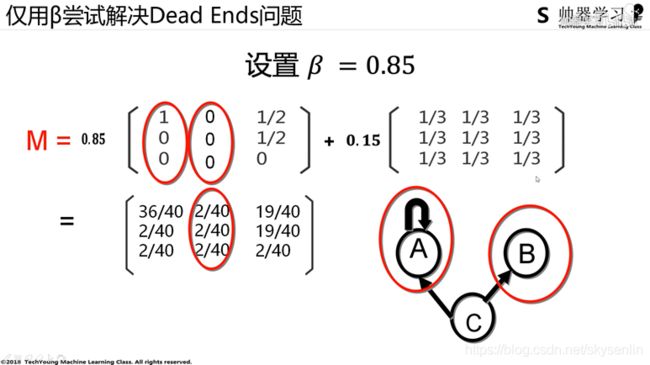
| 由A出链到其他节点,即由A可以发射到B C | ||||
| A | B | C | D | |
| A | 0 | 0 | 0 | 1 |
| B | 1 | 0 | 0 | 0 |
| C | 1 | 1 | 1 | 0 |
| D | 0 | 1 | 1 | 0 |
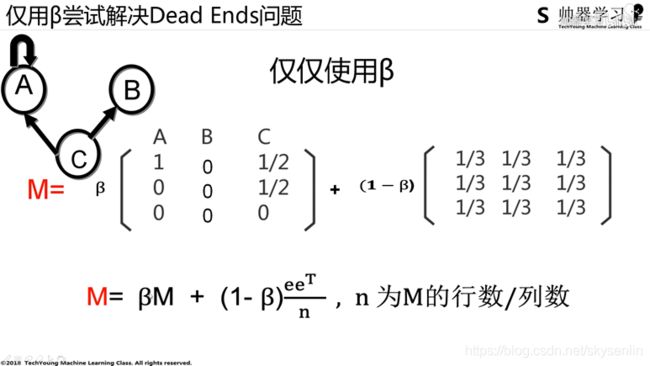
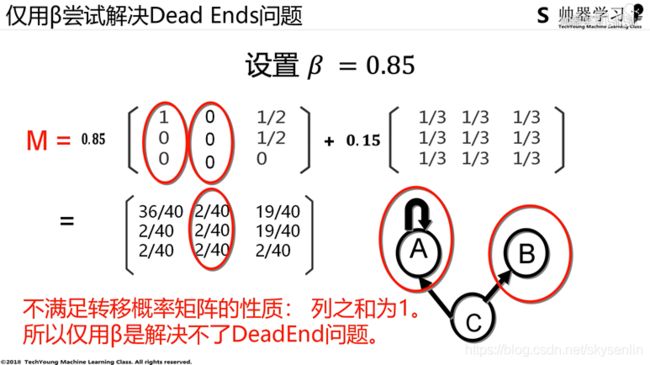
经过反复研究,这个最终公式是有问题的,应该改为
2、代码实践
俗话说实践出真知,听课听懂了,结果实践的时候折腾了一天才弄明白,因为计算pagerank目前已经有成熟的算法,我根据networkx和pygraph现成的算法去验证自己写的是否有问题。
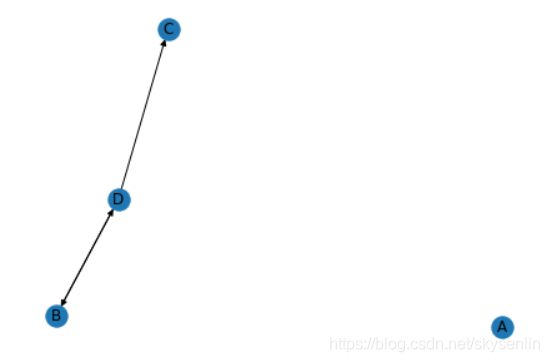
问题,目前有4个网页A B C D
入链和出链关系如下图,那么这4个网页的pagerank是多少呢?
2.1 自写算法
import numpy as np
p = 0.85 #引入浏览当前网页的概率为p,假设p=0.8
a = np.array([[1,0,0,0],
[0,0,0,1],
[0,0,0,1],
[0,1,0,0]],dtype = float) #dtype指定为float
length=a.shape[1] #网页数量
#构造转移矩阵
b = np.transpose(a) #b为a的转置矩阵
m = np.zeros((a.shape),dtype = float)
for i in range(a.shape[0]):
for j in range(a.shape[1]):
#如果一个节点没有任何出链,Dead Ends
if b[j].sum()==0:
b[j]=b[j]+np.array([1/length]*length)
m[i][j] = a[i][j] / (b[j].sum()) #完成初始化分配
#pr值得初始化
v = np.zeros((m.shape[0],1),dtype = float) #构造一个存放pr值得矩阵
for i in range(m.shape[0]):
v[i] = float(1)/m.shape[0]
count=0
ee=np.array([[1/length]*length]).reshape(length,-1)
# 循环100次计算pageRank值
for i in range(100):
# 解决spider traps问题,spider traps会导致网站权重向一个节点偏移,将转移矩阵加上打开其他网页的概率1-p
v = p*np.dot(m,v) + (1-p)*ee
count+=1
print("第{}次迭代".format(count))
#pageRank值
print(v)2.2 networkx算法
import networkx as nx
import matplotlib.pyplot as plt
# 创建有向图
G = nx.DiGraph()
# 有向图之间边的关系
edges = [("A", "A"), ("B", "D"), ("D", "B"), ("D", "C")]
for edge in edges:
G.add_edge(edge[0], edge[1])
nx.draw(G,with_labels=True)
plt.show()
pagerank_list = nx.pagerank(G, alpha=0.85)
print("pagerank值是:\n", pagerank_list)2.3 pygraph算法
from pygraph.classes.digraph import digraph
dg = digraph()
dg.add_nodes(["A", "B", "C", "D"])
dg.add_edge(("A", "A"))
dg.add_edge(("B", "D"))
dg.add_edge(("D", "B"))
dg.add_edge(("D", "C"))
damping_factor = 0.85 # 阻尼系数,即α
max_iterations = 100 # 最大迭代次数
min_delta = 0.00001 # 确定迭代是否结束的参数,即ϵ
graph = dg
for node in graph.nodes():
if len(graph.neighbors(node)) == 0:
for node2 in graph.nodes():
print("node:",node,"node2:",node2)
digraph.add_edge(graph, (node, node2))
print(graph)
print("-"*5)
print("="*30)
nodes = graph.nodes()
graph_size = len(nodes)
page_rank = dict.fromkeys(nodes, 1.0 / graph_size) # 给每个节点赋予初始的PR值
damping_value = (1.0 - damping_factor) / graph_size # 公式中的(1−α)/N部分
flag = False
for i in range(max_iterations):
change = 0
for node in nodes:
rank = 0
for incident_page in graph.incidents(node): # 遍历所有“入射”的页面
rank += damping_factor * (page_rank[incident_page] / len(graph.neighbors(incident_page)))
rank += damping_value
change += abs(page_rank[node] - rank) # 绝对值
page_rank[node] = rank
if change < min_delta:
flag = True
break
if flag:
print("finished in %s iterations!" % node)
else:
print("finished out of 100 iterations!")
print(page_rank)
3、对比
自写算法结果:
[[0.47534884]
[0.15906977]
[0.15906977]
[0.20651163]]
nx算法结果:
{'A': 0.47534154833093023, 'B': 0.15907194271825495, 'C': 0.15907194271825495, 'D': 0.20651456623255982}
pygraph结果:
{'A': 0.47529602196443255, 'B': 0.1590697675524163, 'C': 0.1590697675524163, 'D': 0.20651162802444234}自此,我们的理论和实践初级入门就可以了!
4、应用
pagerank既可以用在网页质量的排名,也可以应用到网状节点类的各种问题,比如社交网络、各城市资本流向,以及改进后的TextRank,本文应用从希拉里用私人邮箱处理公务成为丑闻 事件为切入点,理解利用pagerank计算节点度量性。
# -*- coding: utf-8 -*-
# 用 PageRank 挖掘希拉里邮件中的重要任务关系
import pandas as pd
import networkx as nx
import numpy as np
from collections import defaultdict
import matplotlib.pyplot as plt
import os
os.chdir("D:/pagerank/data/")
# 数据加载
emails = pd.read_csv("Emails.csv")
# 读取别名文件
file = pd.read_csv("Aliases.csv")
aliases = {}
for index, row in file.iterrows():
aliases[row['Alias']] = row['PersonId']
# 读取人名文件
file = pd.read_csv("Persons.csv")
persons = {}
for index, row in file.iterrows():
persons[row['Id']] = row['Name']
# 针对别名进行转换
def unify_name(name):
# 姓名统一小写
name = str(name).lower()
# 去掉, 和 @后面的内容
name = name.replace(",","").split("@")[0]
# 别名转换
if name in aliases.keys():
return persons[aliases[name]]
return name
# 画网络图
def show_graph(graph, layout='spring_layout'):
# 使用 Spring Layout 布局,类似中心放射状
if layout == 'circular_layout':
positions=nx.circular_layout(graph)
else:
positions=nx.spring_layout(graph)
# 设置网络图中的节点大小,大小与 pagerank 值相关,因为 pagerank 值很小所以需要 *20000
nodesize = [x['pagerank']*20000 for v,x in graph.nodes(data=True)]
# 设置网络图中的边长度
edgesize = [np.sqrt(e[2]['weight']) for e in graph.edges(data=True)]
# 绘制节点
nx.draw_networkx_nodes(graph, positions, node_size=nodesize, alpha=0.4)
# 绘制边
nx.draw_networkx_edges(graph, positions, edge_size=edgesize, alpha=0.2)
# 绘制节点的 label
nx.draw_networkx_labels(graph, positions, font_size=10)
# 输出希拉里邮件中的所有人物关系图
plt.show()
# 将寄件人和收件人的姓名进行规范化
emails.MetadataFrom = emails.MetadataFrom.apply(unify_name)
emails.MetadataTo = emails.MetadataTo.apply(unify_name)
# 设置遍的权重等于发邮件的次数
edges_weights_temp = defaultdict(list) #defaultdict当字典里的Key不存在时,返回默认值[]
for row in zip(emails.MetadataFrom, emails.MetadataTo, emails.RawText):
temp = (row[0], row[1])
if temp not in edges_weights_temp:
edges_weights_temp[temp] = 1
else:
edges_weights_temp[temp] = edges_weights_temp[temp] + 1
# 转化格式 (from, to), weight => from, to, weight
edges_weights = [(key[0], key[1], val) for key, val in edges_weights_temp.items()]
# 创建一个有向图
graph = nx.DiGraph()
# 设置有向图中的路径及权重 (from, to, weight) add_weighted_edges_fromu、v、w 分别代表起点、终点和权重。
graph.add_weighted_edges_from(edges_weights)
# 计算每个节点(人)的 PR 值,并作为节点的 pagerank 属性
pagerank = nx.pagerank(graph)
# 将 pagerank 数值作为节点的属性
nx.set_node_attributes(graph, name = 'pagerank', values=pagerank)
# 画网络图
show_graph(graph)
# 将完整的图谱进行精简
# 设置 PR 值的阈值,筛选大于阈值的重要核心节点
pagerank_threshold = 0.005
# 复制一份计算好的网络图
small_graph = graph.copy()
# 剪掉 PR 值小于 pagerank_threshold 的节点
for n, p_rank in graph.nodes(data=True):
if p_rank['pagerank'] < pagerank_threshold:
small_graph.remove_node(n)
# 画网络图,采用circular_layout布局让筛选出来的点组成一个圆
show_graph(small_graph, 'circular_layout')
参考链接
PageRank算法与TextRank算法详解:点此链接
希拉里原始数据:点此链接
TextRank算法的基本原理及textrank4zh使用实例:点此链接