时序图文献精读——6.2019-ICLR-DYREP: LEARNING REPRESENTATIONS OVER DYNAMIC GRAPHS

DYREP: LEARNING REPRESENTATIONS OVER DYNAMIC GRAPHS

Abstract

在动态图的学习过程中出现了两个基本问题： (i)如何优雅地在图上建模动态过程？（ii）如何利用这样的模型来有效地将不断发展的图信息编码为低维表示？

我们提出了一个双时间尺度的深时间点过程模型，以捕获观测过程的交错动态。该模型被时间注意表示网络进一步参数化，该网络将时间演化的结构信息编码为节点表示，进而驱动观察到的图动力学的非线性演化。我们的统一框架是使用一个有效的无监督程序进行训练的，并具有泛化不可见节点的能力。

1.Introduction

我们关注动态图表示学习的两个相关问题：
(i)什么可以作为图形上的动态过程的优雅模型？
我们观察到大多数现实世界的图至少有两个在不同时间尺度上演化的不同的动态过程——拓扑进化：节点和边的数量预计会随着时间的推移而增长（或缩小），导致图中的结构变化；节点交互：与节点之间的活动可能有也可能没有结构连接的节点。对这些非线性演化的动态过程之间的交错依赖关系进行建模，是推进动态图的形式化模型的关键下一步
(ii)如何利用这样的模型来学习动态节点表示，从而能够有效地捕获随时间变化的图信息？
在这个方向上的现有技术可以分为两种方法：a)离散时间方法，将动态图的演变观察为静态图快照的集合。这些方法倾向于保存（编码）非常有限的结构信息，并在非常粗糙的级别上捕获时间信息，这导致快照之间的信息丢失和缺乏捕获细粒度时间动态的能力。这种方法中的另一个挑战是选择适当的聚合粒度，这经常被错误地指定。 b)连续时间方法，其中进化在更细的时间粒度上建模，以解决上述挑战。虽然现有的方法已被证明在特定环境下非常有效，但它们要么以解耦的方式建模简单的结构和复杂的时间属性，要么使用简单的时间模型。

有效学习这种动态系统的一个重要要求是在不同尺度上表达动态过程的能力。我们提出，任何动态图都必须最小限度地表示为在不同时间尺度上演化的两个基本过程的结果：
关联过程（网络的动态），带来图结构的变化，导致节点之间长期的信息交换；通信过程（网络上的动态），与节点之间的活动（不一定是连接的）节点有关，从而导致它们之间的临时信息流动。

我们假设学习节点表示的目标是建模一个潜在的中介过程，连接了上述两个观察到的过程，这样学习表示驱动这两个过程的复杂时间动态，这些过程随后导致节点表示的非线性演化。此外，在图中传播的信息受节点通信和关联历史的时间动态控制。我们将这种现象称为通过中介的进化，并在图1中以图形方式说明它。

在这项工作中，我们提出了一种新的动态图表示学习框架，DyRep，通过上述表达的潜在中介过程来建模两个观察过程的交错演化，并随着时间的推移有效地学习更丰富的节点表示。我们的框架随着时间的推移以关联和通信事件的形式摄取动态图信息，并在这些事件中出现时更新节点表示。最后，我们通过设计一种新的时间注意机制，将框架的结构和时间成分耦合，利用学习的强度函数诱导邻域节点上的时间注意。这允许捕获高度交错和非线性的动态控制节点表示。我们设计了一个有效的无监督训练程序的端到端训练我们的框架。
在动态链路预测和时间预测的任务中，我们展示了在两个真实世界的动态图上比最先进的代表性基线的一致和显著的改进。我们通过嵌入可视化和消融研究，进一步提出了广泛的定性分析，以识别我们的框架的有效性。

2.BACKGROUND AND PRELIMINARIES

2.1.RELATED WORK

这部分作者介绍了有关动态图节点表示的相关工作，感兴趣可以查看原文献。

2.2.TEMPORAL POINT PROCESSES

随机点过程是随机过程，其实现包括时间离散事件t1，t2，…A 时间点过程就是这样一个随机过程，可以等价地表示为计数过程N (t)，它包含到t之前的事件数量。表征时间点过程的常见方法是通过条件强度函数λ(t)，这是一个给定之前事件的事件发生率的随机模型。

强度λ(t)通常被设计用来捕捉感兴趣的现象——常见形式包括泊松过程、霍克斯过程

2.3.NOTATIONS AND DYNAMIC GRAPH SETTING

Notations 设Gt =（Vt，Et）表示t时刻的图G，其中Vt是节点的集，Et是Gt中的边的集，这些边是无向的

Event Observation 通信和关联过程都是通过在图G上的节点之间在一个时间窗口[t0，T]上观察到的二元事件的形式来实现的，并按时间排序。我们对e =（u，v，t，k）时刻t形式的任何类型的事件使用下面的规范元组表示，其中u，v是所涉及的在一个事件中的两个节点。t表示事件发生的时间。我们使用k∈{0,1}，我们使用k = 0表示来自拓扑演化过程（关联）的事件，并使用k = 1表示来自节点交互过程（通信）的事件。我们将窗口[0，T]中按时间排序的P观测事件的完整集合表示为O = {(u, v, t, k)p} P p=1,0 ≤ tp ≤ T

Node Representation 设zv∈Rd表示节点v的d维表示。随着表示随着时间的推移，我们将它们限定为时间的函数： z v (t)——节点v的表示在时间t时涉及v的事件后被更新。我们使用zv（t¯）来实现在t之前最近更新的节点v的嵌入。

Dynamic Graph Setting 设Gt0 =（Vt0，Et0）为t0时刻一个图的初始快照。请注意，Gt0可能是空的，也可能包含一个初始结构（关联边），但它将不会有任何通信历史记录。我们的框架观察图的演化作为一个事件流的O，因此任何新的节点将始终被观察为这样一个事件的一部分。这将导致对数据中可用的节点进行自然排序。由于我们的方法是归纳的，我们从不学习特定于节点的表示，而是学习函数来计算节点表示。在这项工作中，我们只支持网络的增长，即我们只建模节点和结构边的添加，并将删除作为未来的工作。

3.PROPOSED METHOD: DYREP

DyRep的关键思想是建立一个统一的体系结构，可以摄取图上的演化信息，并通过第1节中描述的中介现象有效地建模演化。为此，我们设计了一个双时间尺度的观测过程时间点过程模型，并利用归纳表示网络对其进行参数化，该网络随后对学习节点表示的潜在中介过程进行建模。

我们的框架背后的基本原理是，观察到的事件集是控制图的拓扑结构变化和图中节点之间的相互作用的非线性动态过程的实现。

3.1. MODELING TWO-TIME SCALE OBSERVED GRAPH DYNAMICS

给定一个观察到的事件p =（u，v，t，k），我们使用条件强度函数λ u，v k (t)定义了一个时间点过程的连续时间深度模型，该函数模拟了节点在t时u和v之间的事件p的发生：

其中，t¯表示当前事件之前的时间点。内部函数gk（t¯）计算两个最近更新的节点zu（t¯）和zv（t¯）的表示形式的兼容性:

该网络参数化了点过程模型的强度函数，作为一个统一的因素。请注意，动态并不是相互依赖的两个简单的点过程，而是通过中介过程和在嵌入空间中相互关联的。
因此，采用一种精心策划的注意力机制来了解过去如何驱动未来。

外部函数fk的选择需要考虑到两个关键的标准：
1)的强度必须为正的。
2)如前所述，沟通和联想过程在不同的时间尺度上进化

为了解释这一点，我们使用了一个由动态参数ψk参数化的软加函数的修改版本来捕获这种时间尺度依赖性：

例子中的x=g（t¯）和ψk（> 0）是作为训练的一部分学习到的标量时间尺度参数

3.2.LEARNING LATENT MEDIATION PROCESS VIA TEMPORALLY ATTENTIVE REPRESENTATION NETWORK

我们建立了一个深度循环架构，它参数化了等式中的**强度函数(1)**并学习函数来计算节点表示。具体来说，在一个事件发生后，需要更新这两个参与节点的表示，以根据以下原则捕获所观察到的事件的影响：

Self-Propagation
Exogenous Drive
Localized Embedding Propagation

考虑节点u和节点v在t时刻参与任何类型的事件。设Nu和Nv分别表示节点u和节点v的邻域。我们在这里讨论两个关键点： 1)节点u作为将信息从Nu传递到节点v的桥梁，因此v通过u以聚合的形式接收信息。2)当u的每个邻居将其信息传递给v时，节点u传递的信息由一个聚合函数控制，该函数由u与邻居的通信和关联历史参数化。

对于t时刻的任何事件，我们都会使用循环体系结构来更新事件中涉及的两个节点的嵌入。

对于节点v的第p个事件，我们将zv演化为

3.2.1.TEMPORALLY ATTENTIVE AGGREGATION

对于一个给定的节点，并不是所有的邻居都是一致重要的，因此以某种加权的方式从每个邻居中捕获信息变得非常重要。在动态图中，变化的邻域结构和节点之间的交互活动随着时间的推移会影响每个邻居的重要性对一个节点的重要性，从而使注意力本身成为一个时间演化的量。此外，这个数量还依赖于相邻节点通过进化表示而产生的关联和通信的时间历史。

我们提出了一种新的基于时间点过程的注意机制，它利用时间信息来计算节点间结构边缘的注意系数。然后使用这些系数来计算嵌入传播所需的聚合量（hstruct）。

设A (t)∈Rn×n是图Gt在t时刻的邻接矩阵。设·S (t)∈Rn×n·是一个随机矩阵，捕获了在t时刻的成对顶点之间的强度。我们可以把S看作是一个选择矩阵，它诱导了一个节点的自然选择过程——它会倾向于与它想要与之关联或最近关联的其他节点进行更多的通信。

为了正式地捕捉不同邻居的影响差异，我们提出了一种新的基于条件强度的注意层，它利用矩阵S来诱导一种共享注意机制来计算邻域上的注意系数。

具体来说，我们对给定的节点u进行局部注意，并计算与节点u的1跳邻域i的系数为：

其中qui表示t时刻邻居i的注意权重，因此它是一个时间演化的量。

然后利用这些注意系数计算节点u的聚合信息hu, struct（t¯），采用跨邻居的参与聚合机制如下:


zi（t¯）∈Rd是节点i的最新嵌入。

Connection to Neural Attention over Graphs
我们的模型的关键创新是通过一个基于点过程的时间量S来参数化注意机制，该时间量S正在进化，并驱动每个邻居对给定节点的影响。

Construction and Update of S
我们构造了一个单一的随机矩阵S（在前面一节中用于参数化注意力）来捕获复杂的时间信息。
在初始时间点t = t0，我们直接从A（t0）构造S（t0）。具体来说，对于给定的节点v，我们将相应的行向量Sv（t0）的元素初始化为： Svu（t0）= 0 if（v = u或Avu（t0）= 0）和Svu（t0）= 1 |Nv（t0）|如果Nv（t0）= {u： Auv（t0）= 1}。

注意，S是结构时间注意的参数，这意味着时间注意只应用于节点的结构邻域。因此，S的值只在两种情况下被更新/激活：
a)当前事件是已经有结构边缘的节点之间的交互作用（Auv (t) = 1和k = 1）。
b)当前事件是一个关联事件（k = 0）。
每当一个涉及u的事件发生时，这种注意力就会以以下方式发生变化：
对于案例(a)，相应的S条目的注意力值就会使用该事件的强度进行更新。
对于情况(b)，重复与(a)相同，但随着邻域大小的增加，调整与其他邻居的背景注意。
具体间算法1：

5.EXPERIMENTS

5.1.DATASETS

Social Evolution Dataset: 节点： 83，初始关联： 376，最终关联： 791，通信： 2016339，聚类系数： 0.548
Github Dataset: #节点： 12328，#初始关联： 70640，#最终关联： 166565，#通信系数： 604649，聚类系数： 0.087

5.2.TASKS AND METRICS

我们通过评估动态链接预测任务和事件时间预测任务的模型来研究DyRep的有效性：

5.3.BASELINES

5.5.EXPERIMENTAL RESULTS

Communication Event Prediction Performance(a-b)
Association Event Prediction Performance(c-d)

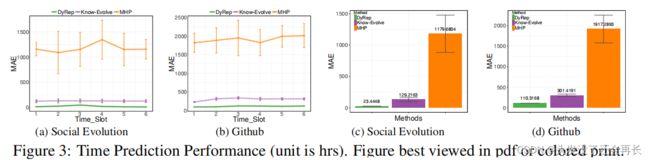
Time Prediction Performance

Qualitative Performance

6.CONCLUSION

作者介绍了一种新的动态图建模框架，通过将表示学习作为连接拓扑演化和节点交互的动态过程的潜在中介过程，有效地学习节点表示。
作者提出了一个由时间注意表示网络参数化的深度时间点过程模型，该模型建模了这些复杂且非线性演化的动态过程，并学习将图上的结构-时间信息编码为低维表示。作为框架的一部分，还提出了一种新的基于时间点过程的注意机制，该机制可以基于图中通信和关联事件的历史来参与邻域。